[CS224W] Lecture 4

Person

Title

Link Analysis: PageRank, RWR, MF

비고

4.1 PageRank

웹은 그래프라 생각할 수 있습니다. 웹페이지는 node, 하이퍼링크는 edges라고 둘 수 있습니다.

하지만 웹은 하이퍼링크를 통해 페이지가 서로 단방향으로 연결되어 있기 때문에 directed graph입니다.

모든 웹페이지가 중요한 페이지는 아니기 때문에 페이지끼리 순위를 매겨야 합니다.

이를 위해 link analysis로 node들의 중요도를 측정한 방법이 다음과 같이 3가지 종류가 있습니다.

1.

PageRank

2.

Personalized PageRank (PPR)

3.

Random Walk with Restarts

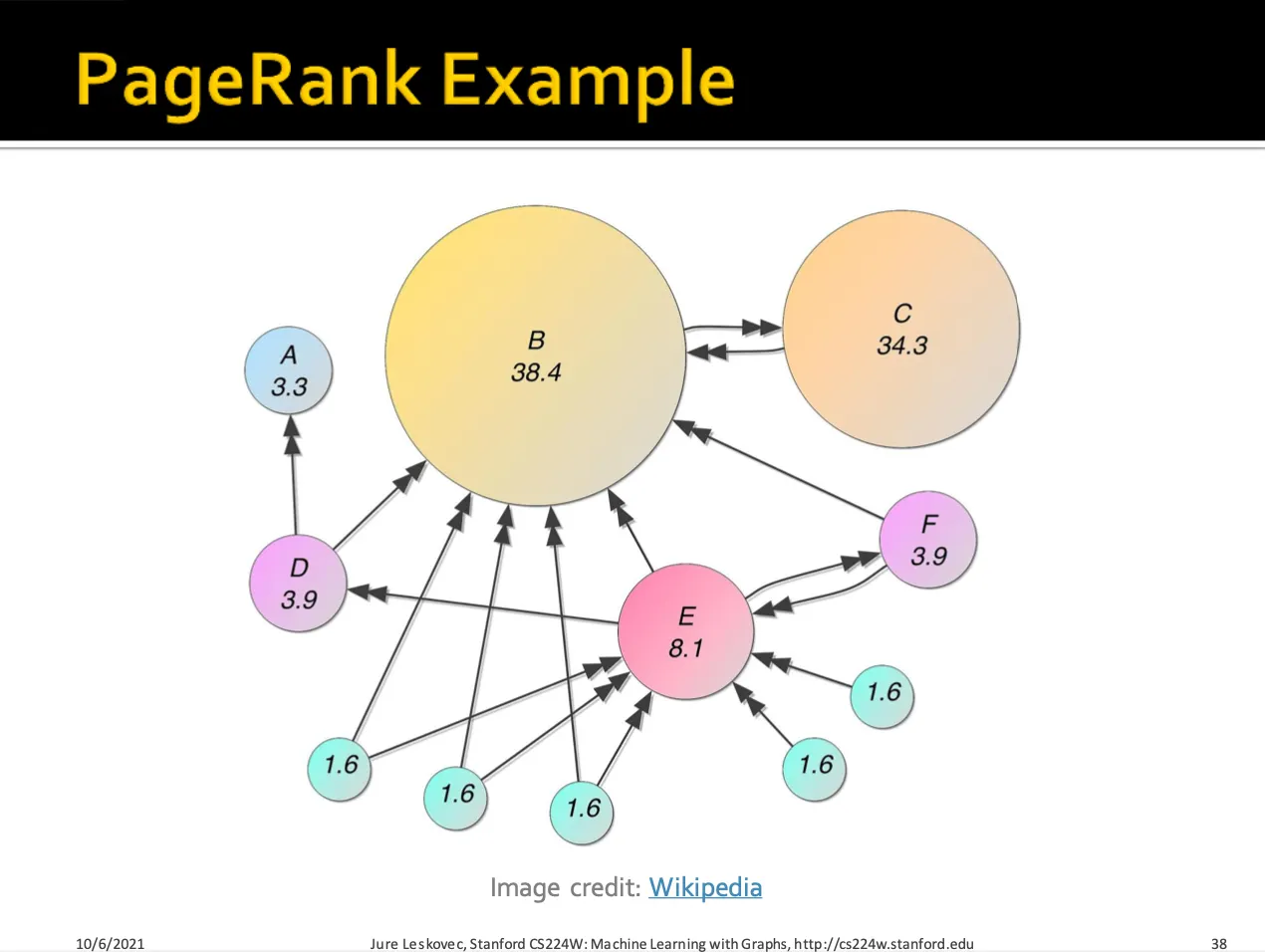
PageRank는 각각의 source node들의 rank(importance) 를 out-link 의 개수에 나눈 값들을 link의 rank로 두고, target node에 대해서는 이 rank들을 더합니다.

d_i

가

i

의 out-link 개수,

r_i

가 node

i

의 rank 일 때, node

j

의 rank는 다음과 같습니다.

r_j = \sum_{i \rightarrow j}^{} \frac{r_i}{d_i}

d_i

를 값으로 가지는 행렬인

M

(column stochastic matrix)를 만들 수 있습니다.

node i에서 node j가 연결되어 있다면

M_{ji} = \frac{1}{d_i}

로 나타냅니다.

이때

M\cdot r

은 pagerank를 한 번 계산한 값이며, 각각의 원소가 다시

r

를 나타내므로,

r = M \cdot r

이란 식으로 나타낼 수 있습니다.

또한

1\cdot r = M \cdot r

이므로 (

\lambda \cdot c = A \cdot c)

r

은

M

에 대한 principle eigen vector (eigen value가 1인)라 할 수 있습니다.

4.2 PageRank : How to Solve?

r

를 계산하는 방법으로 power iteration method가 있습니다.

처음에 모든 node들을 똑같은 확률로 initialize하고 계속

M

를 곱하여

r^t

가 수렴할 때까지 반복하는 방법입니다.

power iteration을 통해

r_y

,

r_a

,

r_m

을 구한 모습입니다.

하지만, 이렇게 반복해서 계산했을 때 수렴한다는 보장이 없으며, 수렴했을 때 rank 값들이 원하는 값이 아닐 수 있습니다.

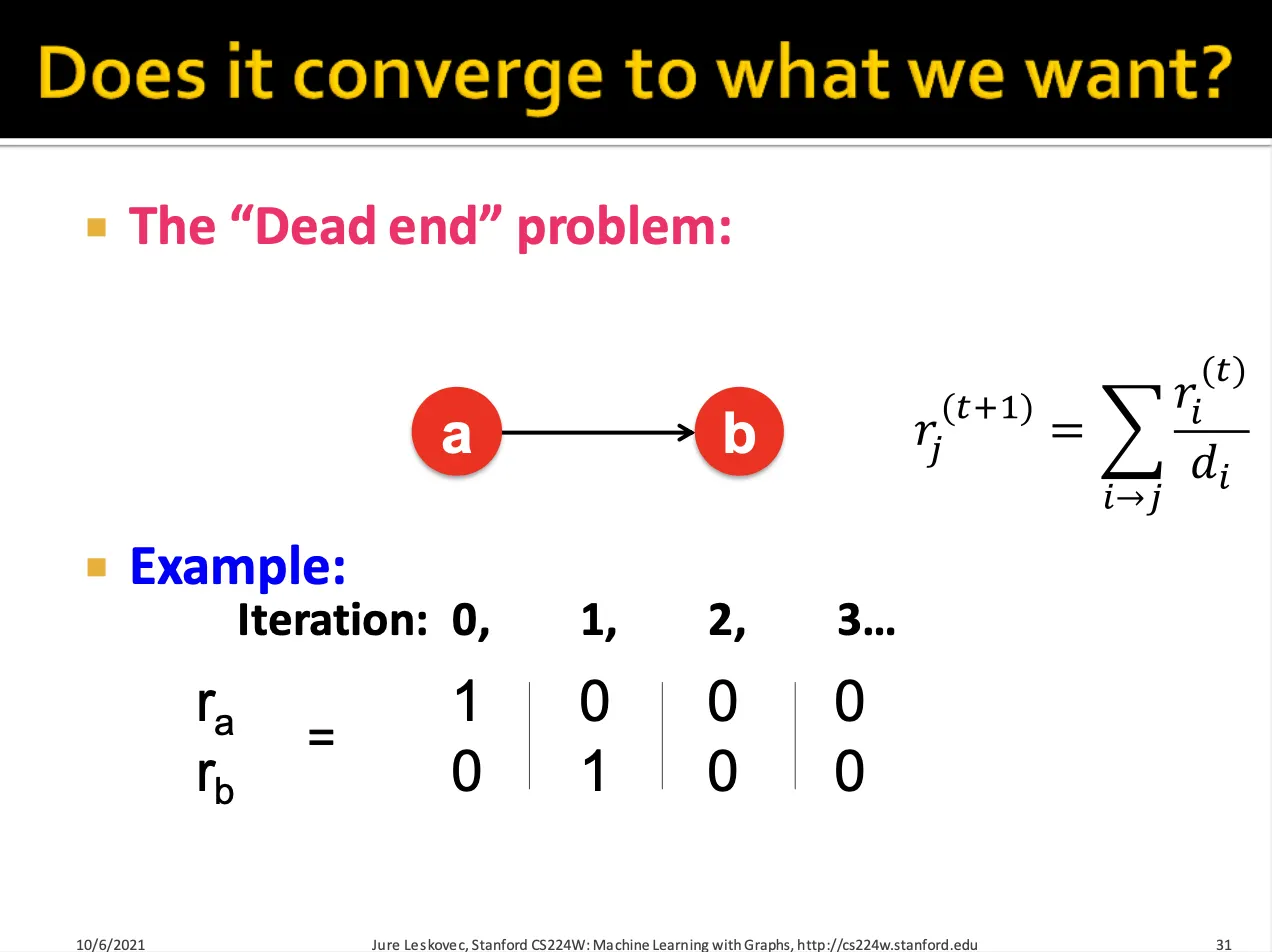
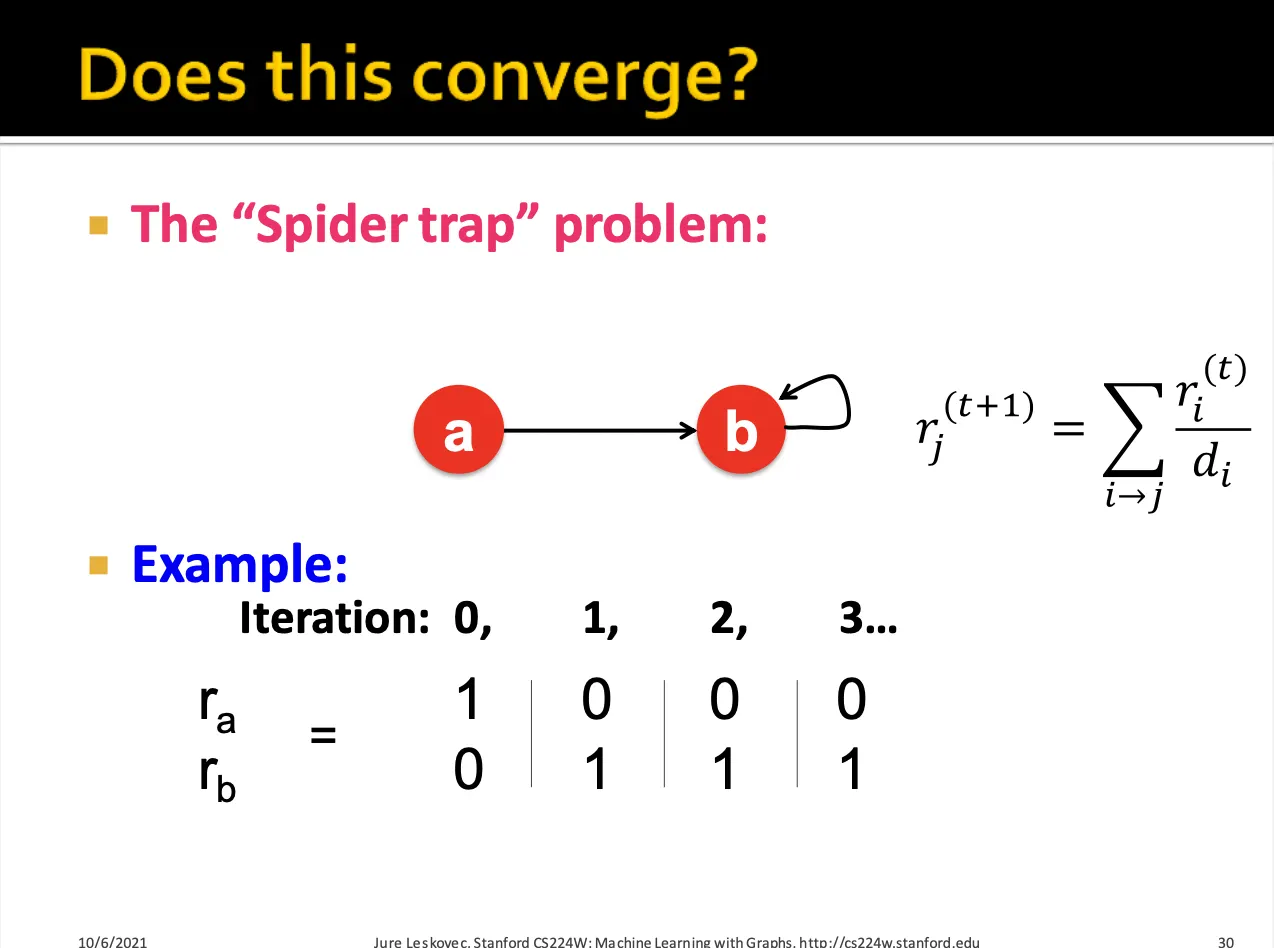
Dead ends와 Spider traps 라는 두가지 문제점이 있습니다.

Dead end의 경우 out-link가 없는 node에 대해서 iteration을 반복하면 rank가 0으로 수렴할 수 있습니다.

Spider trap의 경우 out-link가 자기자신이므로 rank가 같은 값으로 유지되거나 계속 커지는 현상이 발생합니다.

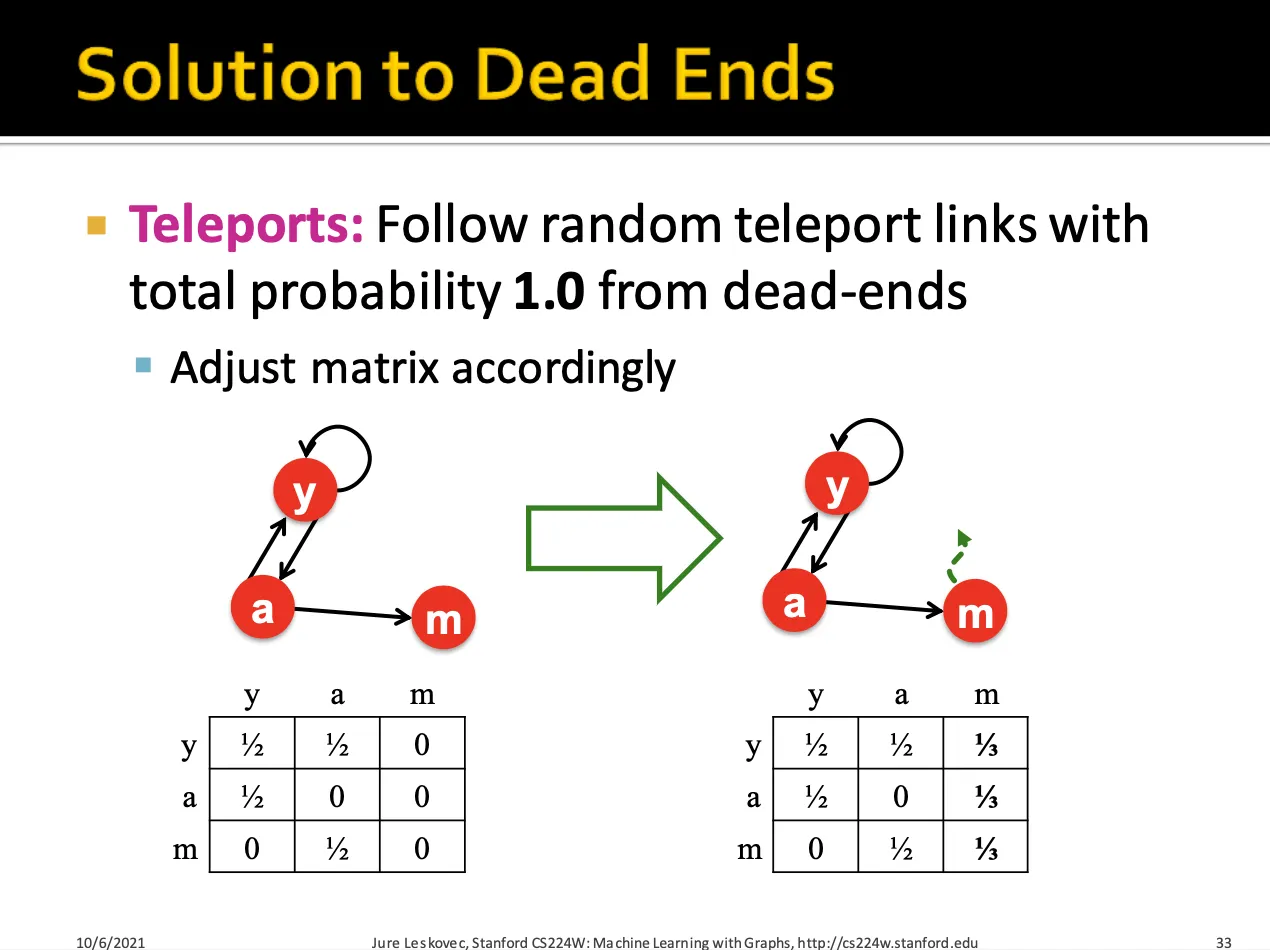
Dead Ends에 대한 해결방법으로는 dead-ends에 도달했을 때 일정 확률을 통해 다른 node로 teleport 할 수 있게 하는 것입니다.

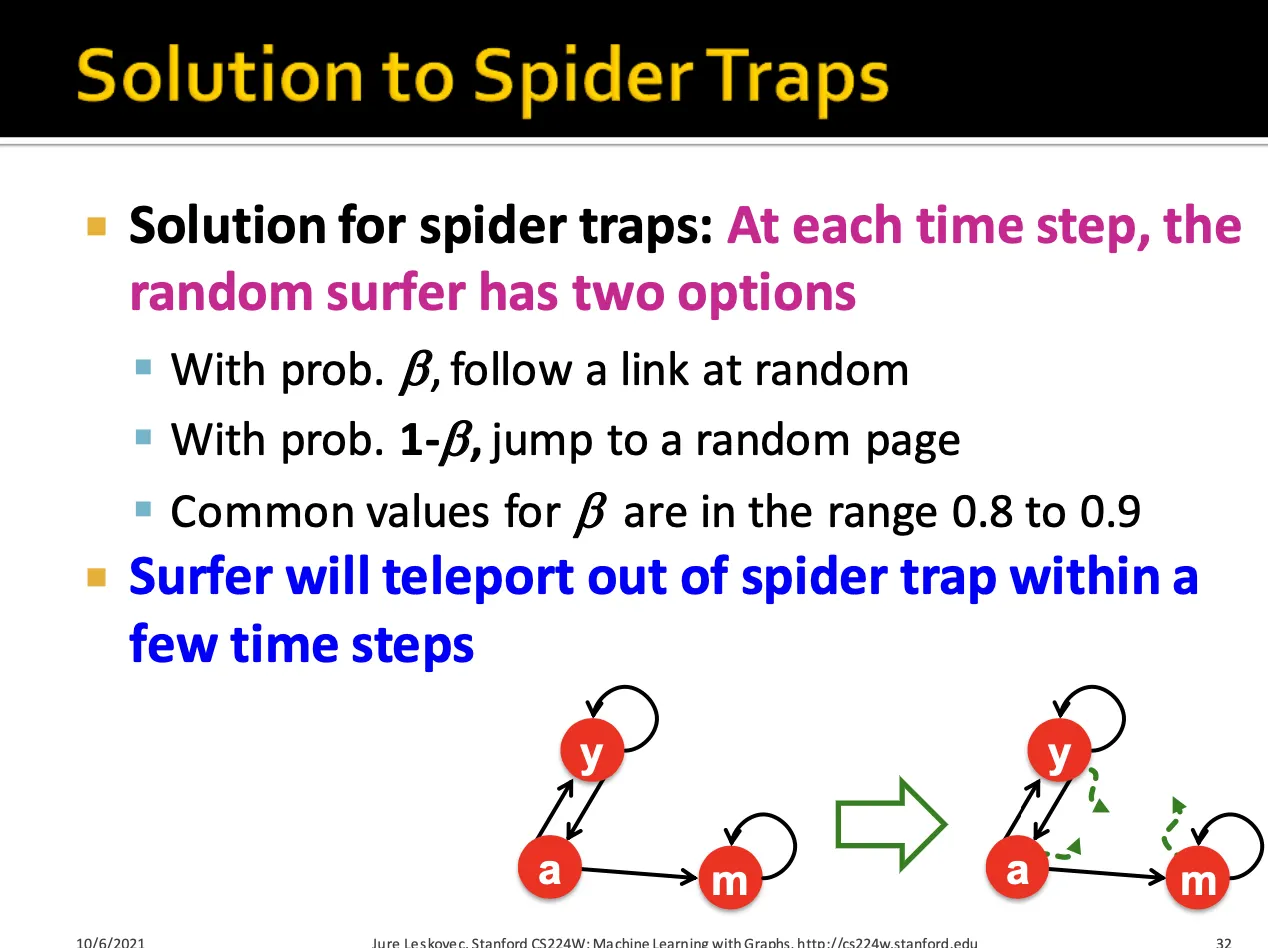
spider traps에 대한 해결방법 역시 각 node들에 대해서 특정 확률로 random jump를 하여 다른 node로 갈 수 있도록 하는 것입니다.

Random teleport을 통해 spider trap 또는 dead end 때문에 원하지 않는 rank로 수렴하는 것을 막을 수 있습니다.

식으로써 random teleport를 나타내면 위와 같습니다.

앞의 항은 random walk, 뒤쪽 항은 random jump라고 생각하면 됩니다.

만약 똑같은 확률로 random jump를 하는 것이 아니라 bias 된 확률로 random jump를 한다면, 이를 Personalized PageRank라 합니다.

4.3 Random Walk with Restarts

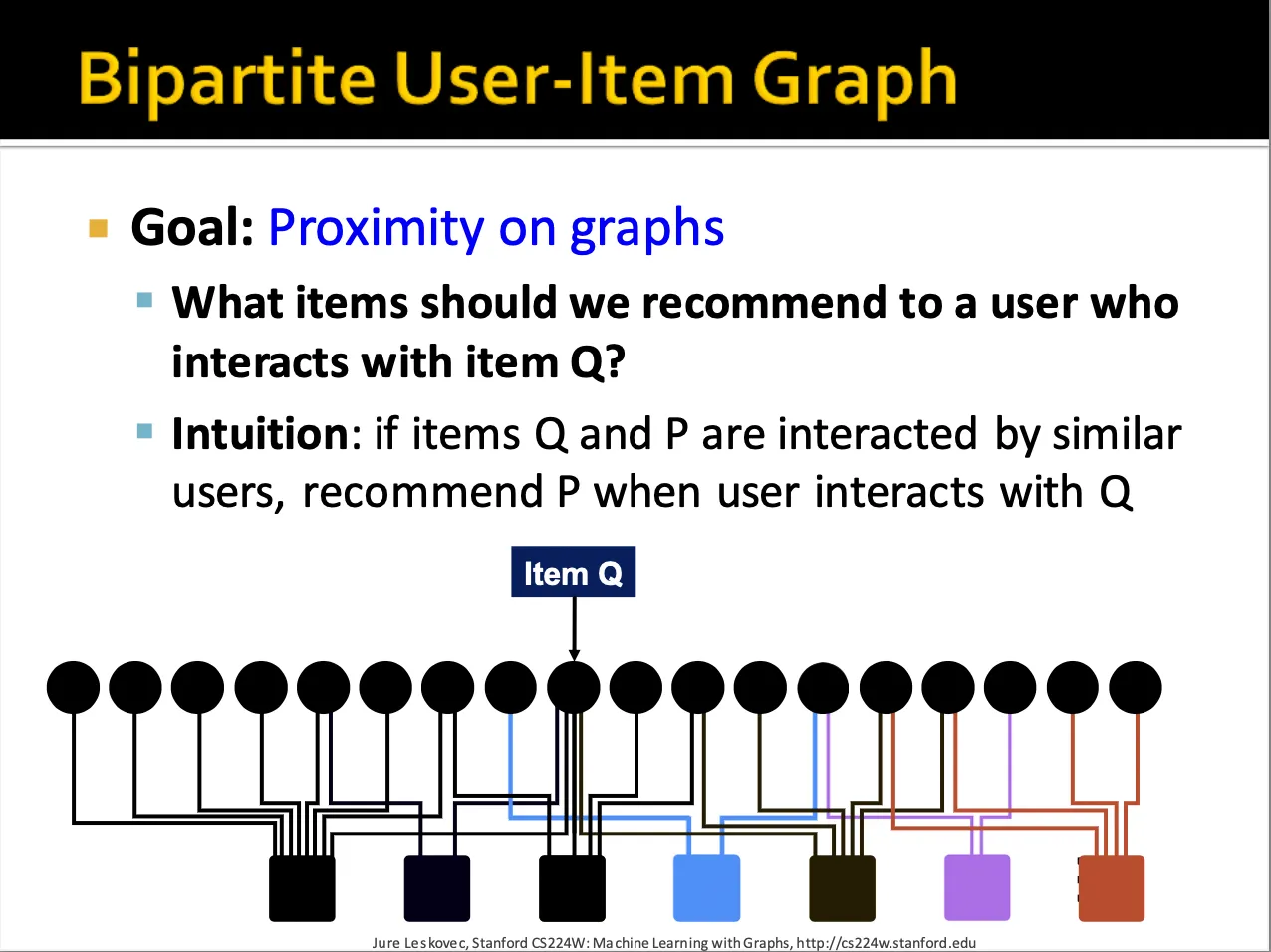
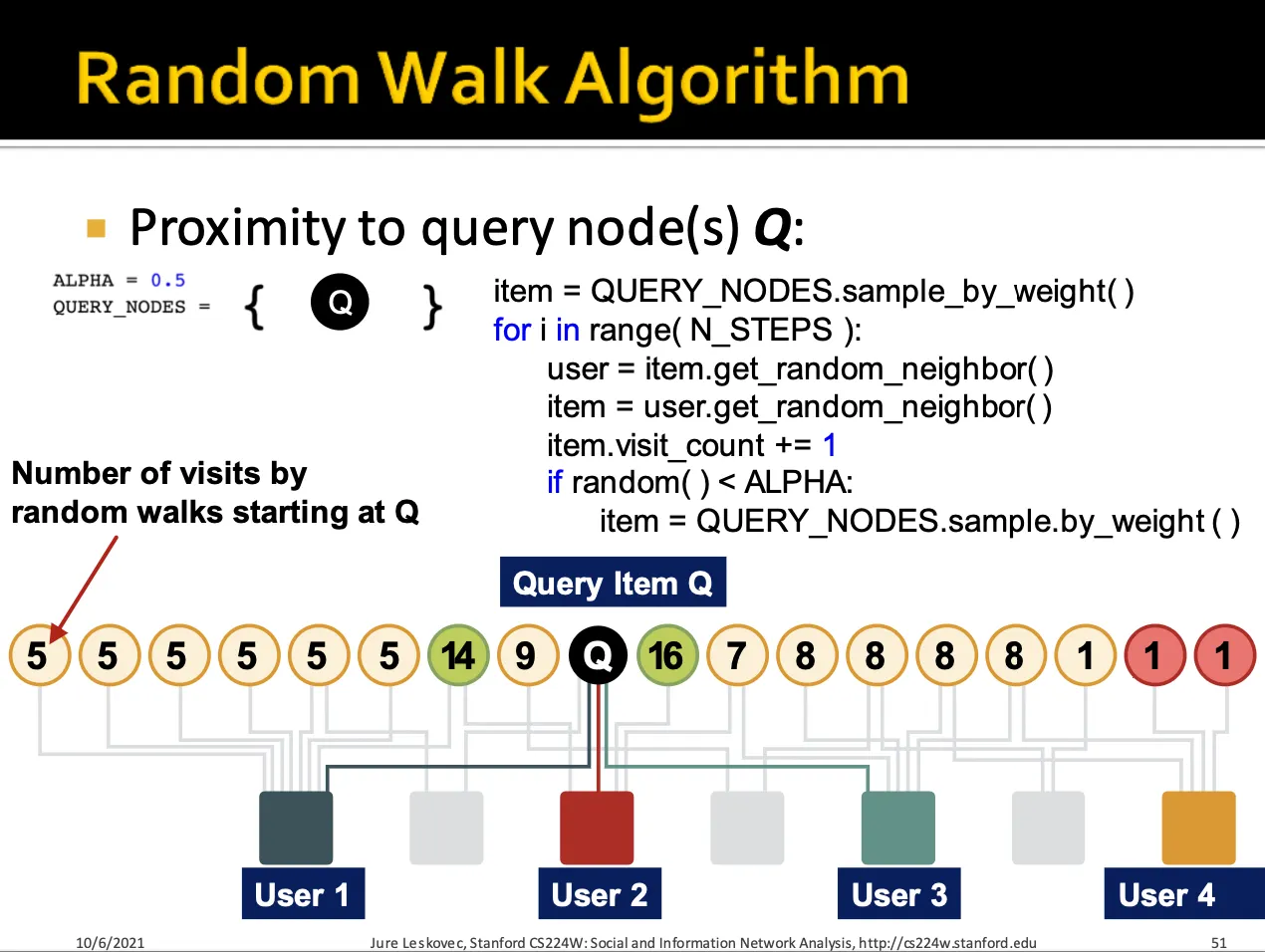
Bipartite graph에서 비슷한 interaction을 가진 item을 추천할 때 random walk 알고리즘을 사용합니다.

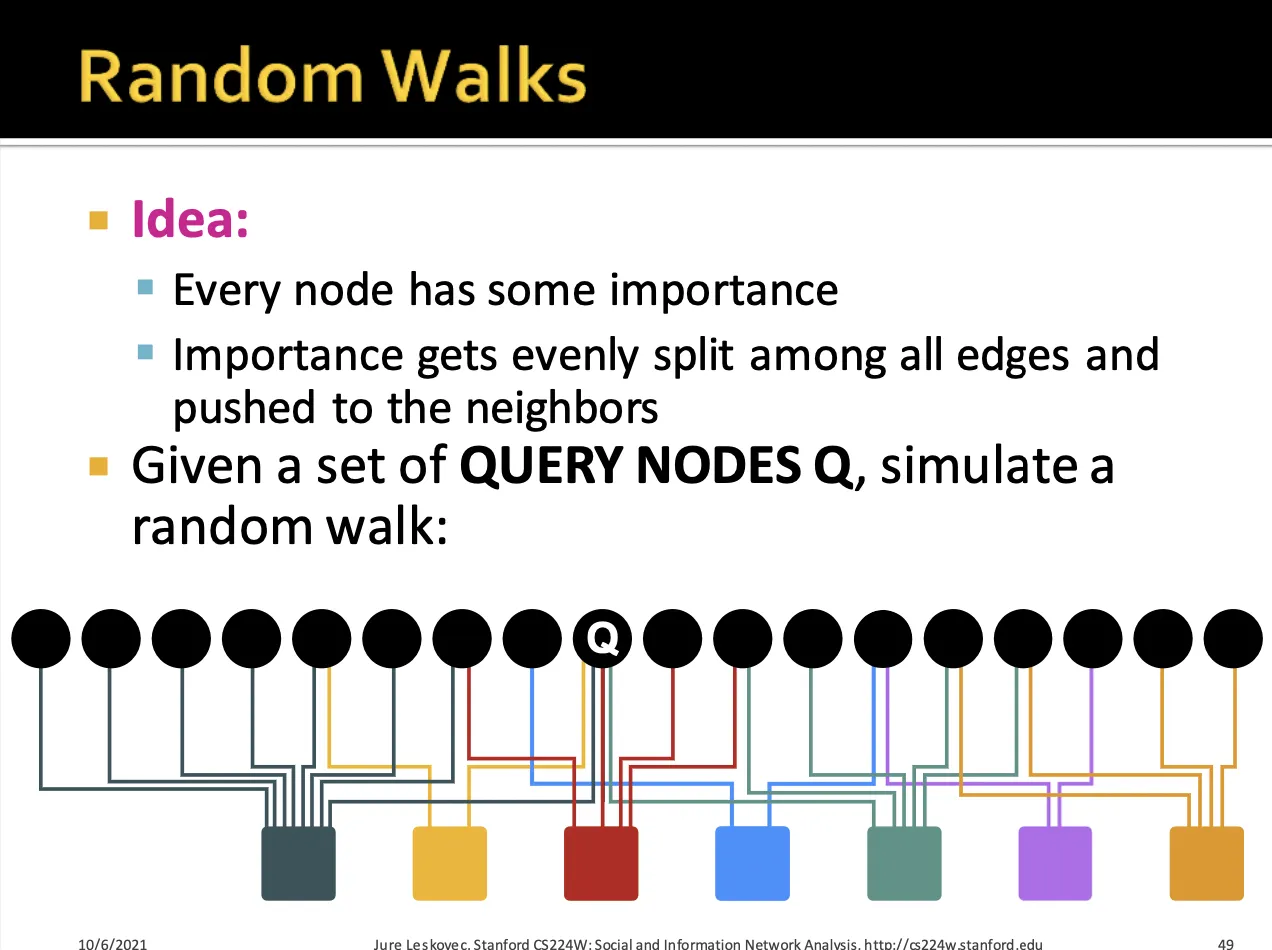
어떤 Query node Q가 있을 때, 이 node에서 random walk를 시작하게 됩니다.

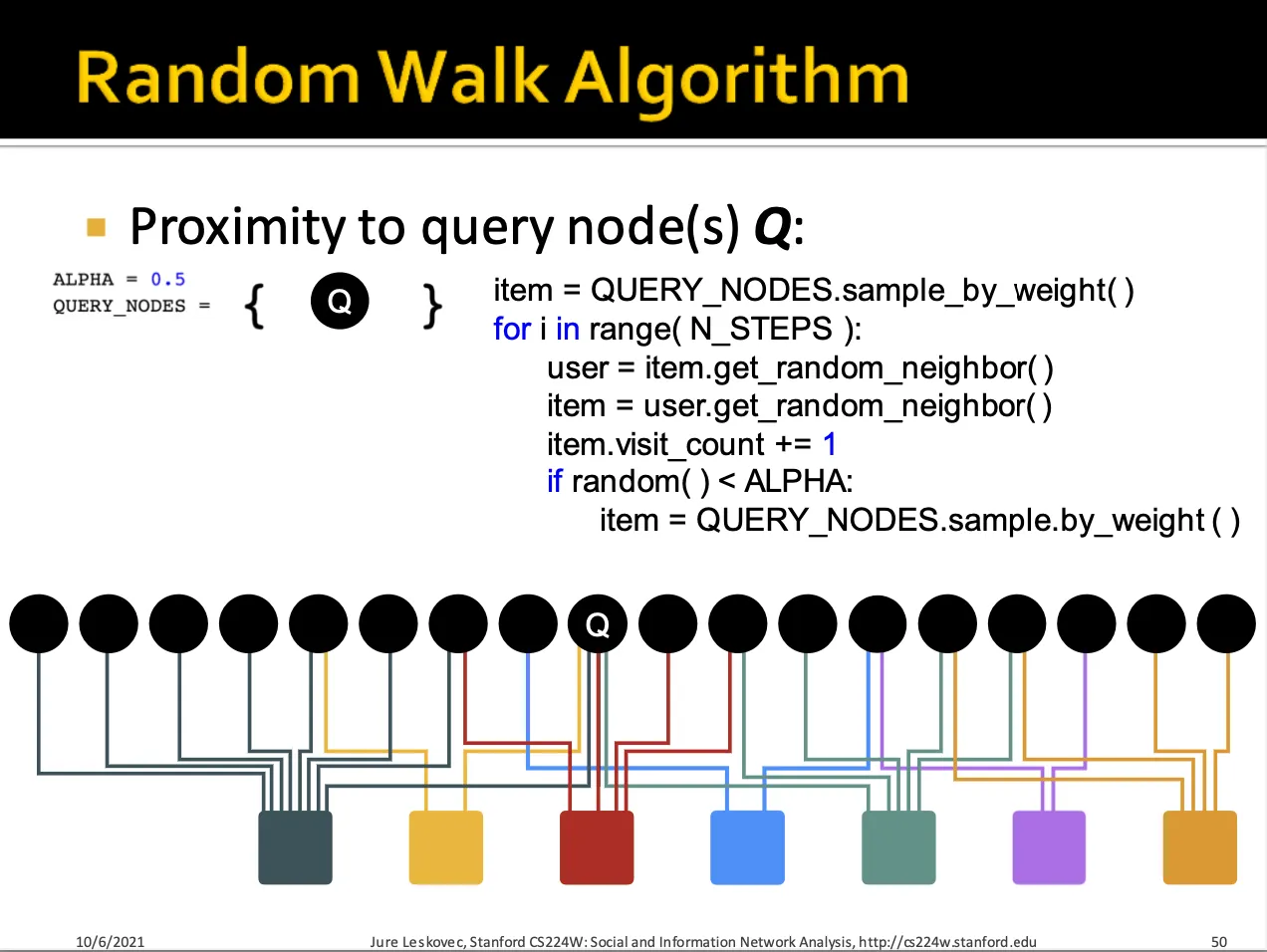
Random walk 알고리즘은 query node (item) 에서 시작하여 random user node를 거쳐 random item node에 방문하면, 해당 item node의 방문 횟수를 기록합니다.

또한 특정확률로 query node item에서 다시 random walk를 시작합니다.

이를 통해 각 item node에 대해서 방문 횟수를 구하게 되면 Query node Q와 가장 비슷한 item을 찾을 수 있습니다.

4.4 Matrix Factorization and Node Embeddings

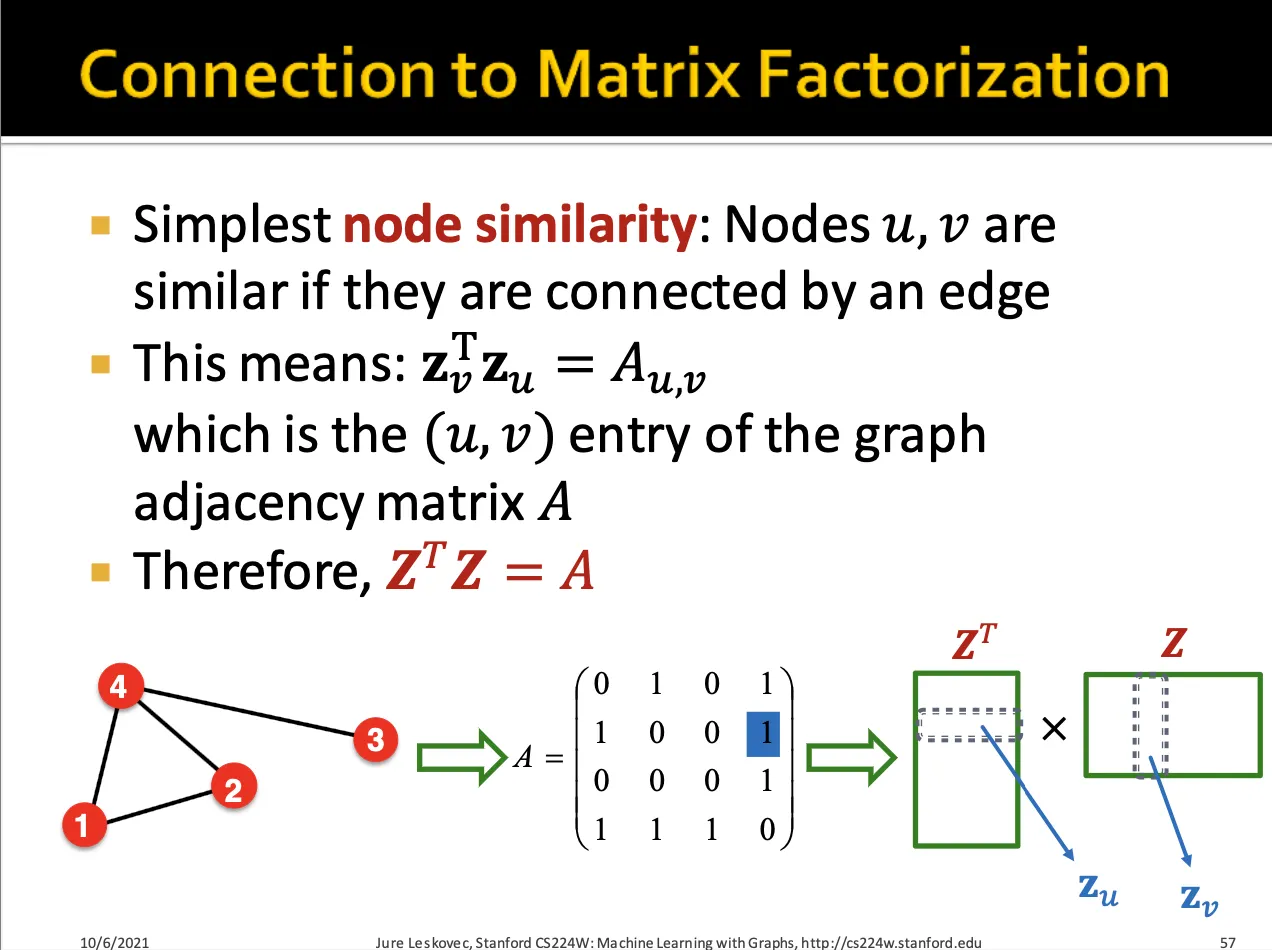
node embedding을 만들 때 만약

i

와

j

node가 서로 연결되어 있다면

A_{ij} = 1

이고

z_{i}^T \cdot z_{j} = 1

가 되도록

z_i , z_j

를 만들어야 합니다.

따라서 이상적으로는

A = Z^TZ

이고, objective function을 위와 같이 세울 수 있습니다.

DeepWalk과 Node2Vec 알고리즘을 통해서도 node similarity를 계산할 수 있습니다.

→ 무슨 내용인지 모르겠습니다…

matrix factorization과 random walk를 통해 node embedding을 하게 되면 생기는 세가지 한계점이 있습니다.

1.

새롭게 node가 추가되면 그래프 전체를 다시 학습해야 합니다.

2.

그래프의 structural similarity를 알 수 없습니다.

3.

node, edge의 feature들을 추가로 이용해 다른 목적으로 사용할 수 없습니다.

a.

protein-protein interaction graph에서 protein property를 feature vector로 사용할 수 없음