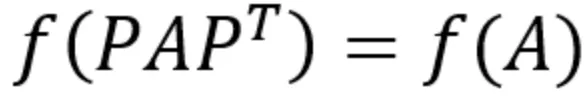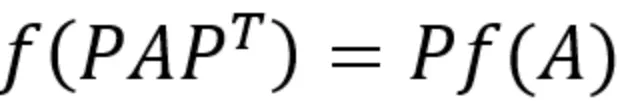Recap
•
Similarity function의 필요성
◦
원래 그래프에서 가까운 두 node의 embedding도 비슷하게 되었는지 확인해야 함
◦
비슷한 embedding이라는 것은 내적으로 확인, similar한지 어떻게 확인할 것인지 결정 필요
•
Shallow encoder의 단점
◦
많은 수의 파라미터 필요
◦
Transductive
◦
Node feature 적용 불가
Deep Learning for Graphs
•
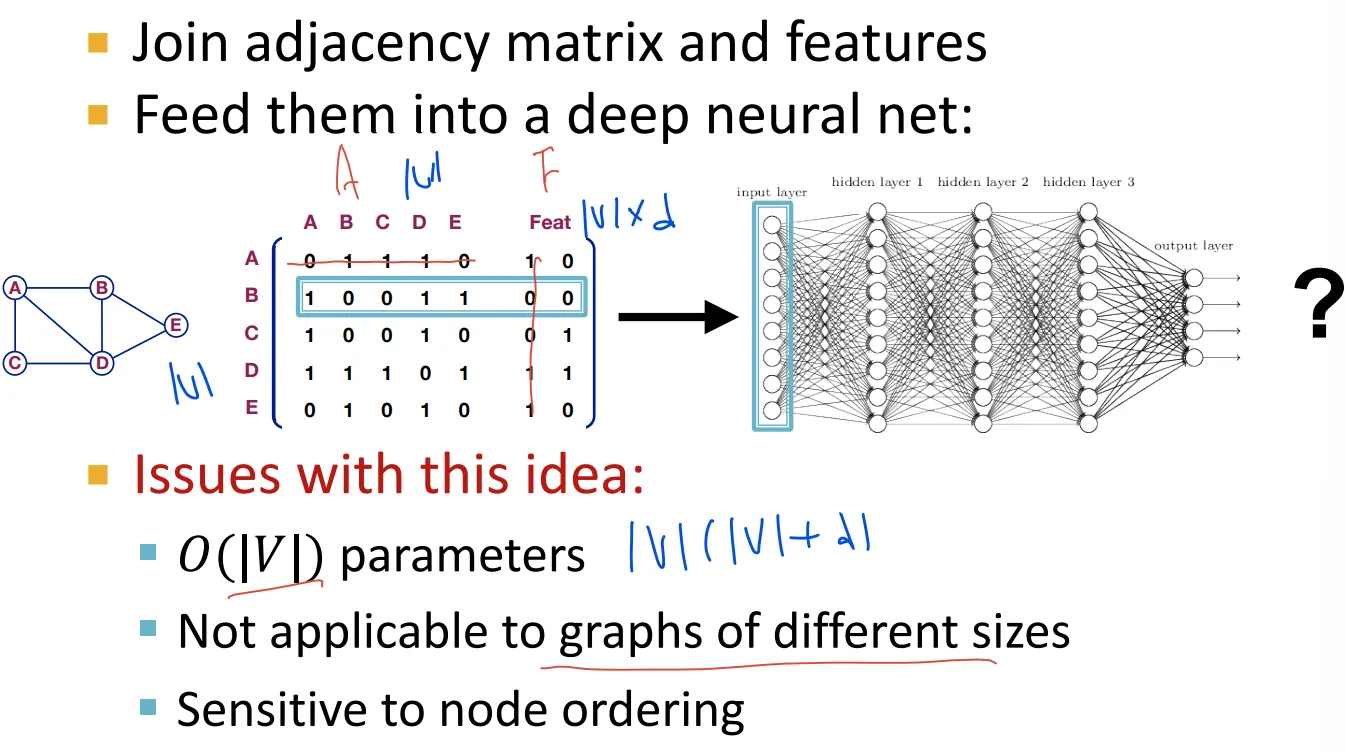
Naive approach
◦
Adjacency matrix랑 feature를 이어서 DNN에 넣으면 안될까?
◦
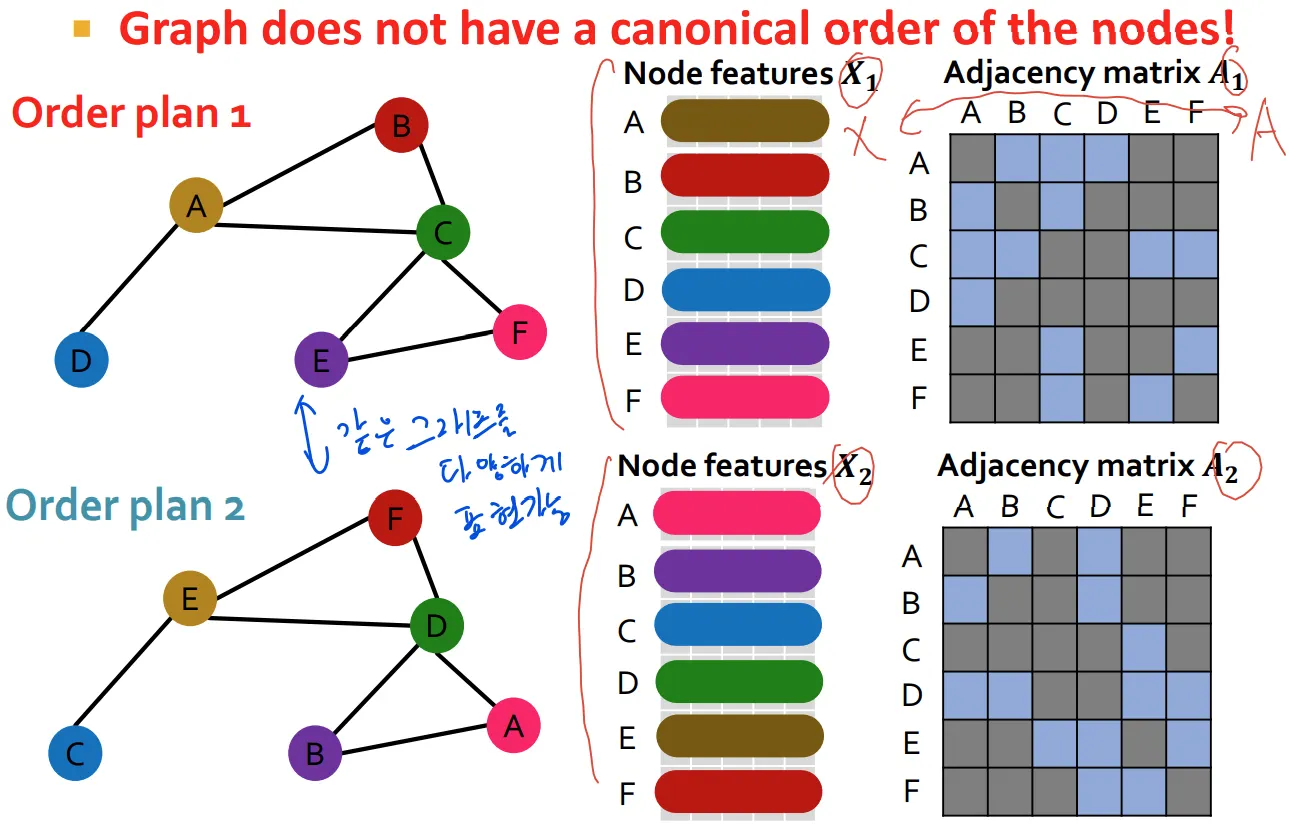
서로 다른 순서의 표현형에 대해 다르게 나타나므로 안됨
•
Permutation invariance and permutation equivariant
◦
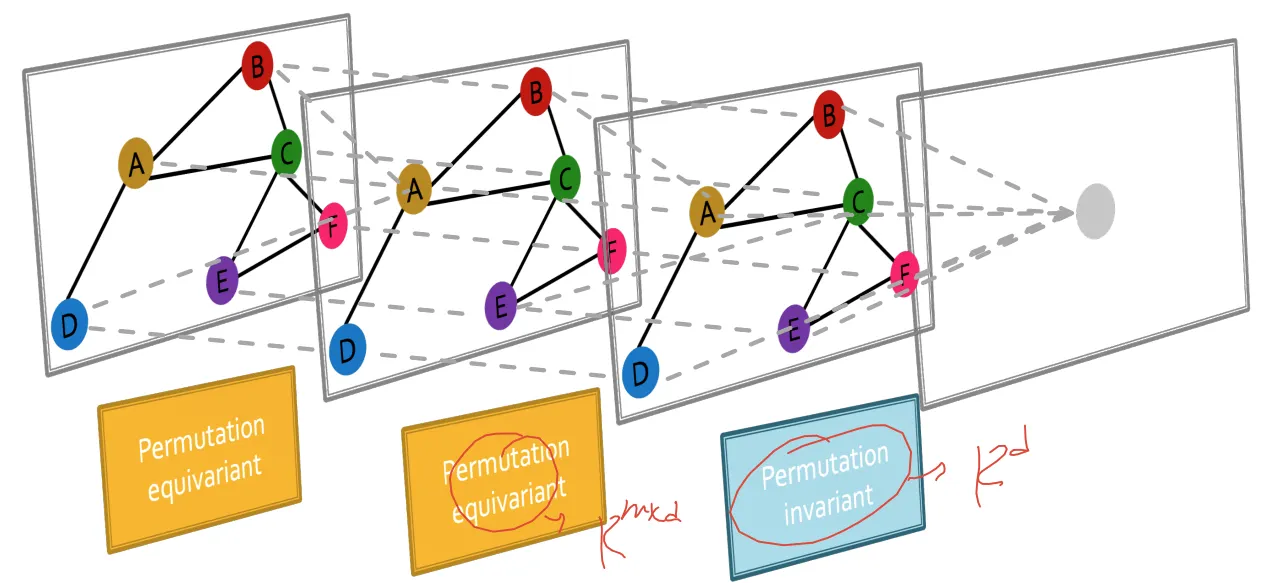
Order plan 1으로 가든, Order plan 2로 가든 함수의 결과가 같아야 하고, 이것이 permutation invariant
◦
Permutation 결과에 따라서 output의 결과도 같이 바뀌면 permutation equivariance → aggregation 전 까지는 permutation equivariance 해야함
◦
Permutation invariant
◦
Permutation equivariant
•
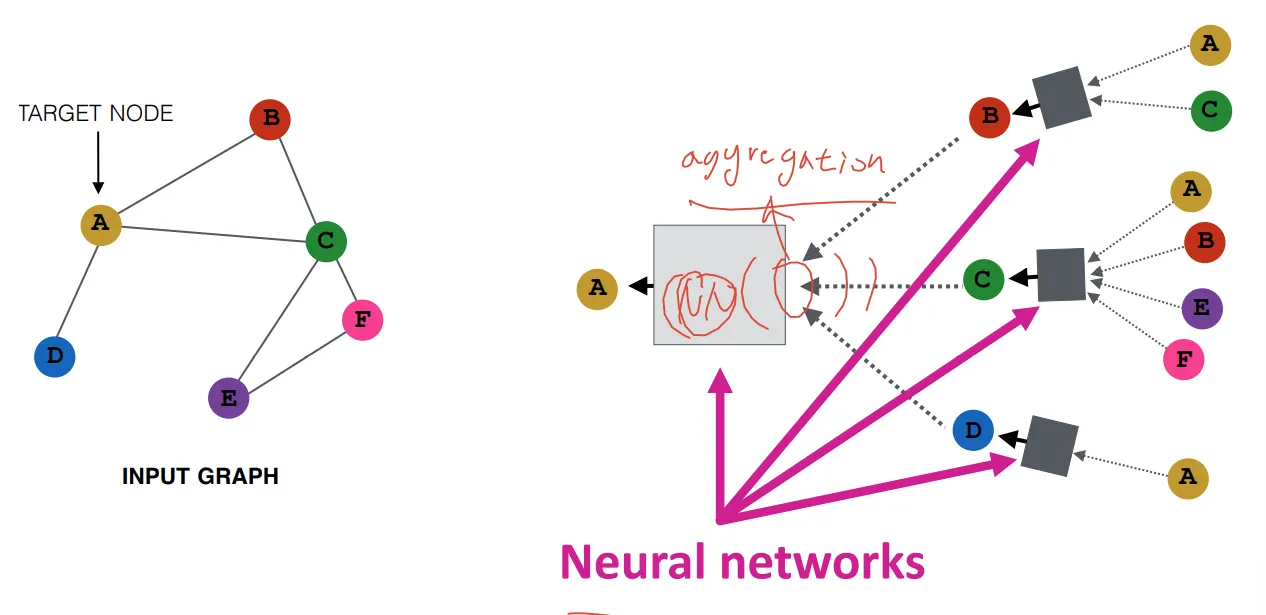
Neighborhood aggregation
◦
Neighborhood의 정보를 모으고, 모은 정보를 NN에 통과시킴
◦
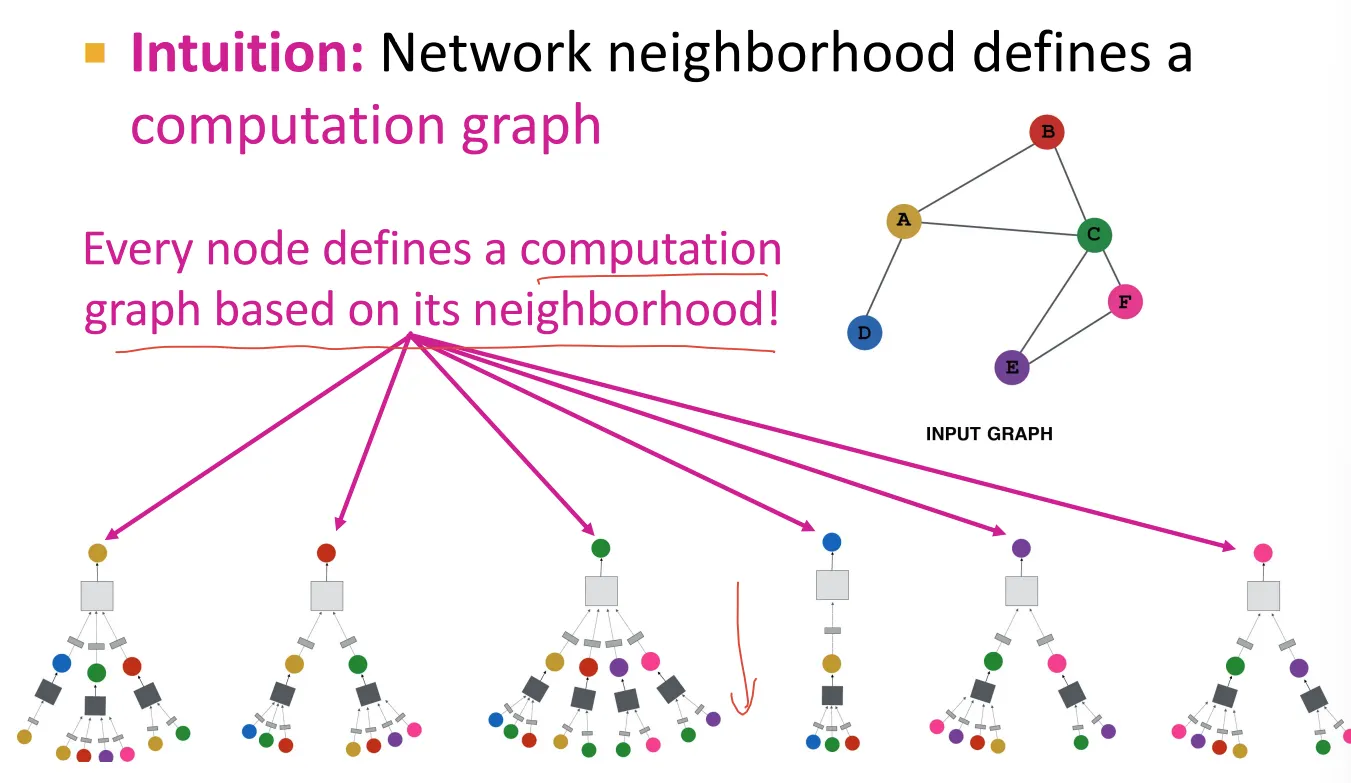
이런 형태는 각 node에 대해 computation graph를 만듦
◦
Computational graph가 한층 깊어질 때마다 1-hop connection 더 표현
•
Mathematical expression
◦
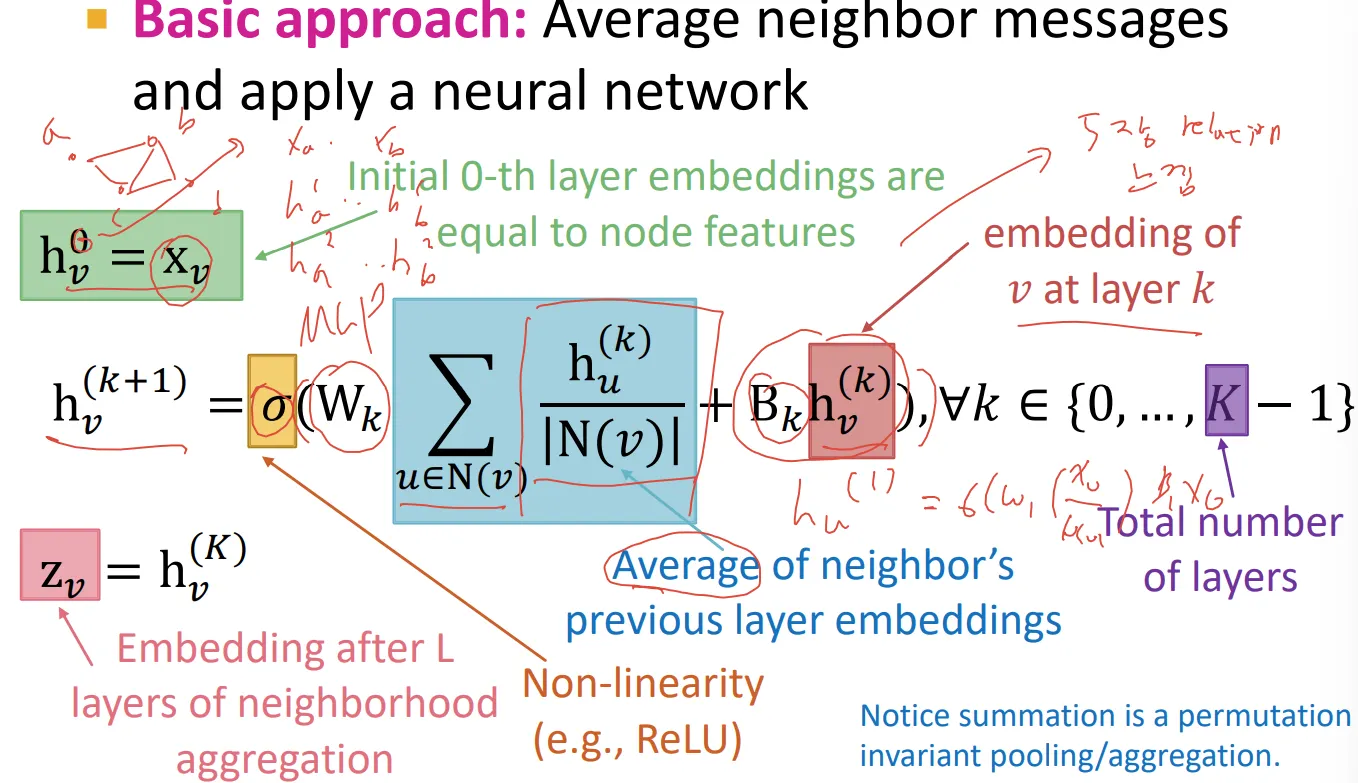
개별 node에 대한 식은 아래와 같음. 내 주위 node 정보 합쳐서 MLP 통과 시키고, 내 자체 정보도 MLP 통과 시킨 이후에 더하고 non-linear function에 넣겠다는 의미
◦
이때 행렬 와 가 학습 대상이며, k번째 layer에 대해서 globaly share됨
◦
행렬 형태로 다시 바꿔서 표현하면, normalize하는 부분까지 포함해서 아래와 같이 표현 가능
•
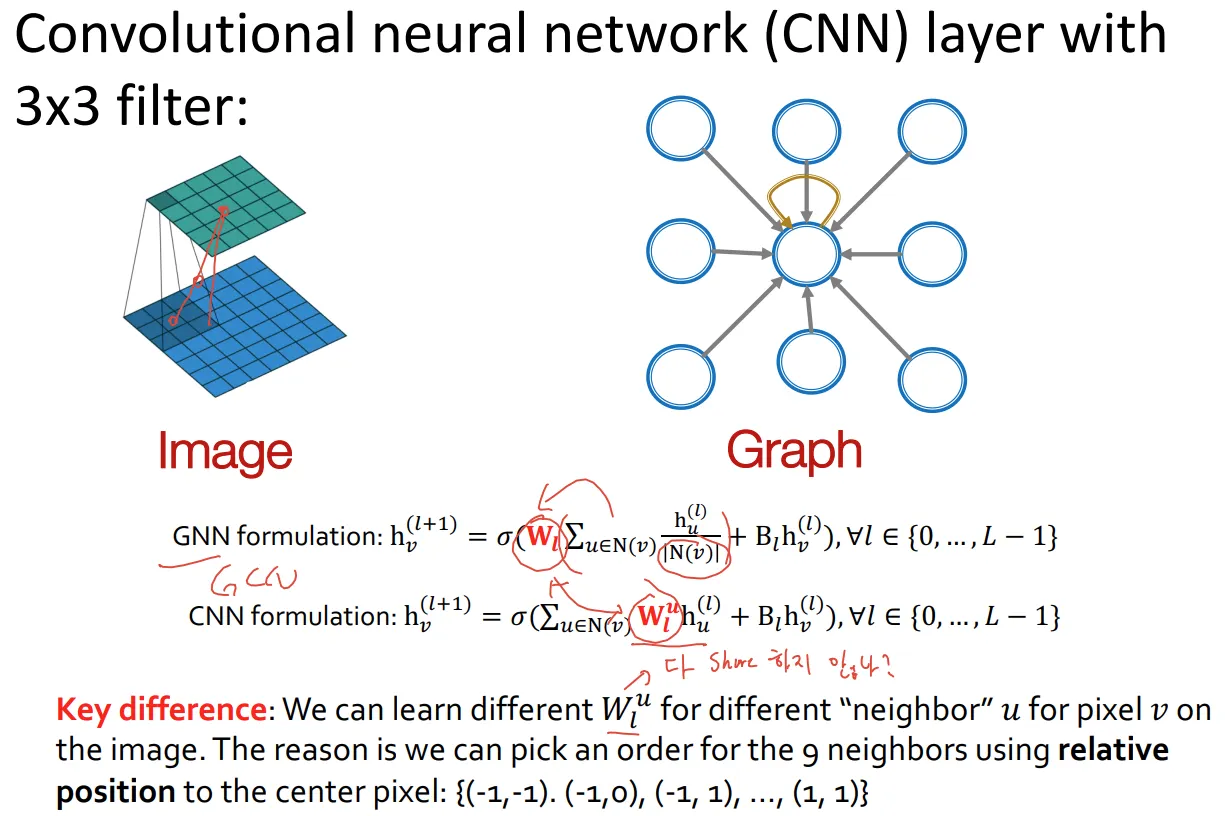
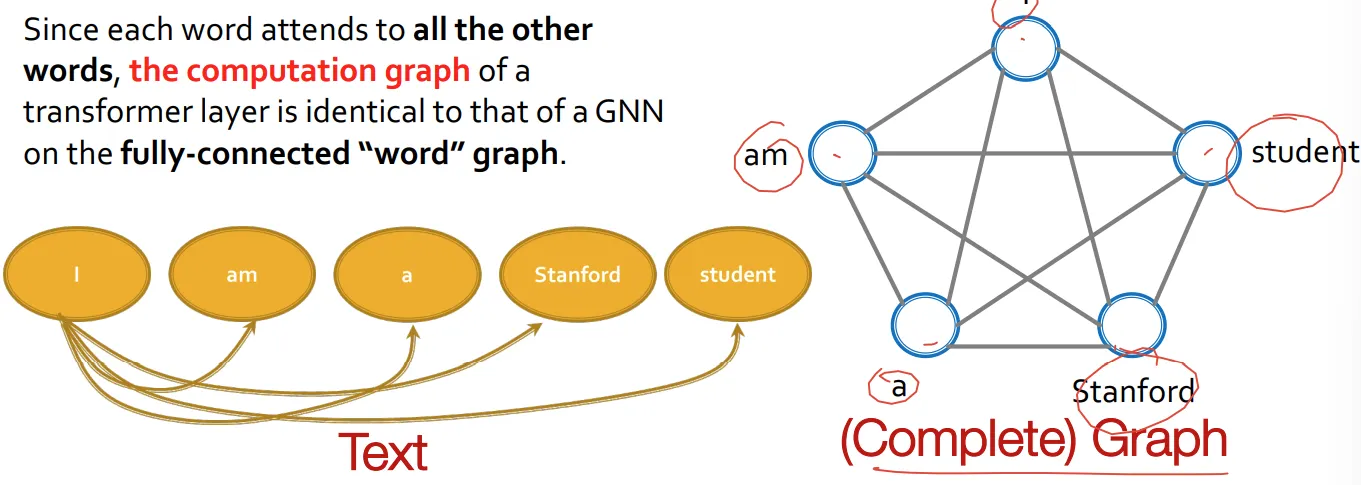
GNN subsume CNN and Transformer
◦
사실 엄밀히 말하면 완전 subsume은 아님
◦
단어들 사이의 관계를 본다는 점에서 attention과 유사