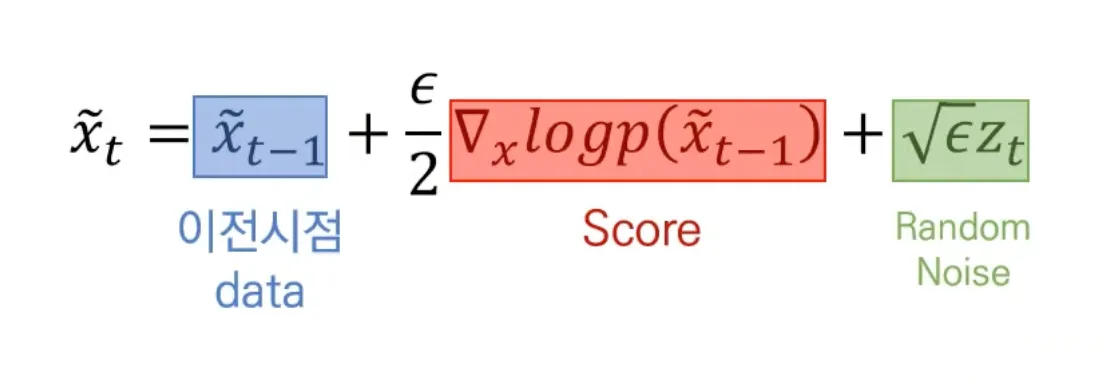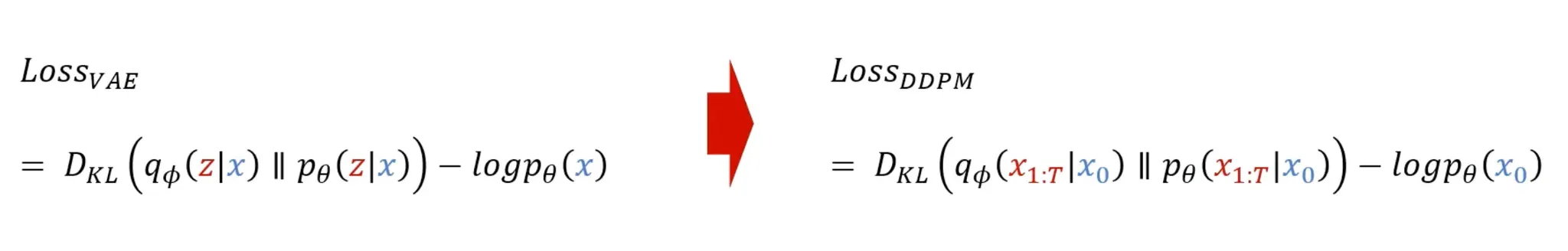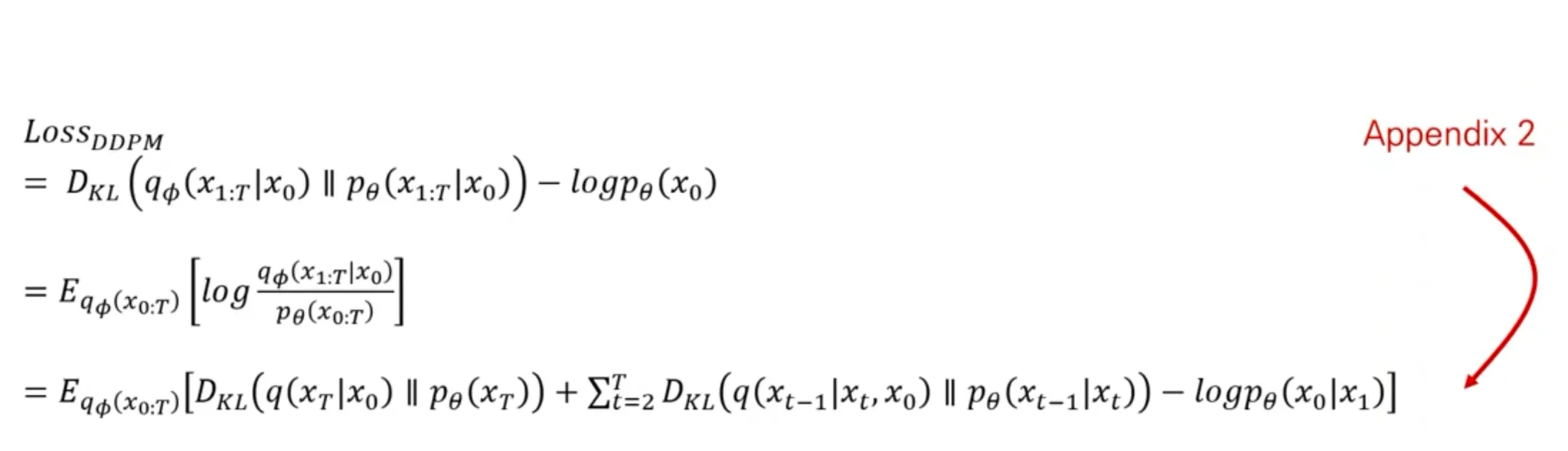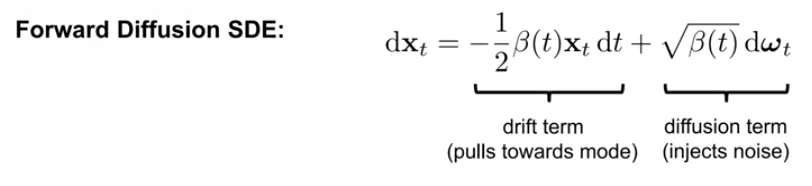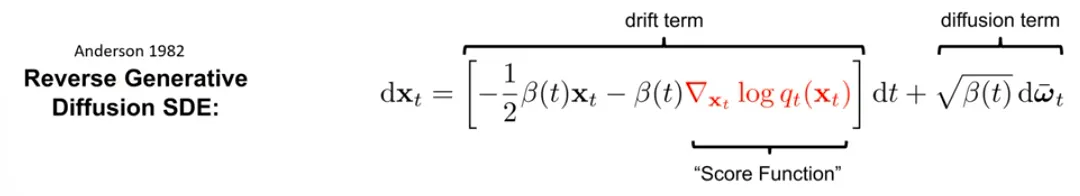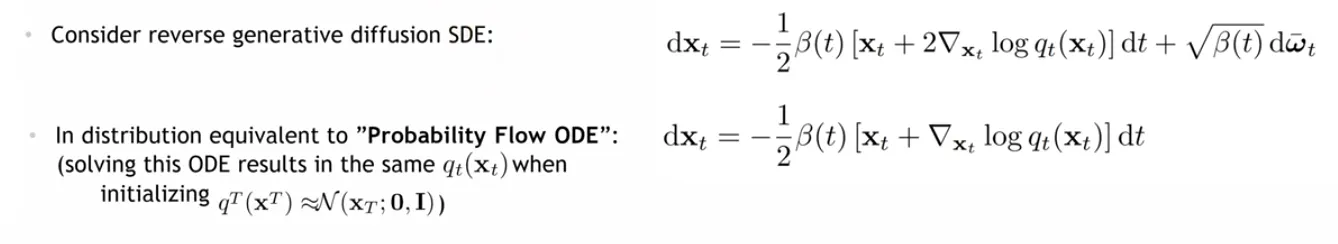Introduction to Diffusion Models

Introduction

높은 해상도와 다양성을 지닌 generative framework인 Diffusion model에 대해 분석하고 소개하는 페이지입니다.

여러 Reference를 참고하여 직접 작성하였습니다.

Table of Contents

Summary

•

Score based Generative Models (NCSN)

Random noise에서 시작해 score 값을 따라 높은 확률값이 있는 공간에서 data를 생성하는 것.

•

Diffusion Models (DDPM)

Noise를 제거하는 과정을 학습해 random noise로부터 data 생성

•

Score-based Generative Modeling with SDEs

SDE라는 framework으로 NCSN과 DDPM을 통합함.

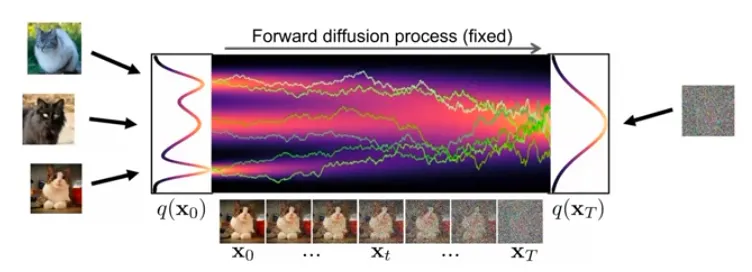
What is Diffusion?

•

Diffusion destroys structure!

•

최초의 연기 (smoke)는 점차 uniform 하게 분포할 것이다.

•

이를 역으로 추론해보면 최초의 연기를 알 수 있지 않을까?

•

Physical intuition: 짧은 sequence 안에서의 forward diffusion, reverse diffusion 모두 Gaussian 일 수 있다.

Score-based Generative Models

•

Generative modeling by estimating gradients of the data distribution (Song et al. 2019)

•

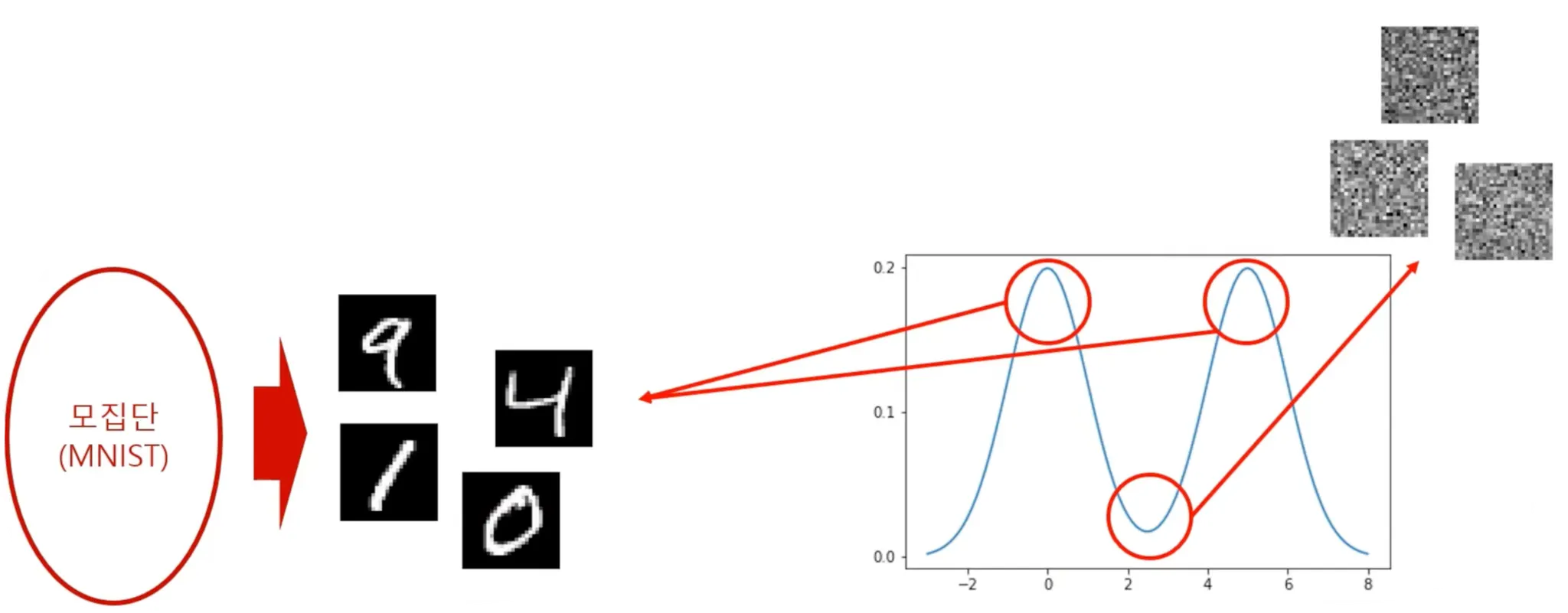
데이터는 모집단에서 샘플링된다.

•

샘플링된 데이터는 데이터 분포에서 높은 확률값을 갖는 데이터임. 낮은 확률값을 갖는 데이터는 noise 형태일 것.

•

Generation overview

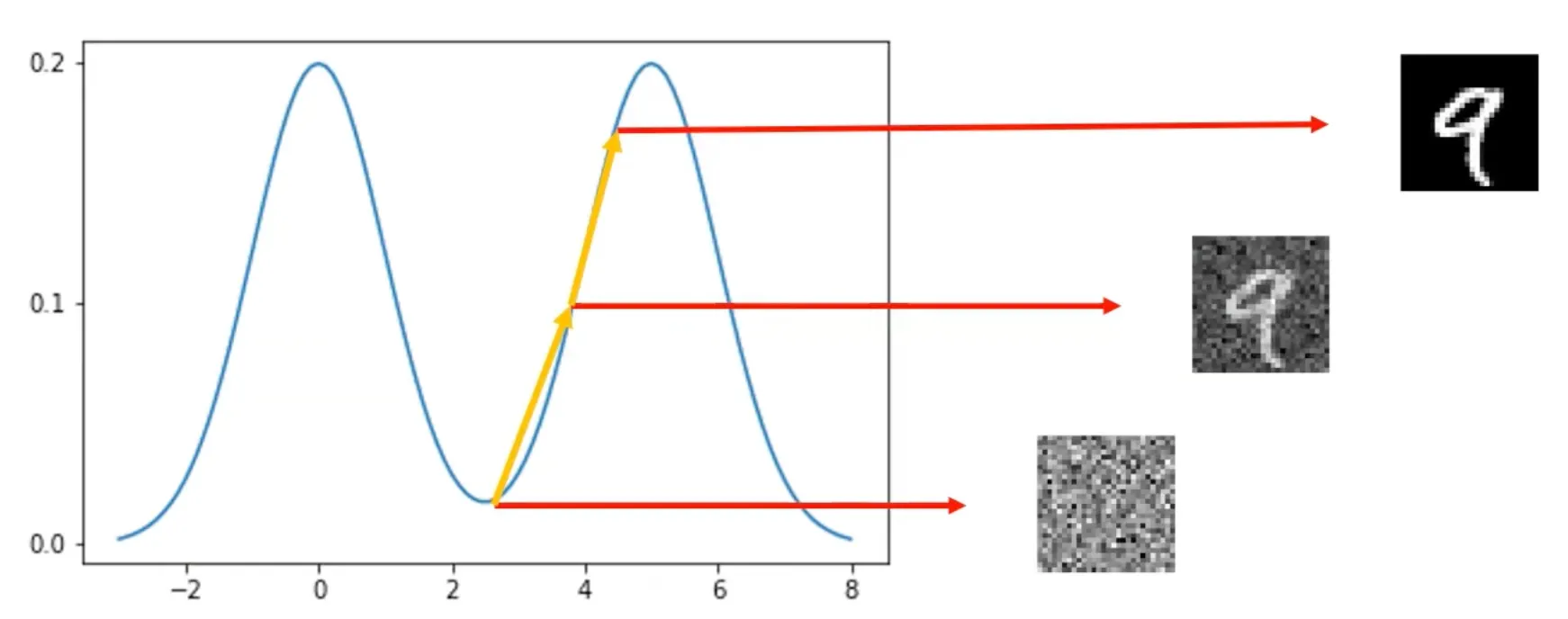
데이터 공간 상에서 임의의 데이터를 sampling → noise일 확률이 높음.

이를 Data의 probability density function p(x)p(x)p(x)의 gradient를 계산하여 probability가 높아지는 방향으로 데이터를 업데이트

여기서 이 기울기

\nabla_x \log p(x)

가 “score”에 해당한다.

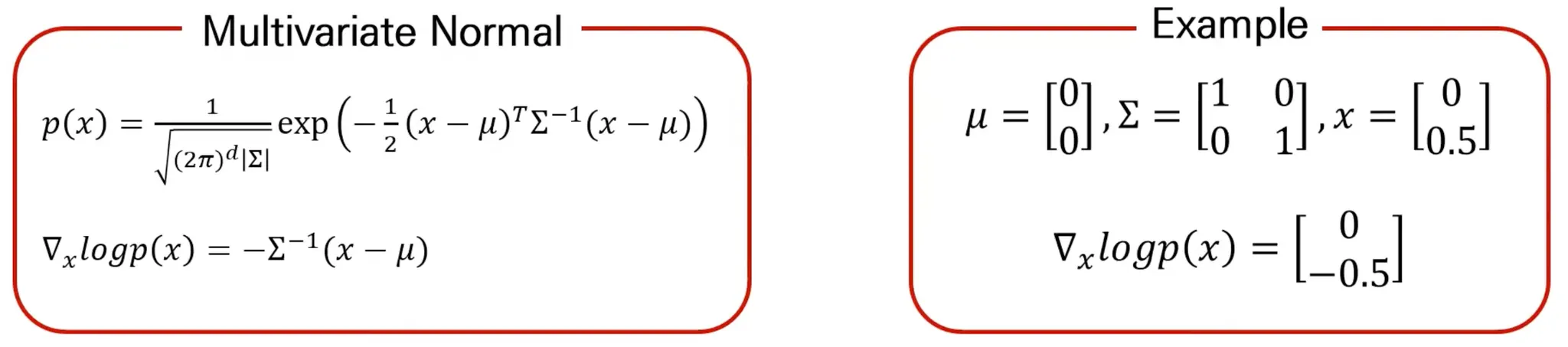
More about Score

즉, 입력 data와 score의 dimension이 동일함.

•

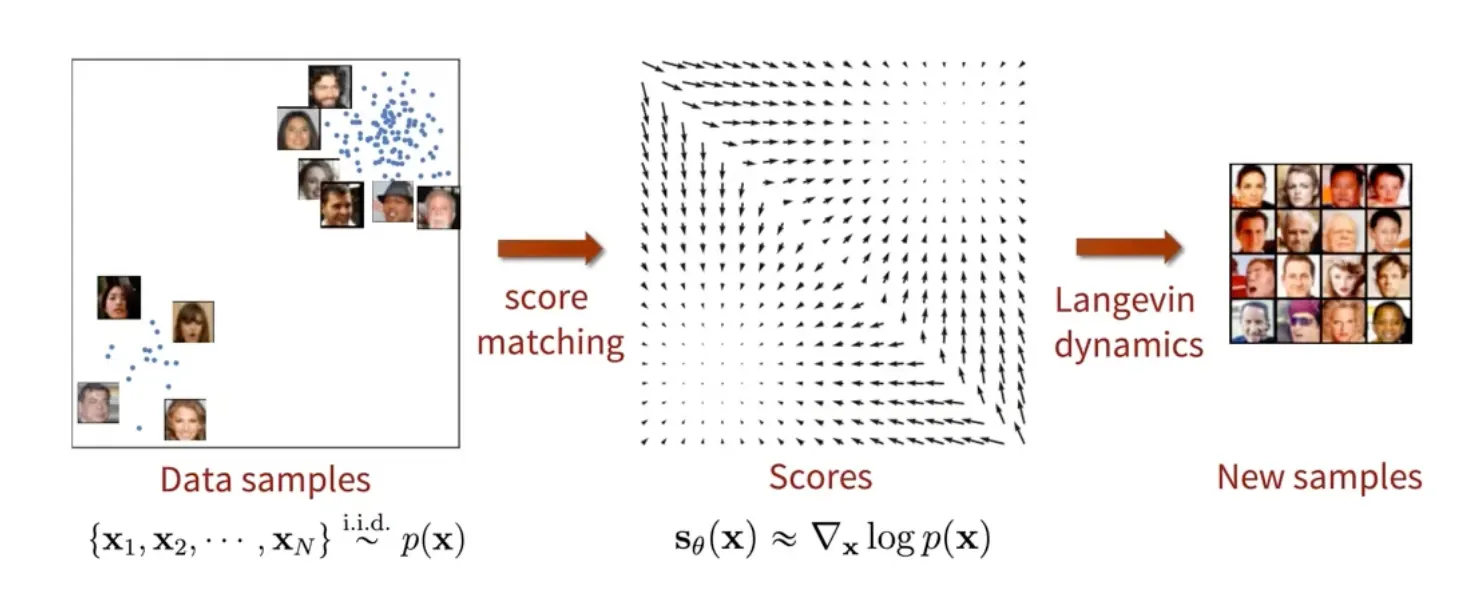
Data의 정확한 분포는 모르지만 score만 알면 data 생성 가능.

◦

Train 시에는 Score를 데이터로부터 추정 (Score matching)

◦

Test 시에는 추정된 score를 바탕으로 새로운 data를 sampling (Langevin dynamics)

•

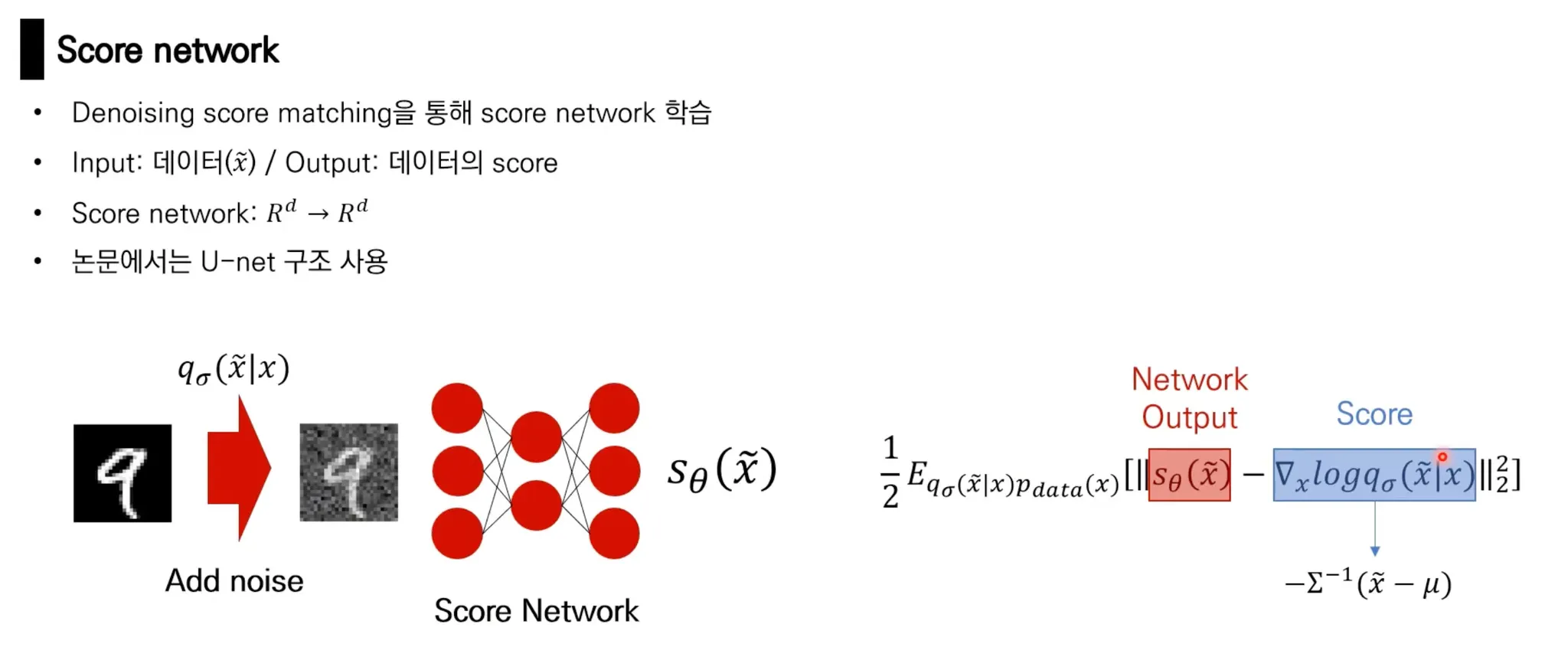
Score matching

Data

x

에 대해 score를 예측하는 model인 Score Network를 학습!

\mathcal{L} = \frac{1}{2}\mathbb{E}_{p_{\text{data}}(x)} \|\nabla_x \log p(x) - s_\theta(x)\|^2_2

그런데 ground truth score 자체가 intractable

방법 1.

s_\theta

의 Jacobian matrix를 사용해

p_{\text{data}}(x)

에 의존하지 않는 형태로 유도 (Hyvärinen, 2005)

\mathbb{E}_{p_{\text{data}}(x)} [tr(\nabla_x s_\theta(x)) + \frac{1}{2}\|s_\theta(x)\|^2_2]

실제 score를 추정할 수는 있지만, Jacobian을 구하는 것이 힘들어서 deep learning이나 high-dimension data에 확장하기 어려움.

방법 2. 원본 데이터에 대한 score를 계산하지 말고, 미리 정의된 noise distribution

q_\sigma(\tilde{x}|x)

를 이용해 perturbed data distribution에 대한 score matching (Vincent, 2011)

\frac{1}{2} \mathbb{E}_{q_\sigma (\tilde{x}|x)p_{\text{data}}(x)} [\|s_\theta(\tilde{x}) - \nabla_x \log q_\sigma (\tilde{x} | x)\|^2_2]

즉, data의 원본 distribution에 대한 density를 직접 계산하는 것은 intractable 하지만, 사전에 미리 정의한 perturbed data distribution에 대한 density는 계산가능하고, 이를 사용해 loss를 계산함.

s_{\theta *}(x) = \nabla_x \log q_\sigma(x) \approx \nabla_x \log p_{\text{data}}(x)

•

noise가 충분히 작으면 원래 data의 score와 비슷

•

Denoising score matching (Vincent, 2011)

dl.acm.org

https://dl.acm.org/doi/10.1162/NECO_a_00142

•

Langevin dynamics

◦

Score network가 잘 학습되었다면, 모든 data 공간 상에서 score 계산 가능.

◦

임의의 data (random noise)에서 시작하여 그 시점에서 추정된 score를 이용해 data를 update 한다.

◦

이를 반복하면 높은 probability를 가진 지역의 data를 생성할 수 있다.

\tilde{x}_t = \tilde{x}_{t-1} + \frac{\epsilon}{2} \nabla_x \log p(\tilde{x}_{t-1}) + \sqrt{\epsilon} z_t

•

Problem in Low Density Regions (Inaccurate score estimation)

◦

Data는 high probability 지역에서 sampling 됨.

◦

Low probability 지역에서의 score에 대한 정보가 별로 없으므로 부정확해진다. 

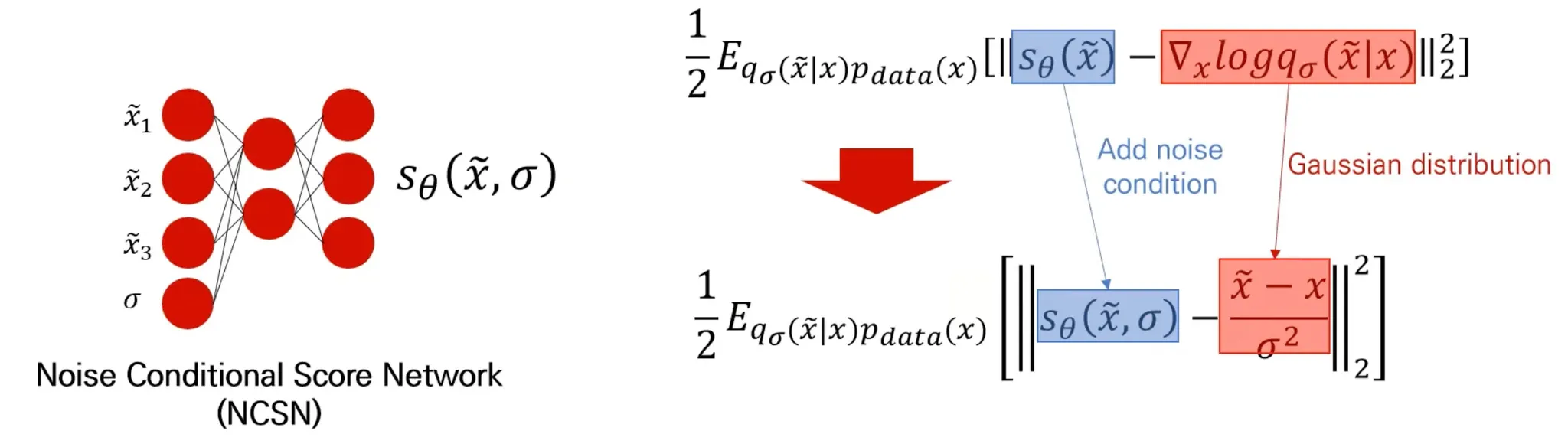
→ NCSN 제안

•

Noise Conditional Score Networks

Improved Techniques for Training Score-Based Generative Models

Score-based generative models can produce high quality image samples comparable to GANs, without requiring adversarial optimization. However, existing training procedures are limited to images of...

https://arxiv.org/abs/2006.09011

Data에 noise를 추가한 뒤에 score를 추정

◦

Input: Data (x~\tilde{x}x~) + Noise (σ\sigmaσ)

◦

Output: Score

◦

사전에 σ2\sigma^2σ2를 미리 정해서 사용함.

•

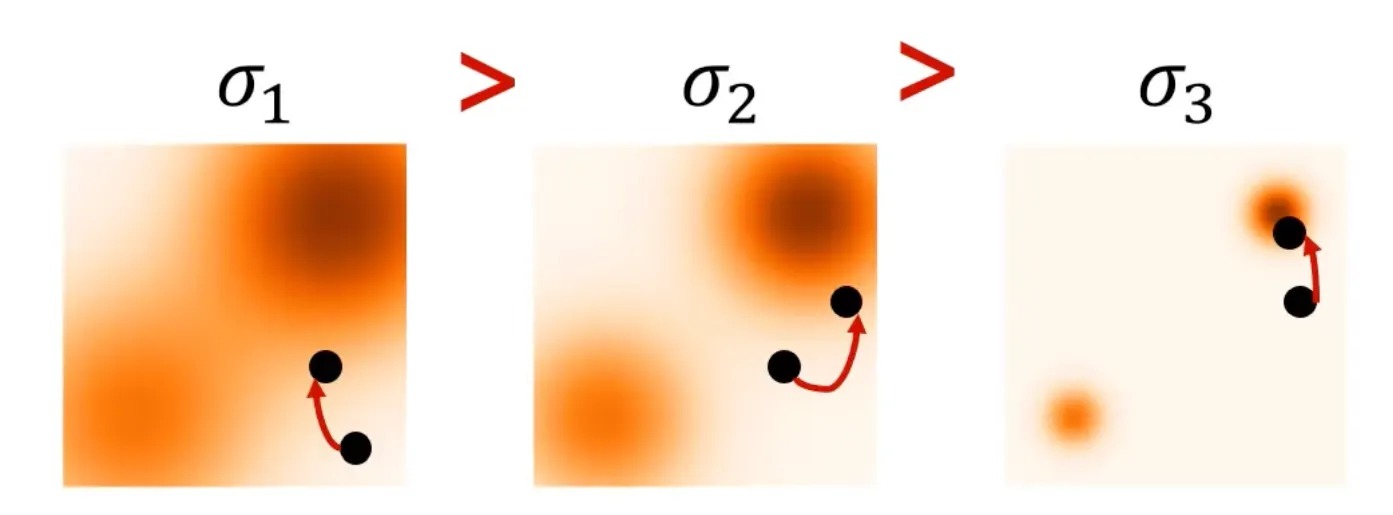
Annealed Langevin dynamics

◦

Noise schedule: Noise 크기를 감소시키며 sampling 진행

◦

Gradient ascent: T step만큼 data update

DDPM

•

MLE (Maximum Likelihood Estimation)

\text{Likelihood} = \prod p_{\mu, \sigma} (x)

모든 parameter에 대해 계산을 해볼 수 없으므로, 미분을 해서 각 parameter의 MLE를 알아내는 것이 일반적.

•

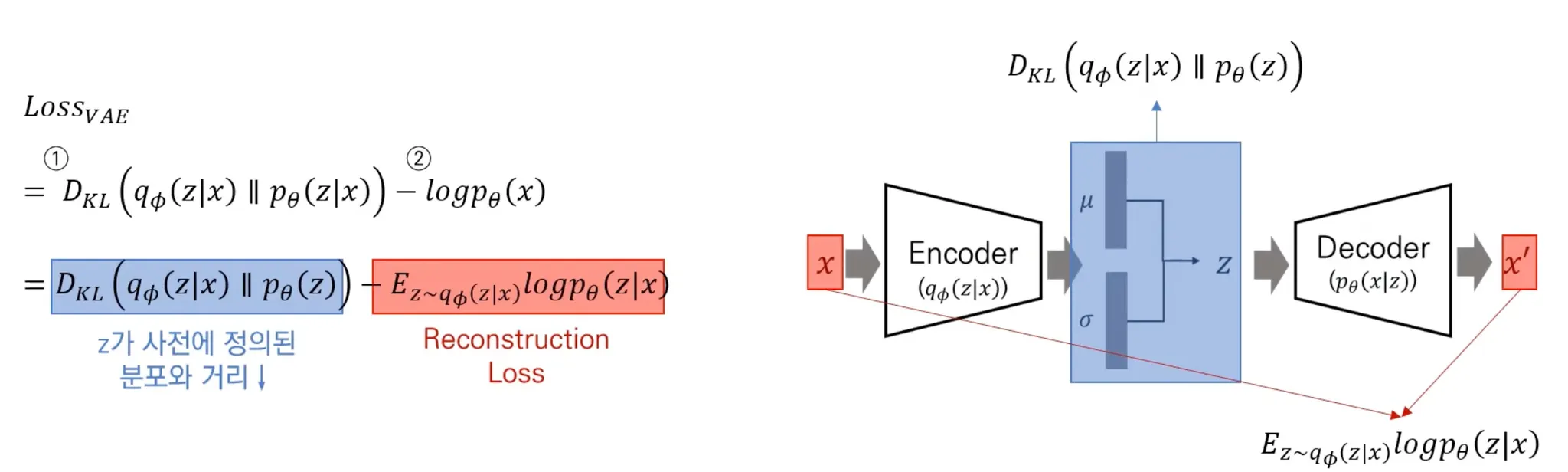
VAE (Variational AutoEncoder)

직접

p_\theta(x)

를 계산하기 어려우므로, Latent variable (

z

)로부터 data

x

를 생성

p_\theta (z|x)

: True distribution

q_\phi (z|x)

: Model (Encoder)

D_{KL}(q_\phi(z|x) \| p_\theta(z|x)) = \log p_\theta(x) + D_{KL} (q_\phi(z|x) \| p_\theta(z)) - \mathbb{E}_{z \sim q_\phi (z|x)} \log p_\theta(z|x)

◦

KL Divergence 최소화

◦

Likelihood 최대화

•

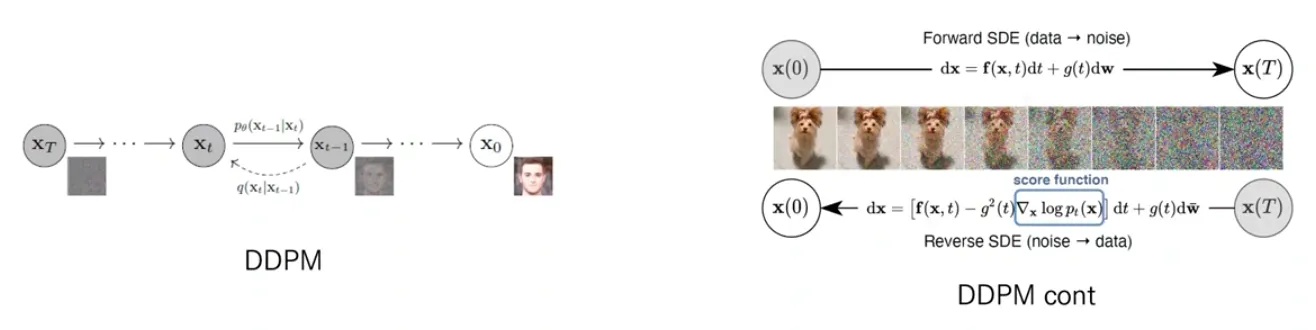
DDPM (Denoising Diffusion Probabilistic Models)

◦

Forward process: Add noise

Data (

x_0

) + Noise ⇒ Random noise (

x_T

)

◦

Reverse process: De-noise

Random noise (

x_T

) + Noise ⇒ Data (

x_0

)

◦

목적: reverse process를 학습

◦

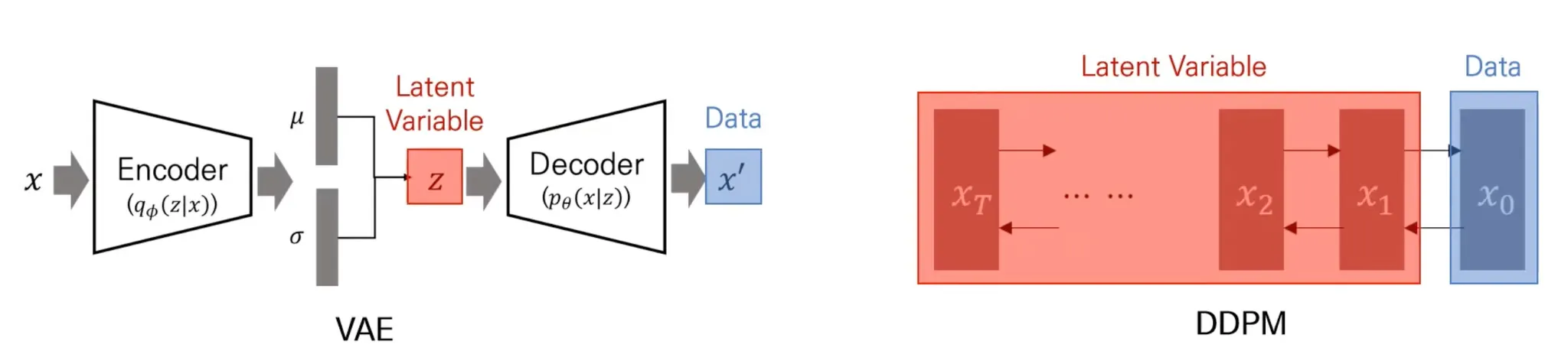
VAE vs DDPM

▪

둘 모두 latent variable model

▪

VAE는 latent variable 하나를 이용해서 data를 reconstruction.

▪

DDPM은 Markov chain 전체를 latent variable로 사용.

•

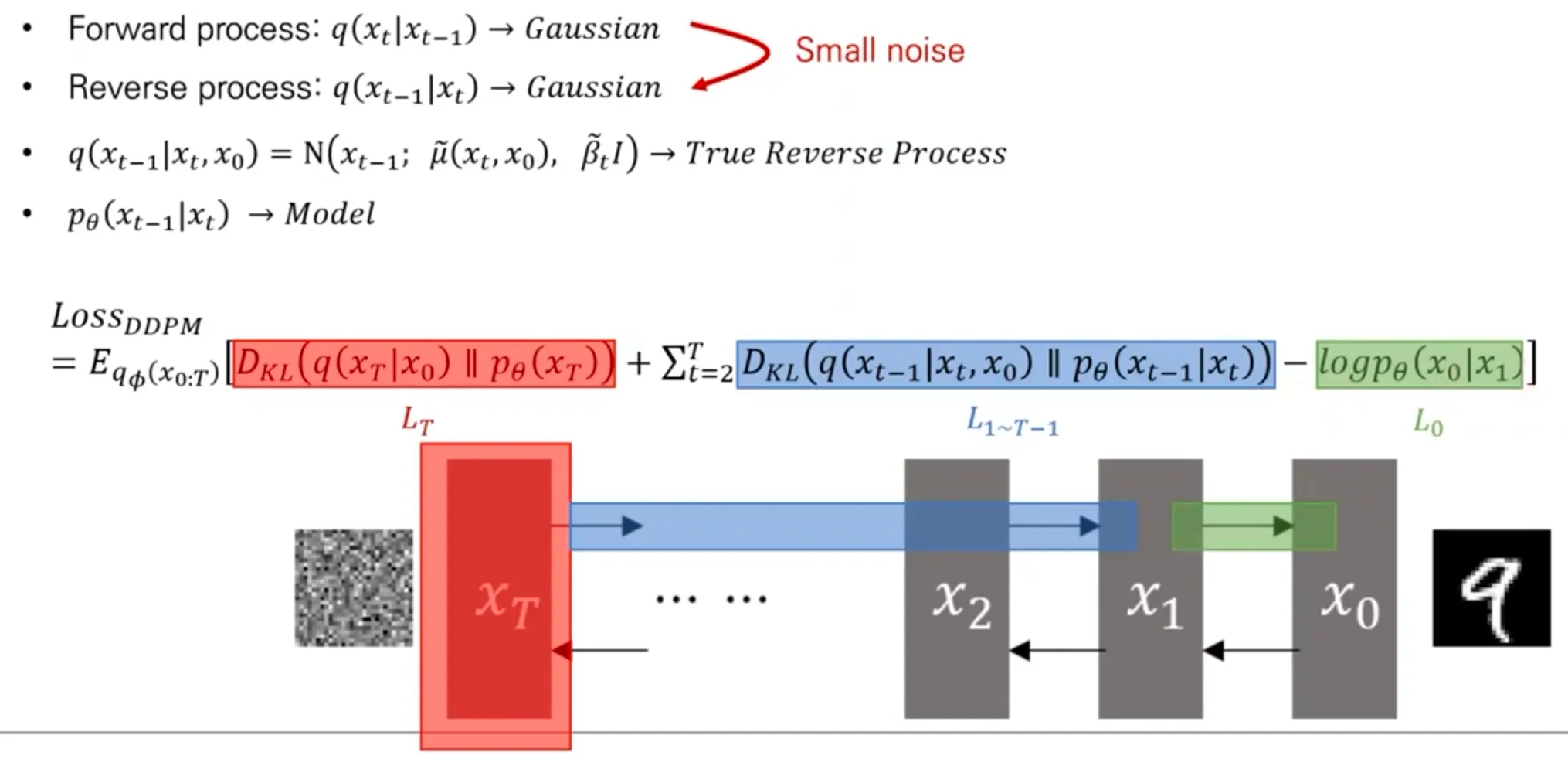
P(xn+1∣xn)=P(xn+1∣xn,xn−1,...,x0)P(x_{n+1} | x_n) = P(x_{n+1} | x_n, x_{n-1}, ..., x_0)P(xn+1​∣xn​)=P(xn+1​∣xn​,xn−1​,...,x0​)

◦

Loss

DDPM Loss 유도

◦

DDPM process

▪

Forward process가 “작은” Gaussian noise를 줬다면, reverse process도 Gaussian임이 증명되어 있다.

▪

실제 reverse process는 q(xt−1∣xt,x0)q(x_{t-1} | x_t, x_0)q(xt−1​∣xt​,x0​) 이고, model은 pθ(xt−1,xt)p_\theta (x_{t-1}, x_{t})pθ​(xt−1​,xt​)로 이 둘 간의 KL divergenge를 최소화하도록 학습된다.

▪

LTL_TLT​: 사전에 정의한 noise 분포랑 동일하도록 하는 loss term

▪

L1∼T−1L_{1 \sim T-1}L1∼T−1​: Reverse process를 model이 잘 학습하도록 하는 loss

▪

L0L_0L0​: 마지막으로 x0x_0x0​를 만들도록 하는 loss

▪

결국 model μθ(xt−1∣xt)\mu_\theta(x_{t-1}| x_t)μθ​(xt−1​∣xt​)이 추정하는 것은 Gaussian distribution의 평균 μ~(xt,x0)\tilde{\mu} (x_t, x_0)μ~​(xt​,x0​).

•

Variance는 Forward process의 βt\beta_tβt​로부터 유추되도록 설계되어 있음.

◦

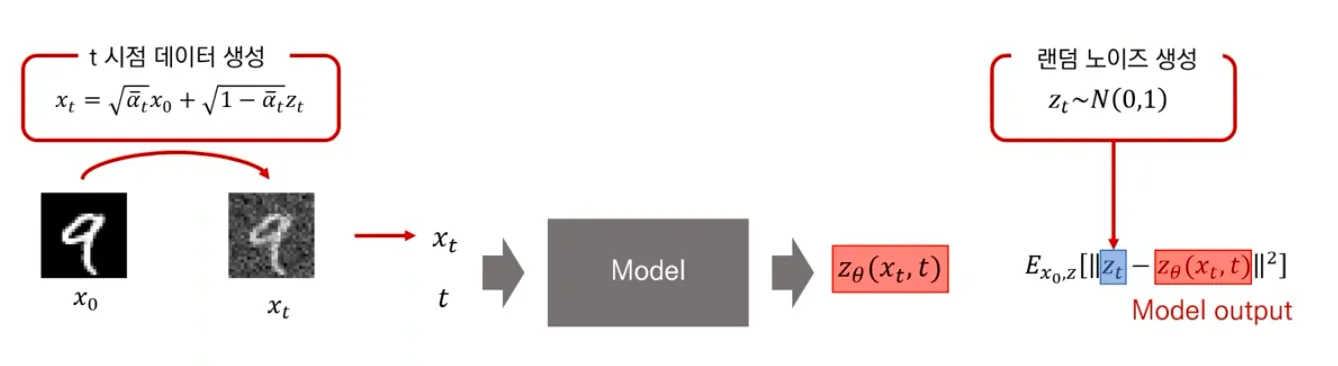
Training

▪

ttt 시점에서 diffused data xtx_txt​를 생성함 (noise를 time step ttt에 해당하는 만큼 더해줌)

▪

Diffused data xtx_txt​와 time step ttt를 model에 함께 넣어주고, model은 그 random noise를 prediction 하도록 학습된다.

◦

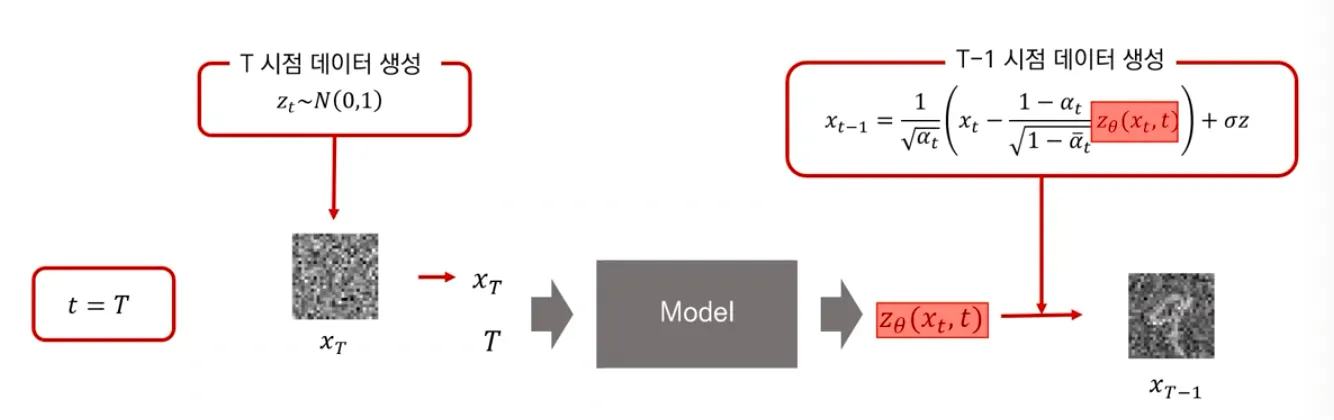
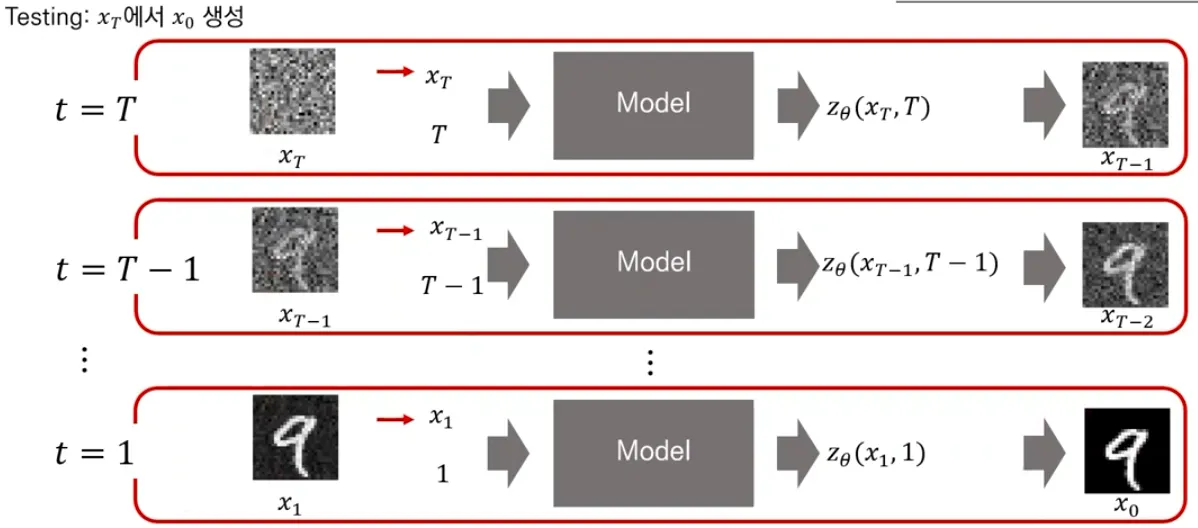
Testing

▪

xTx_TxT​ (noise) 에서 x0x_{0}x0​ 생성

▪

학습한 model을 사용해 얼만큼의 noise를 “denoise” 해주어야하는지 예측하고, 그만큼 더해서 점점 xtx_txt​에서 x0x_0x0​ 를 생성해냄.

◦

NCSN vs DDPM

▪

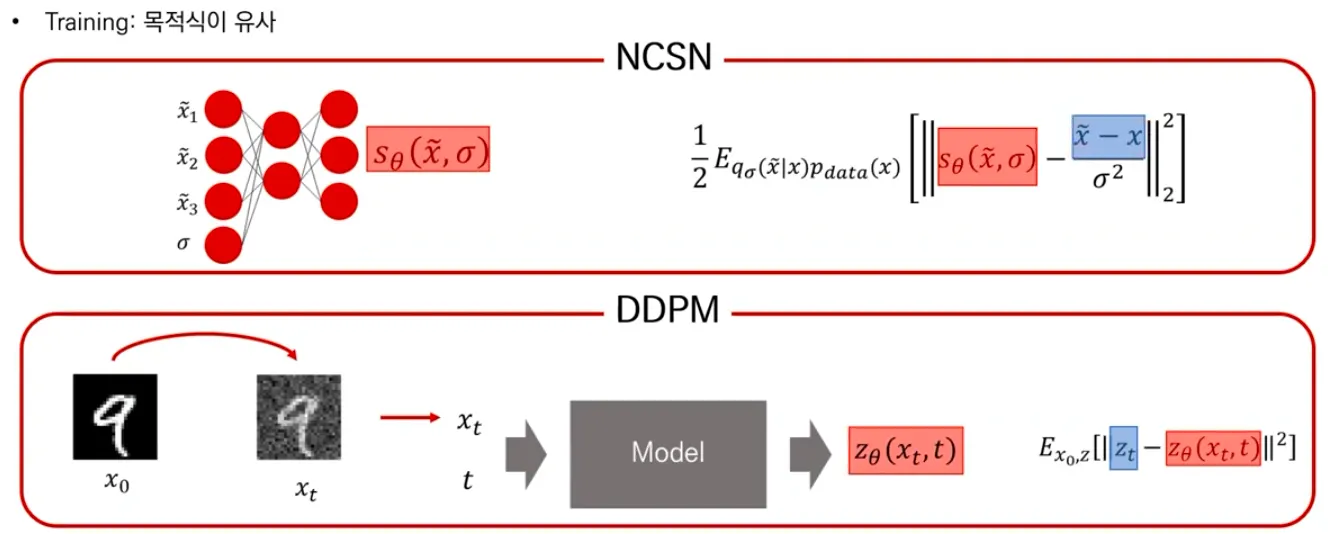
NCSN과 DDPM의 training은 objective function 자체가 비슷한 형식을 띄고 있음.

▪

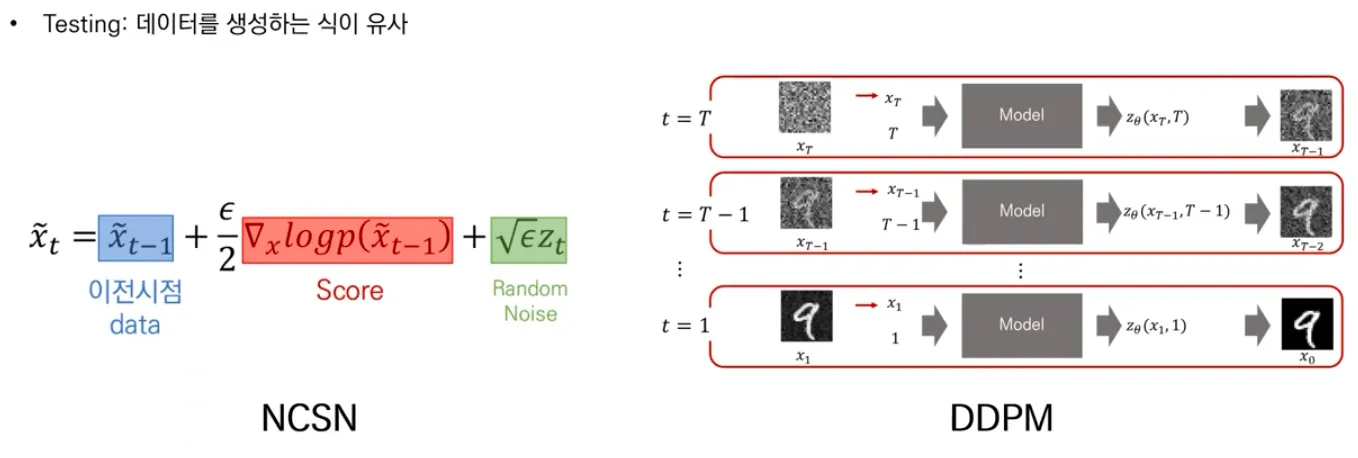
Testing 시에도 생성하는 식이 유사함. 이전 시점의 data (noisy data)에서 denoise를 해내는 과정.

DDIM: TODO

Score-based Generative Models Through SDEs

•

[Research article] Score-based Generative Models Through Stochastic Differential Equations (ICLR, 2021)

Score-Based Generative Modeling through Stochastic Differential Equations

Creating noise from data is easy; creating data from noise is generative modeling. We present a stochastic differential equation (SDE) that smoothly transforms a complex data distribution to a...

https://arxiv.org/abs/2011.13456

•

ODE (상미분방정식) and SDE

◦

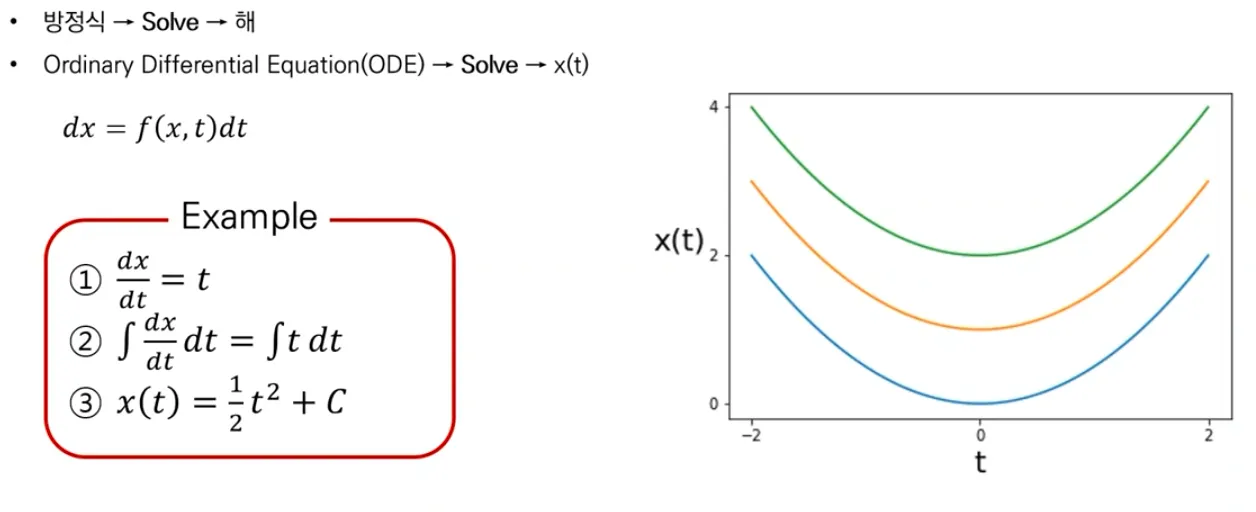
ODE

▪

ODE는 미분 방정식의 일종으로, 구하려는 함수가 하나의 독립 변수만을 가지고 있는 경우를 가리킨다.

◦

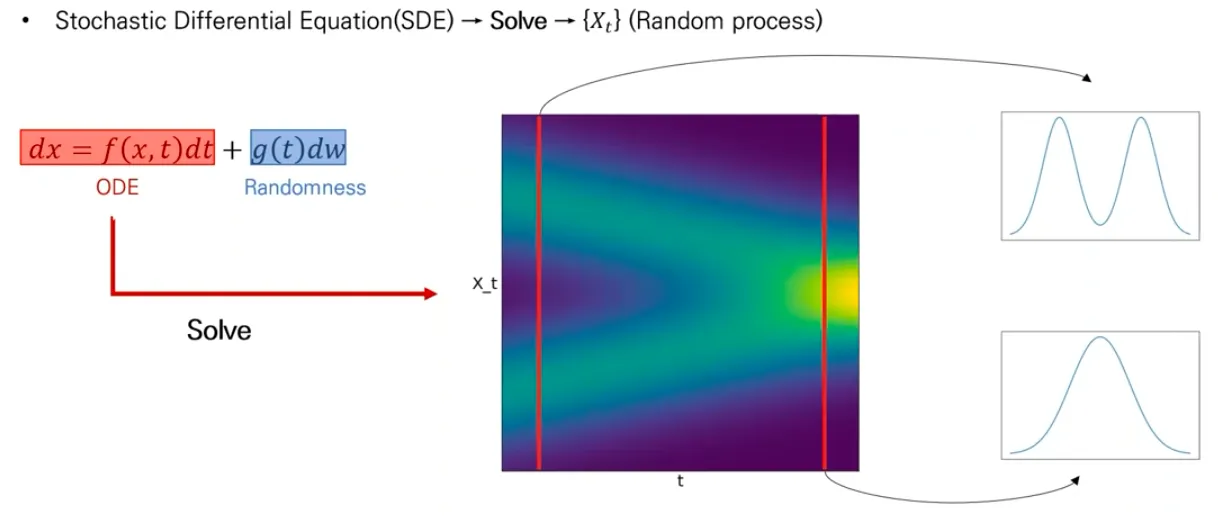
SDE: ODE + Randomness

▪

SDE는 1개 이상의 term이 stochastic 한 미분 방정식이다.

▪

General SDE는 아래 식으로 표현된다.

d\mathbf{x}_t = f(t)\mathbf{x}_t dt + g(t) d\omega_t

DDPM과 SDE의 연결

◦

SDE는 NCSN, DDPM의 continuous 버전이다.

▪

Forward SDE: noise를 추가하는 과정

Forward SDE of DDPM

•

Drift term이 ODE

•

Diffusion term이 stochastic term

▪

Reverse SDE: noise를 제거하는 과정

Reverse SDE of DDPM

•

1982년에 나온 논문에서 reverse SDE를 closed form으로 정리할 수 있다고 보임.

•

Score function을 어떻게 얻어야 하는가가 SDE의 핵심이다.

◦

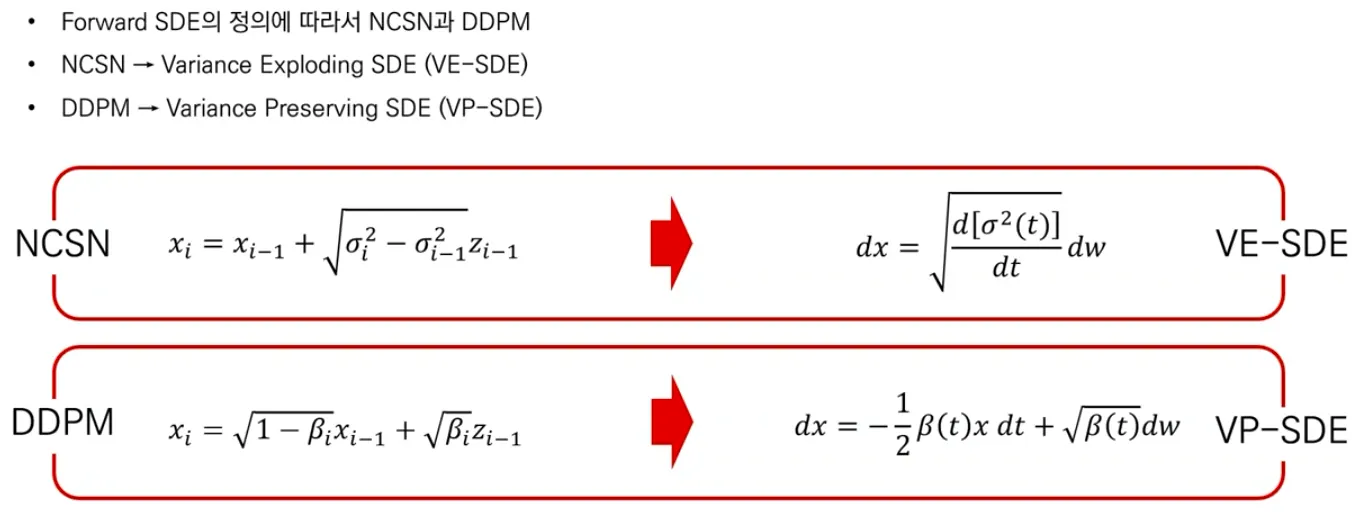
NCSM & DDPM

▪

Forward SDE를 어떻게 정의하느냐에 따라 NCSN, DDPM이 나뉜다.

▪

Time step에 따라 variance가 exploding 하는 NCSN은 VE-SDE, variance가 preserve 되는 DDPM은 VP-SDE.

◦

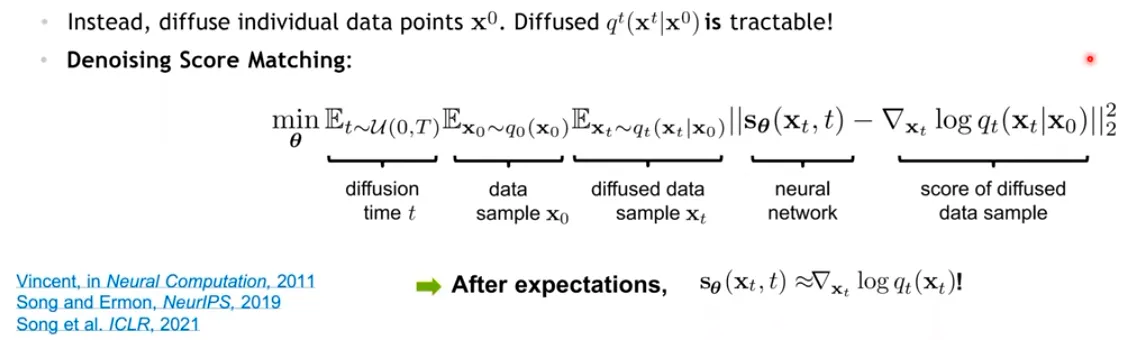
Training: Score network 학습 aka Score Matching

▪

Data 전체 분포에 대한 score를 계산하는 것은 intractable.

▪

따라서 score function을 추정하는 “score estimator”로써 neural network sθ(xt,t)\mathbf{s}_\theta(\mathbf{x}_t, t)sθ​(xt​,t)를 학습시키켜야 하고, 이를 “Score matching” 이라고 부른다.

▪

Naïve 하게는 direct regression으로 추정해볼 수 있지만, ∇xtlog⁡qt(xt)\nabla_{x_t} \log q_t(x_t)∇xt​​logqt​(xt​)가 intractable 하므로 목표를 알 수 없는 추정이라 풀 수가 없다.

▪

대신, 각각 data point x0\mathbf{x}^0x0에 대한 계산은 tractable 하다.

▪

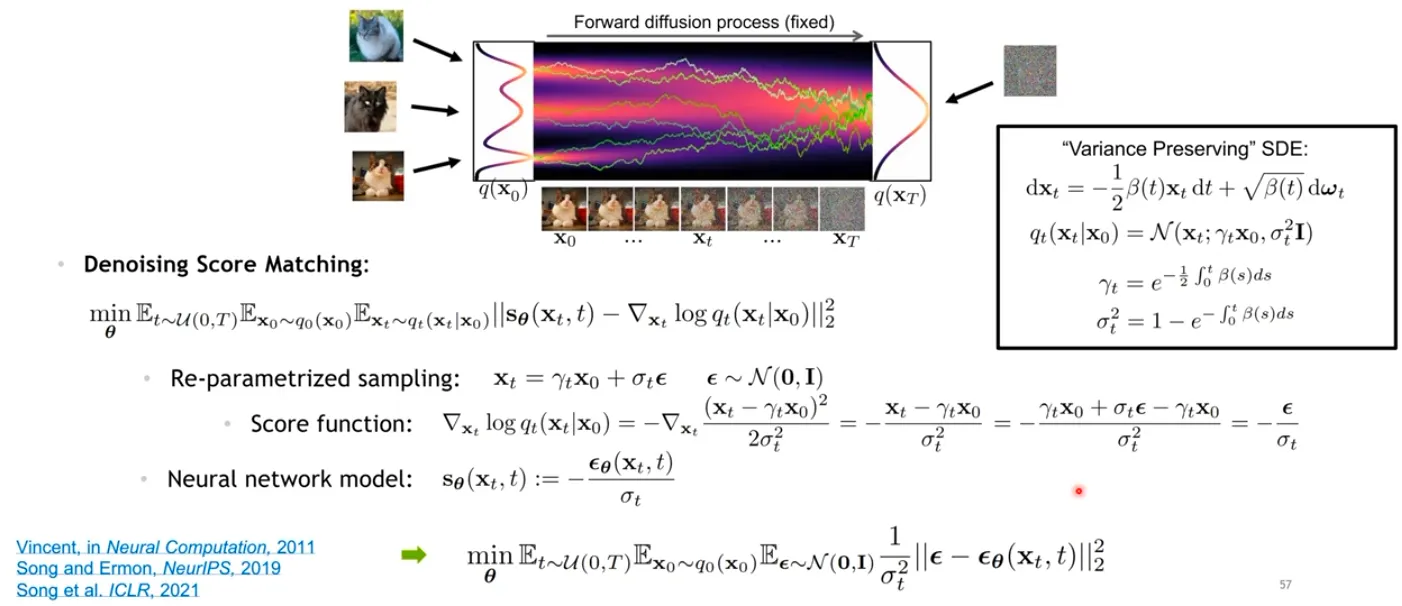
결국 이를 풀어보면, neural network는 time step ttt에서 가해진 noise를 예측하도록 학습이 된다.

▪

즉, DDPM과 NCSM은 SDE 식만 다른 것이고 결국 SDE 형태로 표현할 수 있는 개념인 것이다.

◦

Testing: Reverse SDE를 푸는 것

•

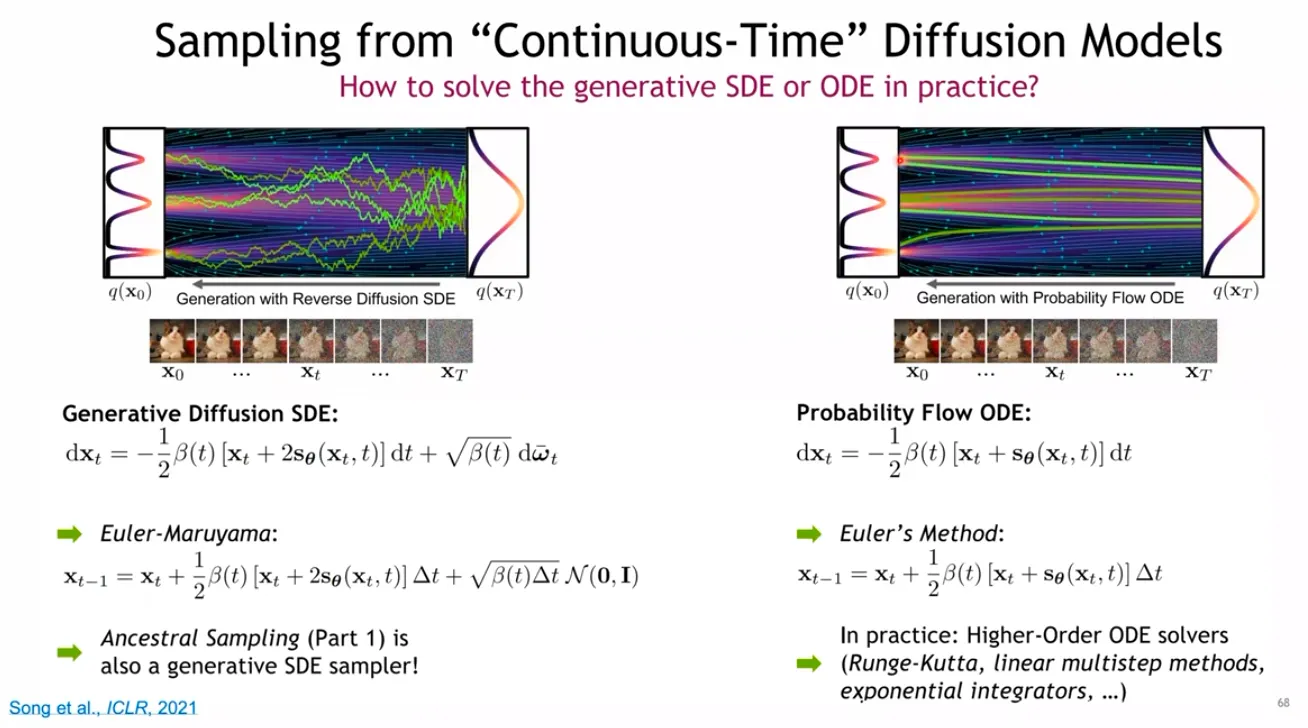
Probability Flow ODE

DDPM의 개념에서 randomness를 제거한 형태인 DDIM이 소개되었는데, SDE도 비슷하게 diffusion term을 제거한 ODE 형태로 randomness를 제거할 수 있다.

SDE의 경우 Gaussian noise가 계속 더해져서 이리저리 왔다갔다 하는 trajectory를 보이지만, ODE의 경우 직진성이 있는 trajectory를 보인다.

Conditional Diffusion Models: TODO

Classifier-guided

Classifier-free

Reference

Score-based Generative Modeling by Diffusion Process

Introduction to Score-based Generative Models Generative Model는 현실에 존재할만한 그럴듯한(High-fidelity) 이미지를 만들거나, Semi-supervised Learning, Few-Shot Learning 등의 문제에서 성능을 향상시키거나, 적대적 예제나 이상치 탐지를 하는 데 이용하는 등 다양한 응용 문제들에 활용될 수 있습니다. 대표적인 예로 흔히들 잘 알려져 있는 Autoencoder, VAE, GAN, Normalizing Flows를 들 수 있을 것입니다.

https://blog.si-analytics.ai/49

[Open DMQA Seminar] Score-Based Generative Models and Diffusion Models

https://youtu.be/d_x92vpIWFM

Generative Modeling by Estimating Gradients of the Data Distribution

This blog post focuses on a promising new direction for generative modeling. We can learn score functions (gradients of log probability density functions) on a large number of noise-perturbed data distributions, then generate samples with Langevin-type sampling.

https://yang-song.net/blog/2021/score/

Tutorial

The Annotated Diffusion Model

We’re on a journey to advance and democratize artificial intelligence through open source and open science.

https://huggingface.co/blog/annotated-diffusion

Introduction to Diffusion Models for Machine Learning

The meteoric rise of Diffusion Models is one of the biggest developments in Machine Learning in the past several years. Learn everything you need to know about Diffusion Models in this easy-to-follow guide.

https://www.assemblyai.com/blog/diffusion-models-for-machine-learning-introduction/