Search

Dihedral angle (이면각) 계산하기 - Python

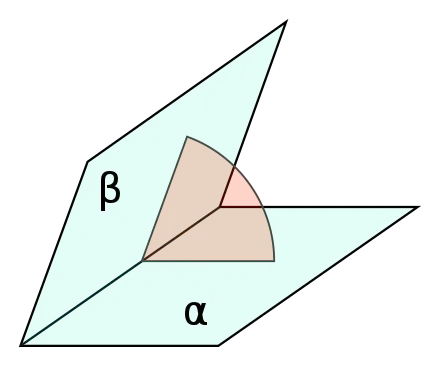
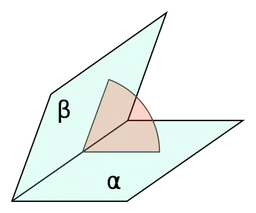
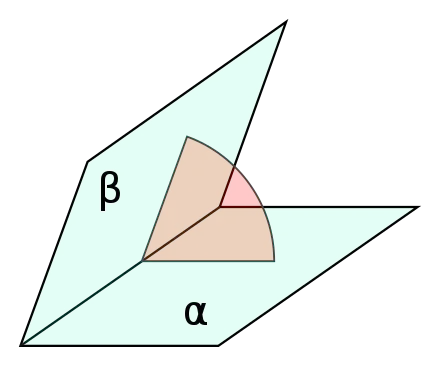
Dihedral angle (이면각)

Dihedral angle (이면각)이란 두 평면이 이루는 각도를 의미한다.
화학이나 단백질 구조를 다룰 때 많이 등장하는 개념이다.

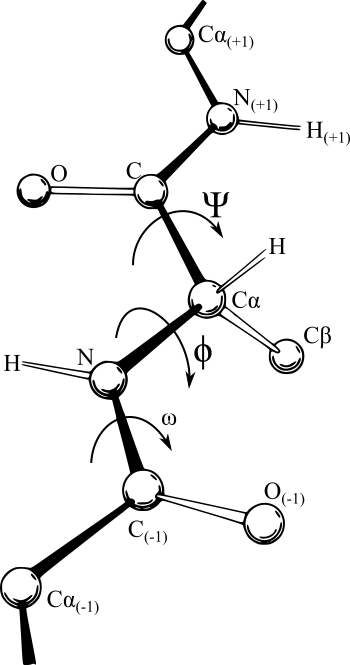
Dihedral angle in protein structure

펩타이드 형태로 연결된 각 아미노산마다 총 세 가지의 dihedral angle을 정의할 수 있다.
•
ω:Cprevα−C′−N−Ccurrα\omega: C^\alpha_{\text{prev}} - C'-N-C^\alpha_{\text{curr}}
•
ϕ:Cprev′−N−Cα−Ccurr′\phi: C'_{\text{prev}}-N-C^\alpha - C'_{\text{curr}}
•
ψ:Nprev−Cα−C′−Ncurr\psi: N_{\text{prev}}-C^\alpha-C'-N_{\text{curr}}
즉, 각 dihedral angle은 네 개의 atom으로 정의할 수 있으며, 네 개의 atom 중 [앞 세 개의 atom이 이루는 평면]과 [뒤 세 개의 atom이 이루는 평면]이 이루는 각도이다.
아미노산의 dihedral angle을 이야기할 때, 각 angle의 범위는 (−π,π)(-\pi, \pi)이다.
참고) Ramachandran plot

Graphical understanding of dihedral angles

그림을 사용하면 좀 더 쉽게 이해할 수 있다.
위 노트를 해설해보자면,
1.
먼저, 이면각의 부호가 +, - 인 경우를 생각해보자.
그림 (A), (B)
한 평면을 고정하고 다른 평면의 각도를 쟀을 때, π(=180°)\pi (=180 \degree)를 안 넘어가면 그 각도는 양의 부호를 가진다.
그림 (C)
반면, π(=180°)\pi (=180\degree)를 넘어가면, 그 각도는 음의 부호를 가진다. 이것을 꼭 기억하자!
2.
따라서 우리가 구하고자 하는 것은 이면각의 ‘절대값’과 ‘부호’이다.
3.
먼저, 이면각의 절대값은 두 평면의 법선 벡터 n1n_1과 n2n_2를 알면 구할 수 있다.
점 세 개가 일직선 상에 있지 않다면, 하나의 평면을 이룬다.
따라서 각 평면의 법선 벡터는 점 세 개가 서로 이루는 두 벡터를 외적해서 구할 수 있다.
n1=b0×b1,n2=b1×b2n_1 = b_0 \times b_1, n_2 = b_1 \times b_2
두 법선 벡터가 이루는 각도가 두 평면이 이루는 각도와 같다.
cos⁡(θ)=n1⋅n2∣n1∣∣n2∣∣θ∣=arccos⁡(n1⋅n2∣n1∣∣n2∣)\cos(\theta) = \frac{n_1 \cdot n_2}{|n_1||n_2|} \\ |\theta| = \arccos \Big(\frac{n_1 \cdot n_2}{|n_1||n_2|}\Big)
이때 arccos⁡\arccos (또는 다른 말로 cos⁡−1\cos^{-1})의 치역은 (0,π)(0,\pi)이기 때문에, 항상 양의 부호만 얻을 수 있다.
참고) arccos⁡\arccos 함수 그래프
즉, arccos⁡\arccos 만으로는 절대값만 알 수 있고, 부호는 제대로 알 수가 없다.
4.
이면각의 부호는 n1n_1과 n2n_2의 외적 벡터 (수직 방향)와 두 평면에 존재하는 임의의 벡터가 이루는 각도를 계산하면 알 수 있다.
위 그림에서는 예시로 k=n1×n2k = n_1 \times n_2와 b1b_1이 이루는 각도 θ′\theta'를 기준으로, θ′\theta'가 (0,π2)(0,\frac{\pi}{2})에 있으면 +, θ′\theta'가 (π2,π)(\frac{\pi}{2}, \pi)에 있으면 - 임을 알 수 있다.
이는 곧 cos⁡(θ′)\cos(\theta')의 부호, 또는 kk와 b1b_1의 dot product의 부호와 일치한다.
참고) cos⁡\cos 함수 그래프
5.
최종적으로 우리가 구하고자 하는 이면각 θ\theta는 아래의 식으로 구할 수 있다.
θ=sign(dot(k,b1))∗arccos⁡(n1⋅n2∣n1∣∣n2∣)\theta = \text{sign}(\text{dot}(k, b_1)) * \arccos \Big(\frac{n_1 \cdot n_2}{|n_1||n_2|}\Big)