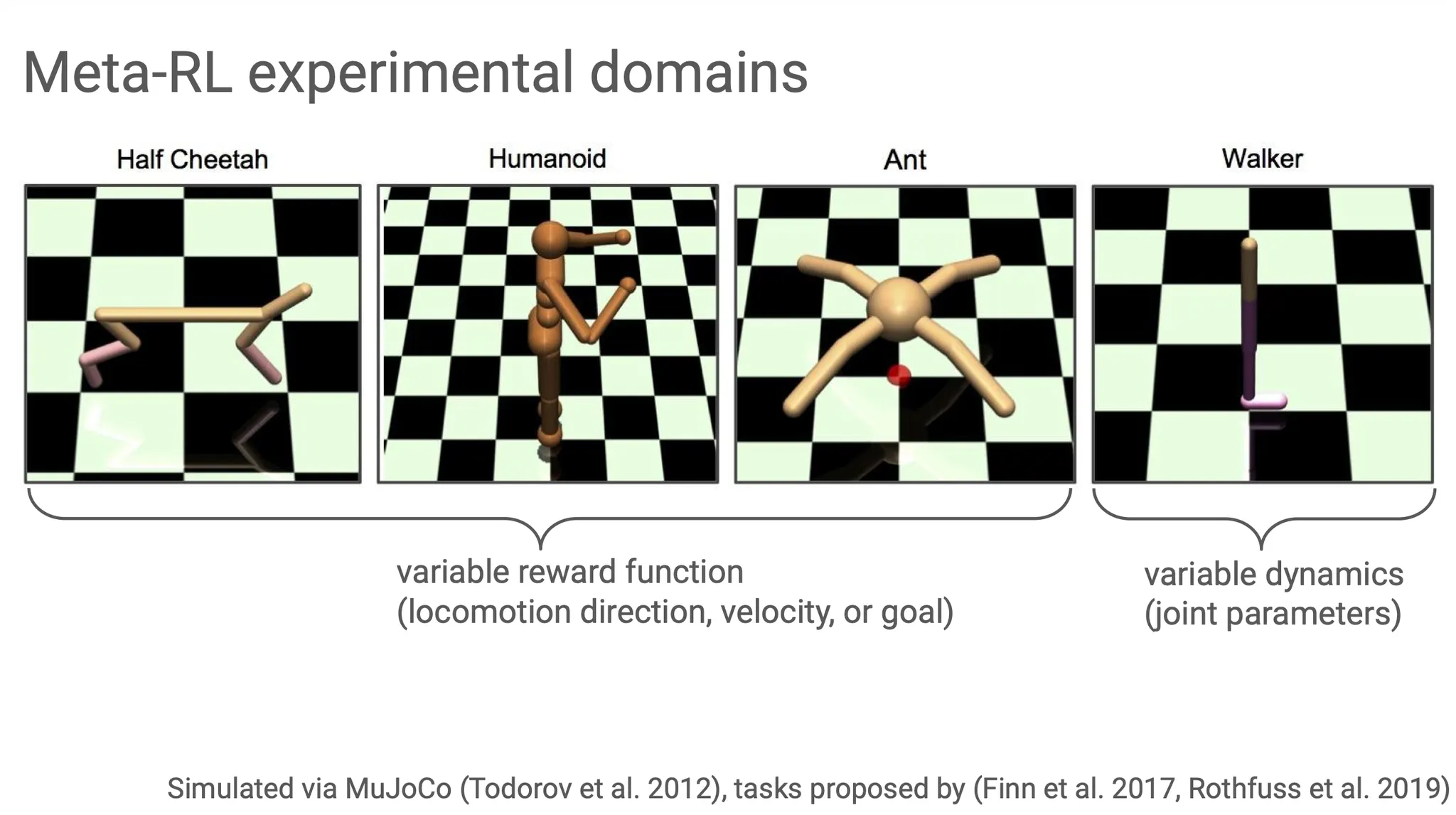
많은 연구들이 RL 상황에서 특정 task를 잘 수행하는 specialist가 되도록 학습을 유도하지만, real-world에서는 generalist agent가 필요하다. 다양한 task에 잘 적응해 빠르게 학습할 수 있도록 강화학습을 진행하는 것이 meta-RL이라고 할 수 있다.
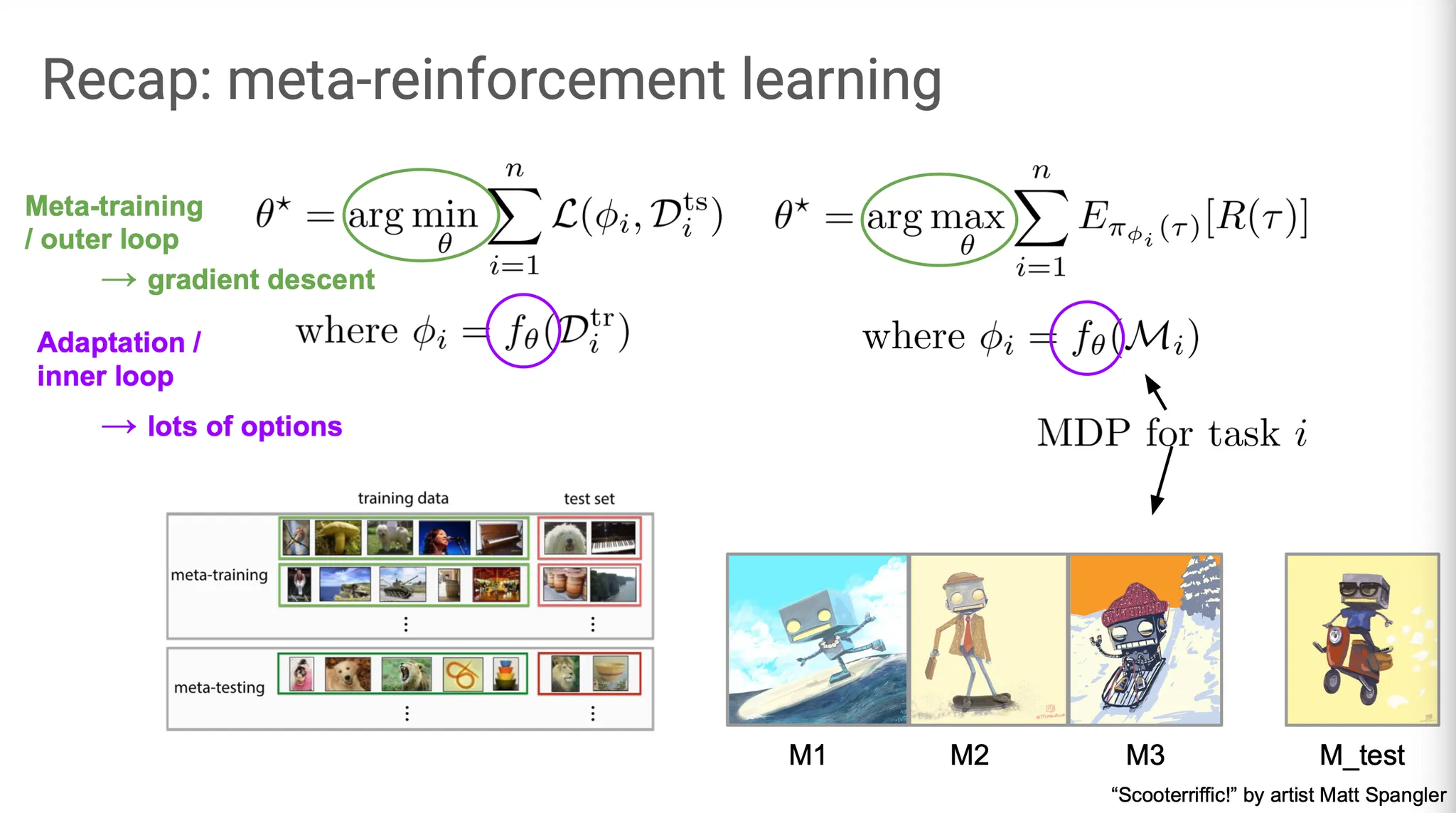
Meta-supervised learning(SL)의 경우에는 몇 개의 training data만을 보고도 test data를 맞출 수 있도록 학습이 진행된다. 각 task(여기서는 한 줄의 row)에 맞는 model parameter 를 학습하고, 그 과정에서 얻은 정보를 바탕으로 meta-parameter 를 update한다.
Meta-RL에서는 MDP(Markov decision process)에 adapt하도록 학습된다. 여러 MDP set에 대해 학습하여 general knowledge를 축적한다. 이번 강의에서는 를 adaptation(inner loop)이라고 부르고, 를 meta-training(outer loop)이라고 부른다. Outer loop은 대부분 gradient descent(적어도 optimization 기반의 방법들은)로 update되지만 inner loop은 다양한 선택지가 있고, 이번 강의에서 이들을 살펴본다.
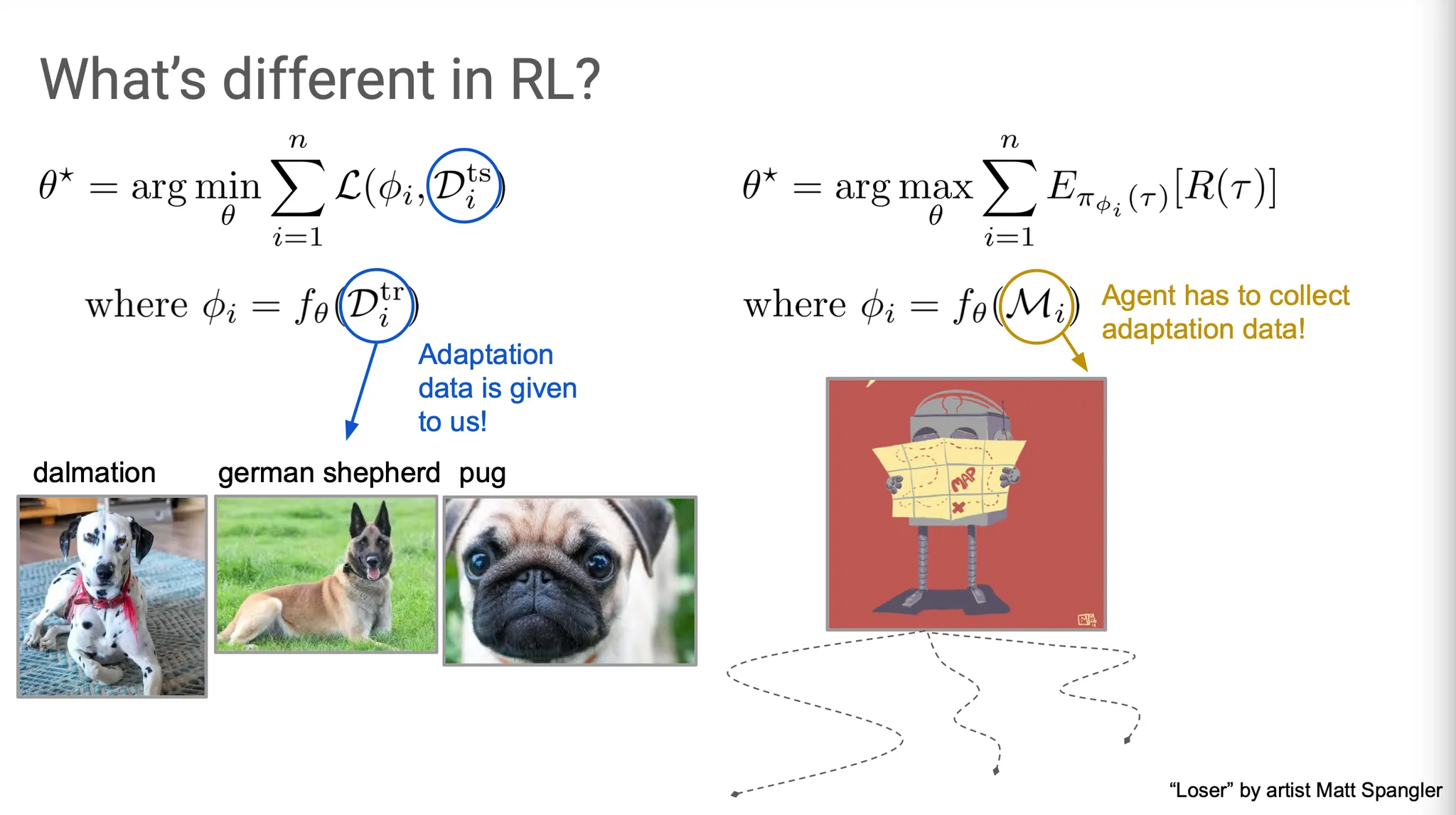
SL과 RL의 결정적인 차이는 무엇일까?
주된 차이는 model 학습 방법보다도 data가 어떻게 구성되어 있는지에 있다. SL에서는 data가 우리에게 그냥 주어지고, RL에서는 agent가 data를 수집한다. 즉, meta-RL에서는 data에 adapt해야할 뿐만 아니라, adapt 하기 위해 적합한 data를 수집하는 방법도 학습해야 한다.
Policy gradient 방식의 meta-RL algorithm은 먼저 현재 policy 에 따라 MDP data를 sampling하고, 그에 맞는 reward를 반영한 objective function을 계산한 뒤, policy gradient로 를 update한다. 이는 trial and error 개념을 formalize 한 것으로, 좋은 것(high reward)은 더 많이, 안 좋은 것(low reward)은 더 적게 학습하도록 하는 방법이다.
Policy gradient를 meta-learning algorithm으로 사용하는 방법은 어떤 것들이 있을까?
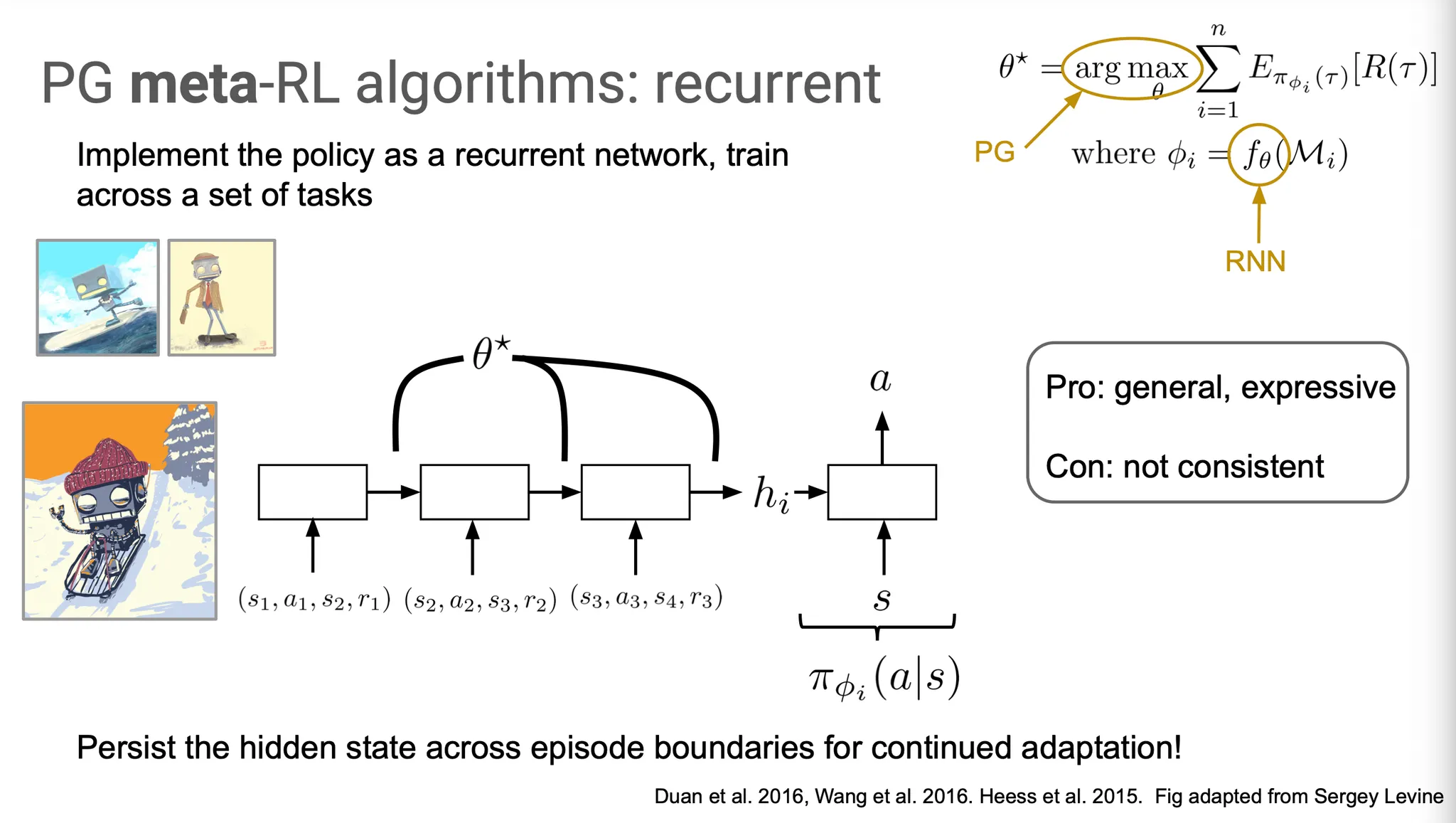
한 가지 option은 RNN을 사용하는 것이다. Task들을 학습하면서 얻은 information을 기억하는데 RNN cell의 hidden state를 사용할 수 있다. 즉, adaptation을 위한 를 RNN으로 설정할 수 있다.
이 방법의 장점은 general 하게 적용할 수 있고, RNN의 개념을 그대로 사용할 수 있어서 expressive 하다는 점이다. 하지만 단점으로는 RNN이 converge 하기는 할지, 그리고 어떤 상태로 converge할지를 guide할 수 없고 단지 뭔가 그럴듯한 정보들을 잘 학습할 것으로 기대할 수 밖에 없다는 점에서 consistent 하지 않다는 점을 들 수 있다.
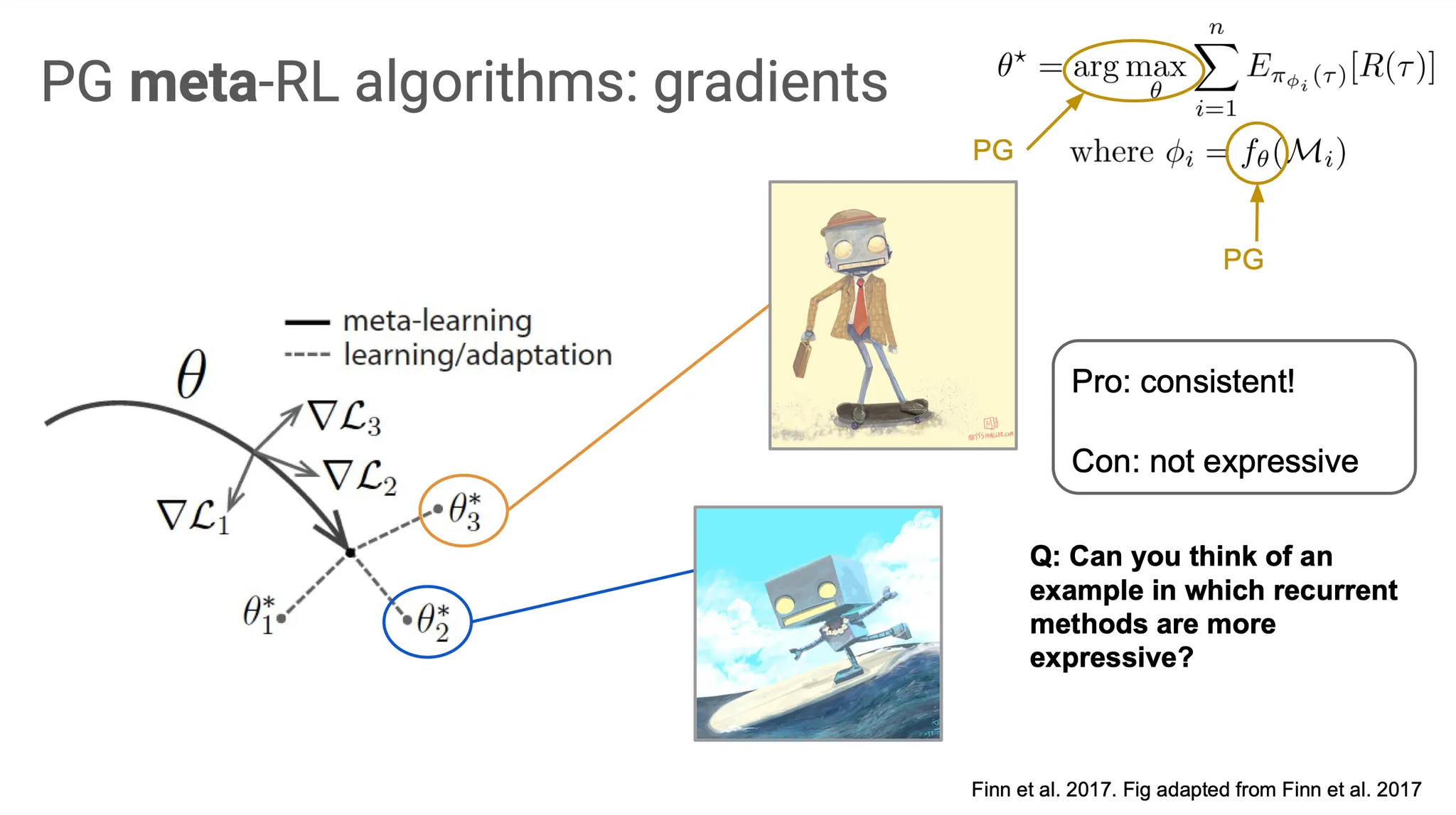
다른 방법을 생각해보자. 를 update할 때처럼, 를 update할 때도 policy gradient를 사용하면 어떨까? 사실 MAML이 이 방법을 사용하고 있다. Task-specific parameter 를 update할 때 gradient를 사용한다. 이 방법은 gradient descent를 사용하기 때문에 적어도 local minima로 converge 할 것이고, 주어진 MDP에서 optimal한 들을 학습할 수 있다는 점에서 consistent하다고 할 수 있다. 하지만 RNN model만큼 expressive 하지는 않다는 점이 단점이다.
여기서 RNN이 더 expressive 한 경우는 어떤 것이 있을지 생각해보자. 만약 최종 reward가 0 인 경우에 gradient 방식은 어떤 문제가 있을까? Gradient가 전혀 update 되지 않을 것이다. 새로운 환경의 dynamics를 분명히 봤음에도 불구하고, 이를 전혀 반영하지 못 하는 것이다. RNN의 경우에는 비록 어떤 보장은 못 하더라도, reward가 0인 episode에서도 새로운 환경에서 얻은 경험을 축적했을 것이라고 기대할 수 있다.
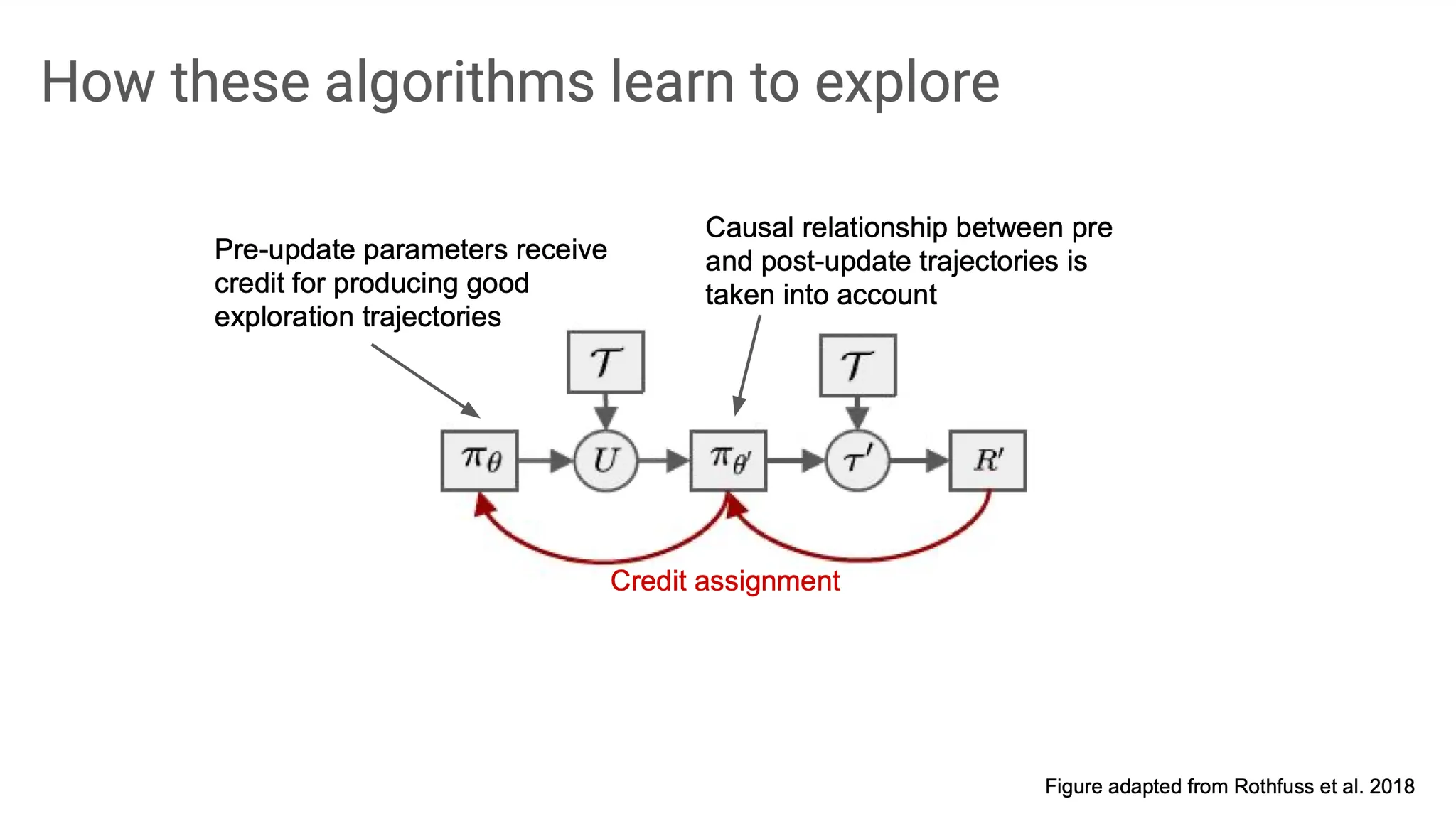
흐름을 다시 정리하자면, initial policy 에서 exploration trajectory 를 sampling 하고, 이를 바탕으로 update()하여 업데이트된 policy 를 얻는다. 여기서 다시 새로운 exploration trajectory 을 얻고, reward를 계산한다. 이후 gradient descent로 과 각각에 gradient를 전파한다. 이 단계를 credit assignment라고 부르기도 한다.
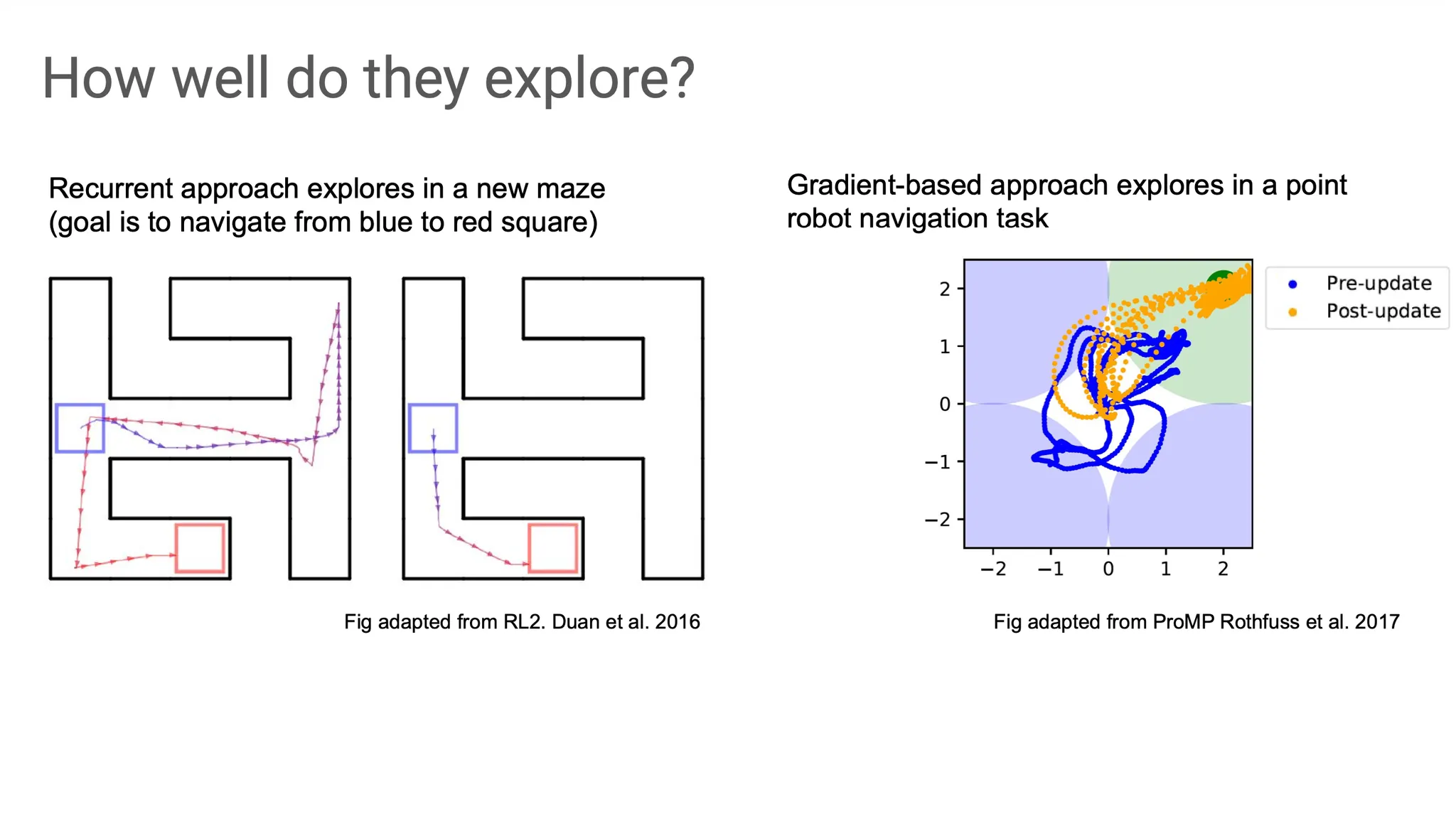
실제 task에서 작동하는 방식의 예시이다. 기본적으로는 exploration을 하게 되고, 그 과정에서 얻게 되는 reward 쪽으로 update되어 좀 더 나은 policy를 학습하게 된다. 이런 상황은 reward가 초기에는 sparse해서 exploration을 할 수 밖에 없게 된다.
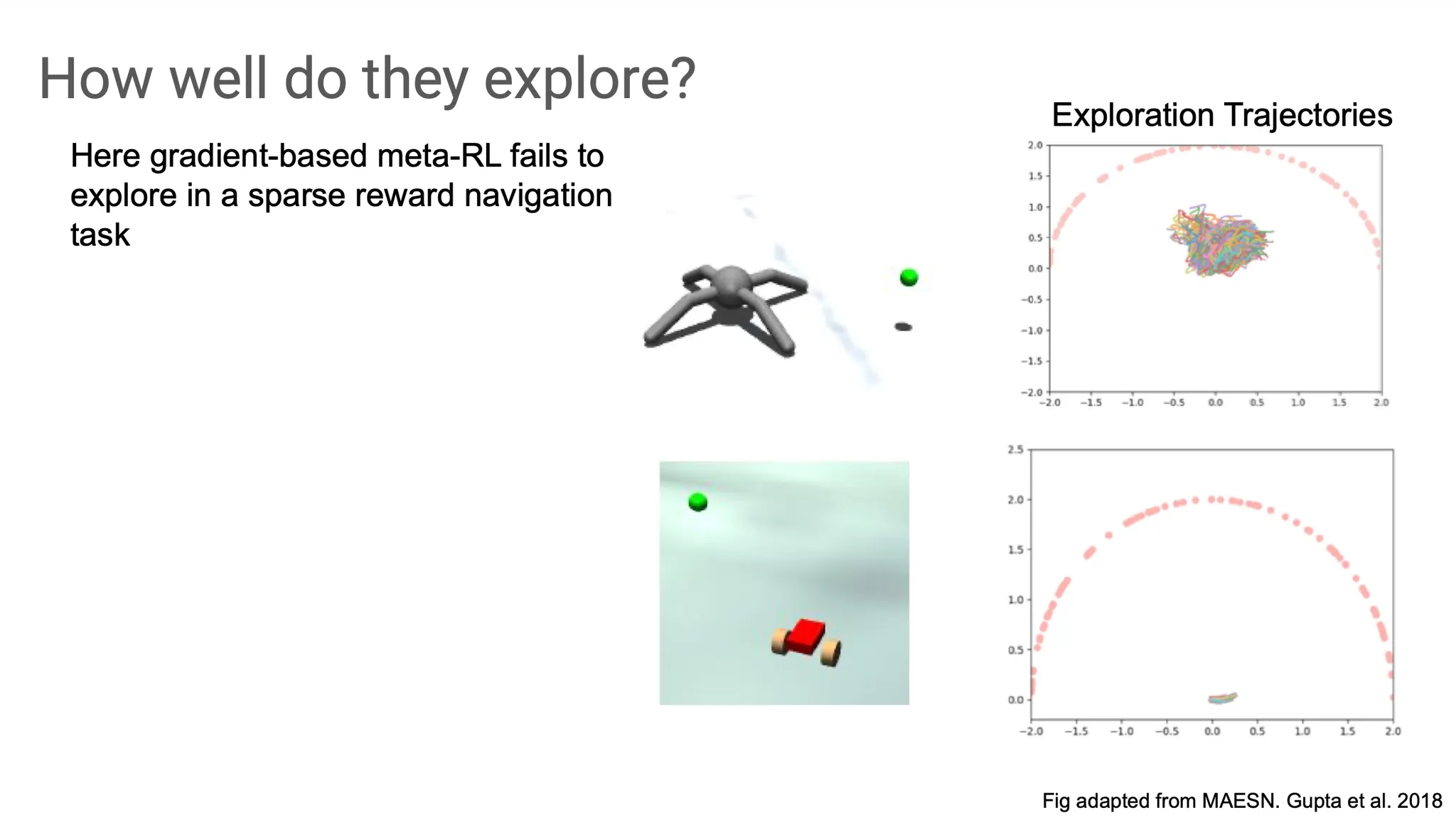
하지만 학습이 잘 안 되는 경우도 존재한다. Goal이 너무 멀리 있어서 reward가 sparse 한 상황에서 근처에만 맴돌다가 결국 goal state에 전혀 도달하지 못하는 경우가 생긴다.
무엇이 문제일까? 그것은 의미없는 탐색이 반복되면서 coherent하지 않게 되기 때문이다. 특히 reward가 sparse하고 goal state가 initial state로부터 멀리 떨어져 있을수록 학습이 잘 안 될 가능성이 높다.
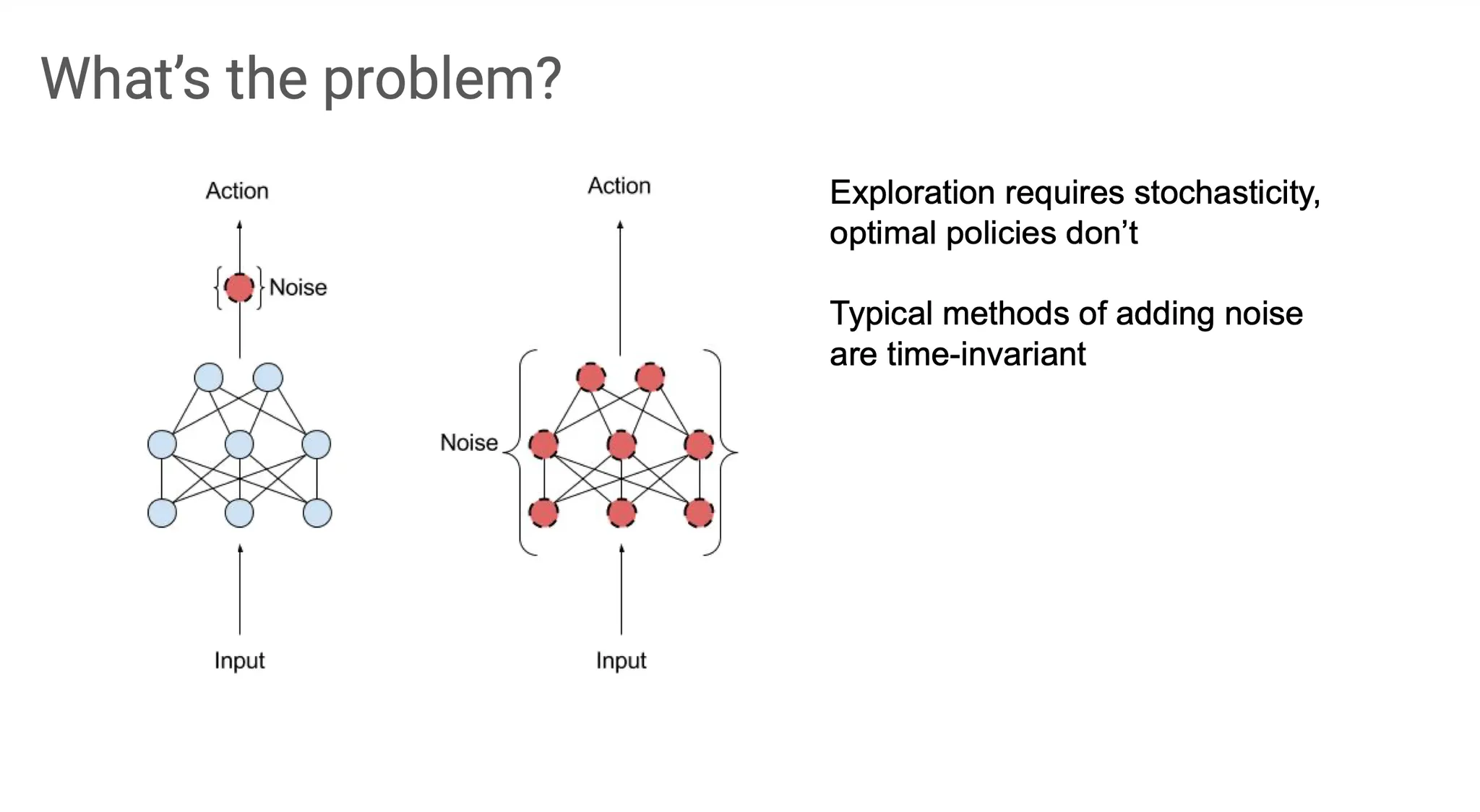
즉, exploration 과정에서는 일종의 stochasticity가 필요한 반면 optimal policy는 deterministic하다. 단순한 방법으로는 하나의 policy에 성격이 다른 두 개를 동시에 represent 하기는 어렵다.
그리고 이 stochasticity를 반영해주기 위해 noise를 넣어주어야 하는데, 일반적으로 noise를 가해주는 작업은 time-invariant 하다. 따라서 sequential learning이 필요한 RL에 그대로 적용하기가 어렵다.
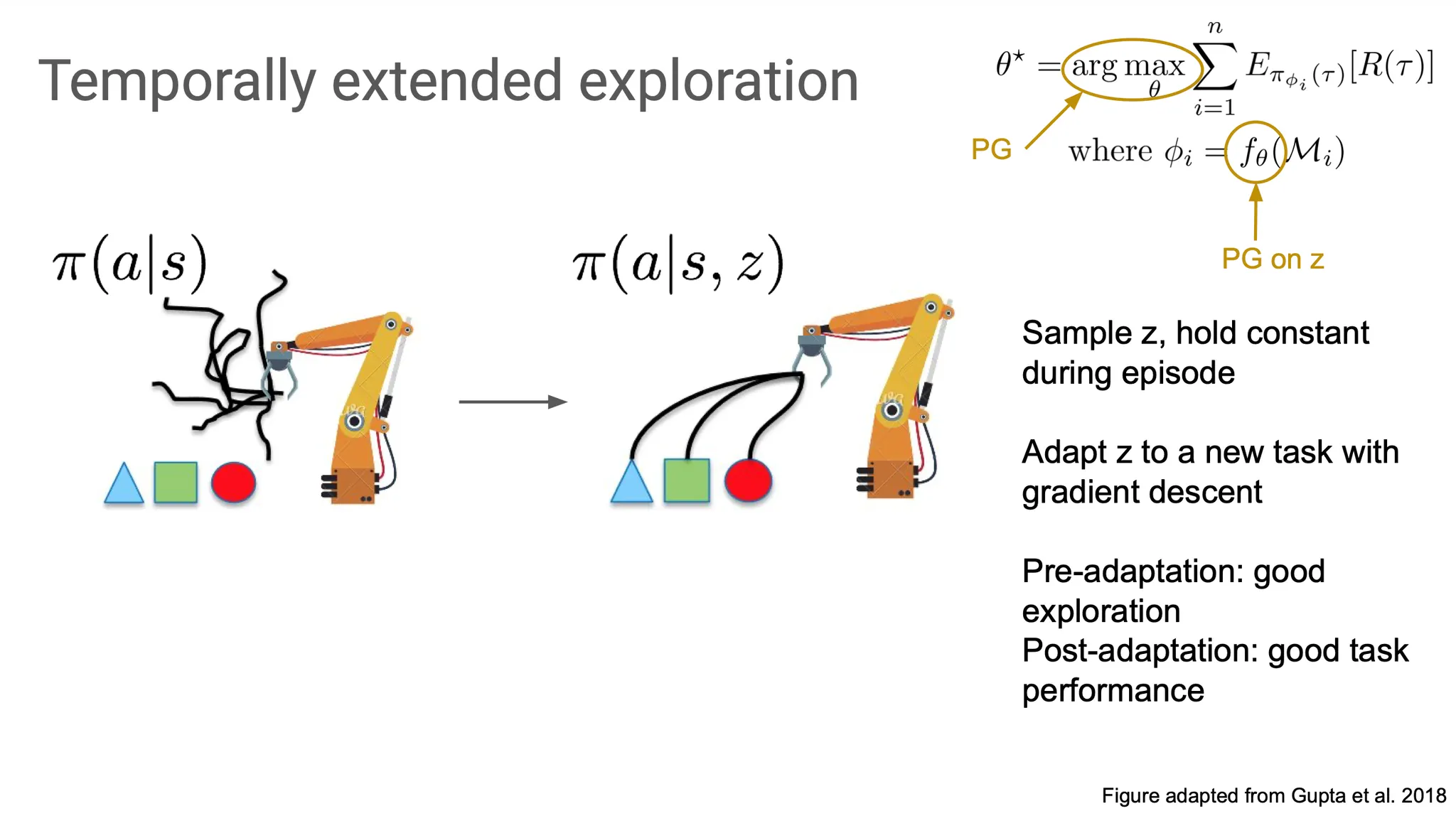
따라서 ‘time’을 explicit하게 반영할 수 있는 방법을 도입해 볼 필요가 있다. 그 방법 중 하나로 latent variable 를 이용해 policy를 augment 할 수 있다.
를 sampling하여 한 episode에서 그 를 유지하여 meta training 과정에서 task에 유용한 optimal trajectory를 제공할 수 있도록 만들 것이다.
즉, outer loop은 여전이 policy gradient를 사용하고, inner loop은 에 대한 policy gradient를 수행해서 task performance를 끌어올린다.
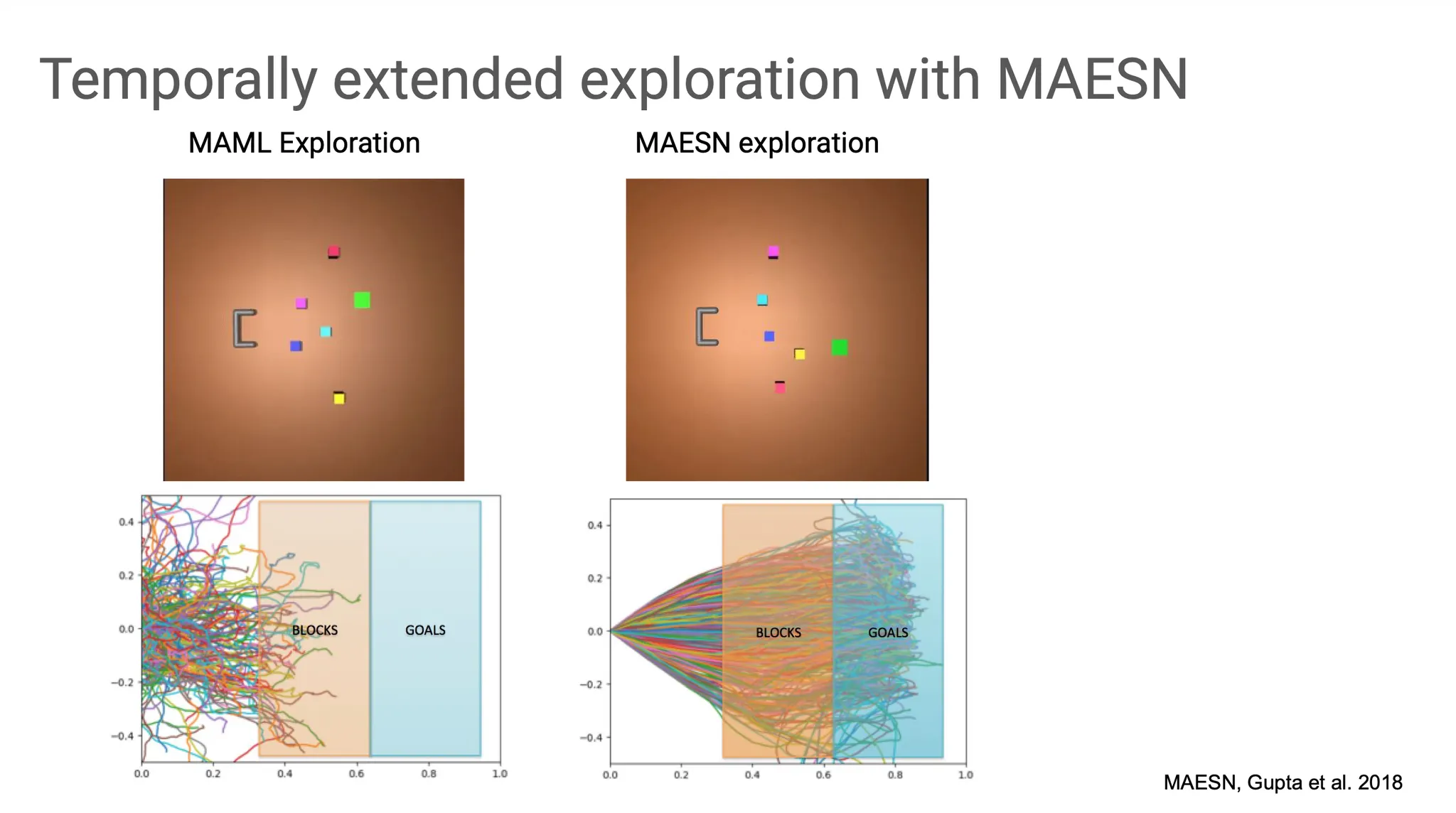
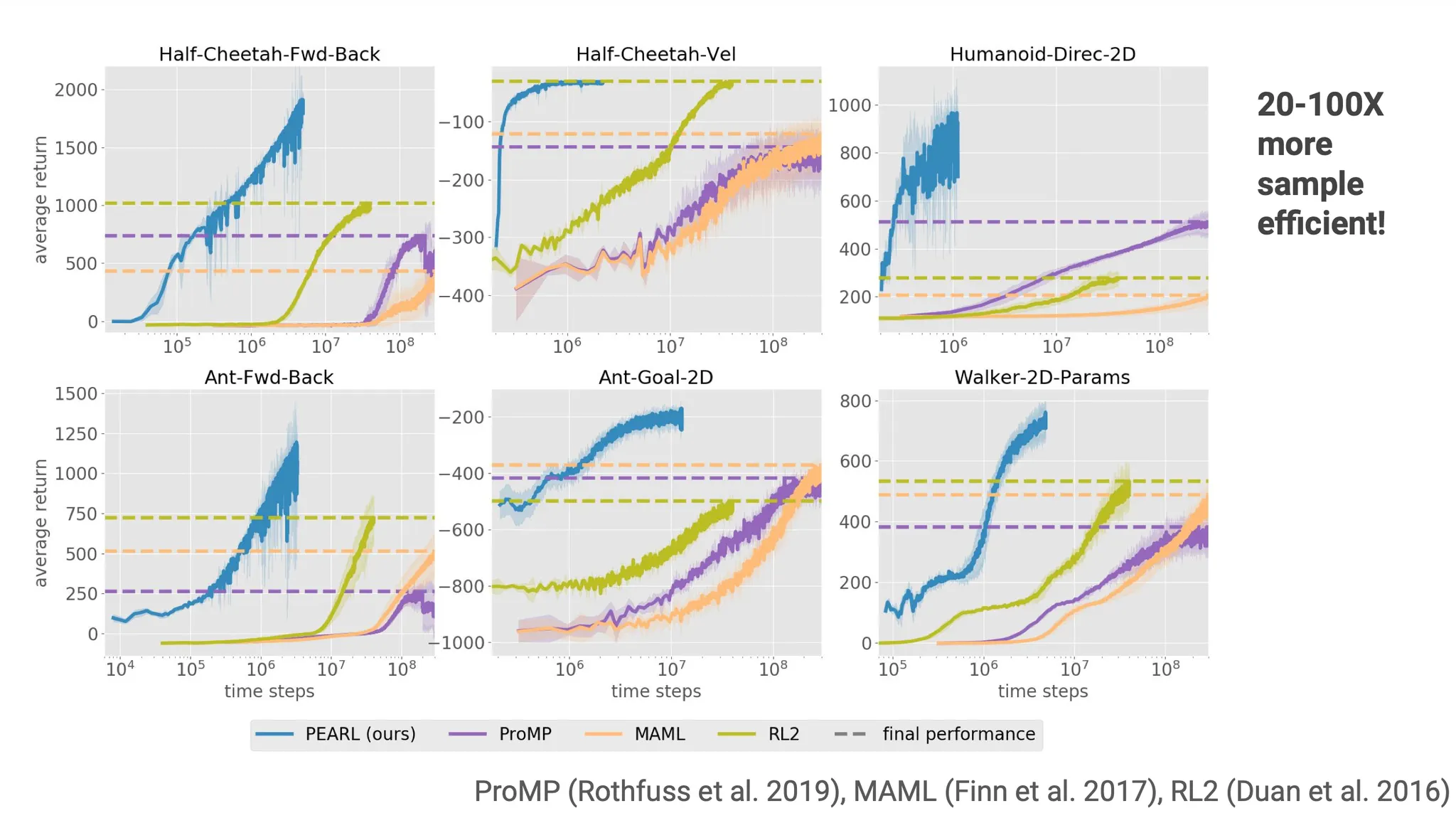
이 방법은 MAESN 이라고 불리고, 특정 task에서 MAML과 비교했을 때 훨씬 효율적이고 효과적인 학습을 하는 것으로 보인다. MAML은 random하고 incoherent 한 학습을 진행하는데, MAESN은 latent variable을 도입해 task distribution을 반영할 수 있어서 각 task(특정 block을 오른쪽으로 밀어내는)에 대한 정보를 습득한 채로 학습이 진행된다.
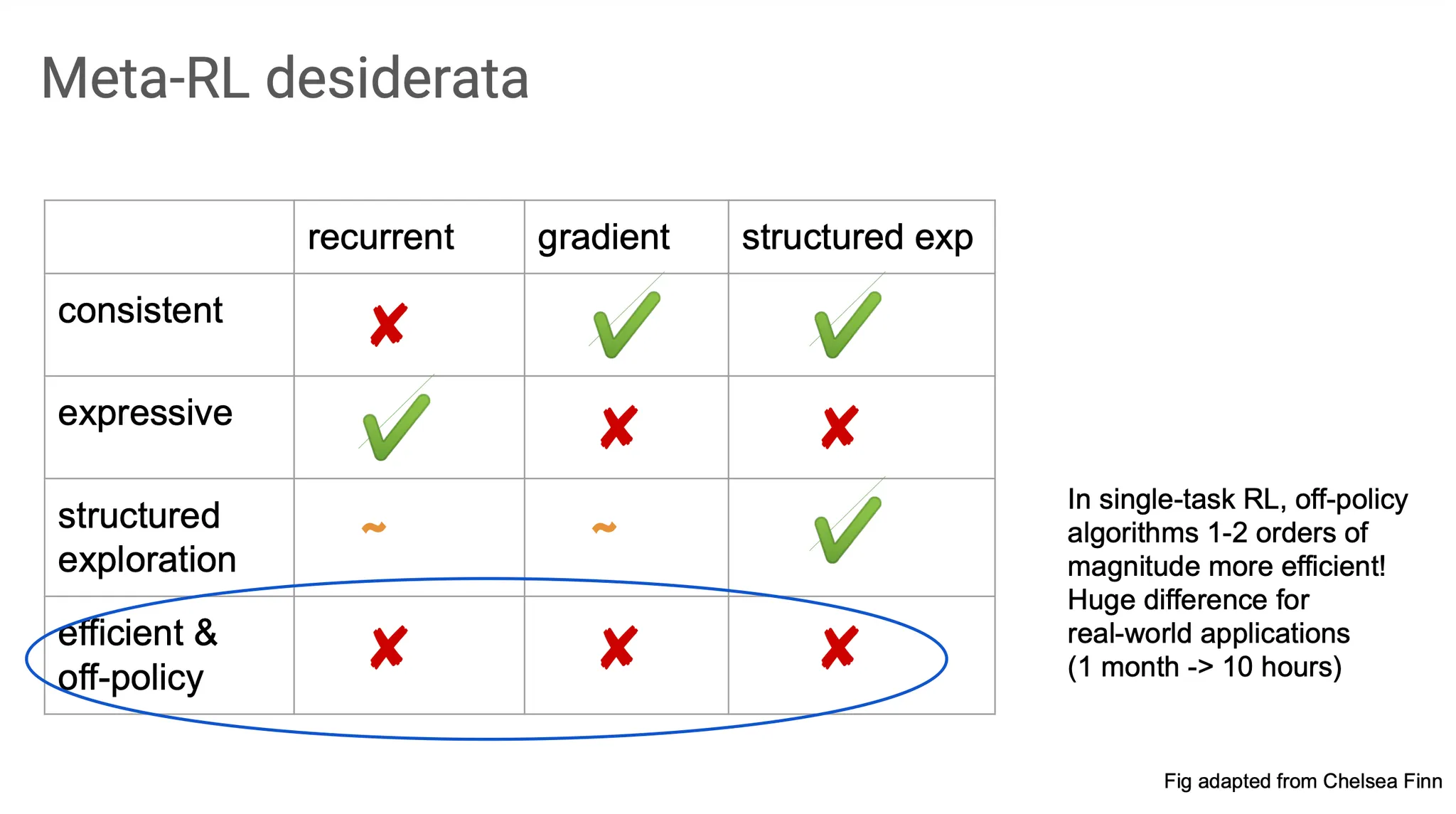
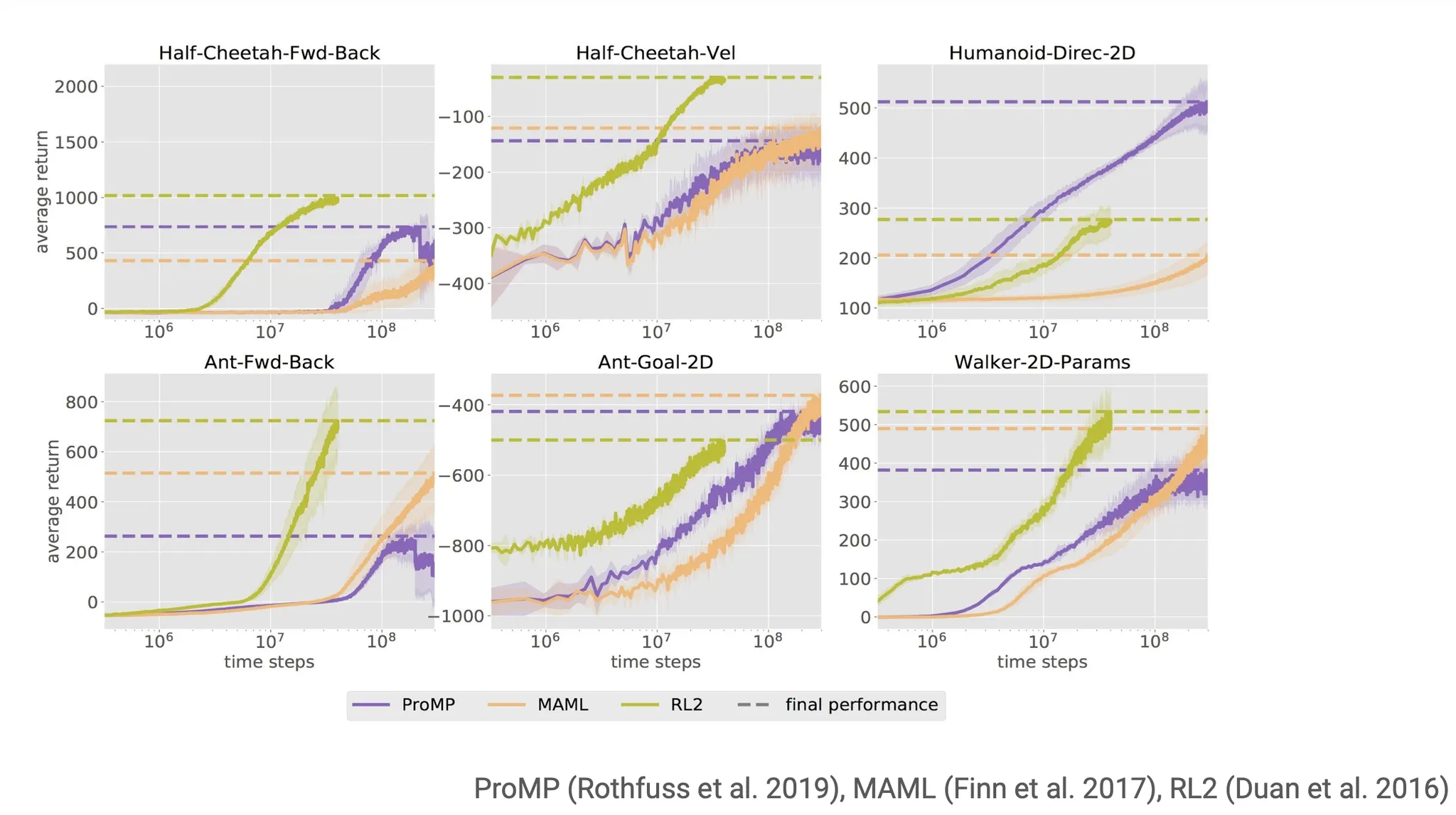
정리해보면, recurrent method는 consistent 하지는 않지만 expressive 했다. Gradient method(e.g. MAML)은 consistent하지만 expressive 하지는 않았다. Structured exploration(e.g. MAESN)은 여기에 task distribution을 반영해주는 latent variable을 사용했다.
위 방법들 모두 on-policy algorithm인데, 이는 data를 효율적으로 사용하지 못 하는 문제가 있다. 이를 어떻게 해결할 수 있을까?
먼저 왜 meta-RL에서 off-policy로 학습하는게 어려울까?
Meta learning은 meta training과 meta test 시의 조건이 동일해야 한다. 그런데 off-policy로 학습하려면 agent가 특정 episode에 대해 학습할 때는 on-policy data를 수집하지만 meta-training 시에는 off-policy data도 함께 이용해야 한다. 이는 꼭 off-policy meta-RL 뿐만 아니라 일반적으로 off-policy algorithm을 학습하는 것이 어려운 이유이기도 하다.
Off-policy meta-RL을 위한 한 가지 방법으로 PEARL 이라는 모델을 예시로 들자.
PEARL 읽어보기!!
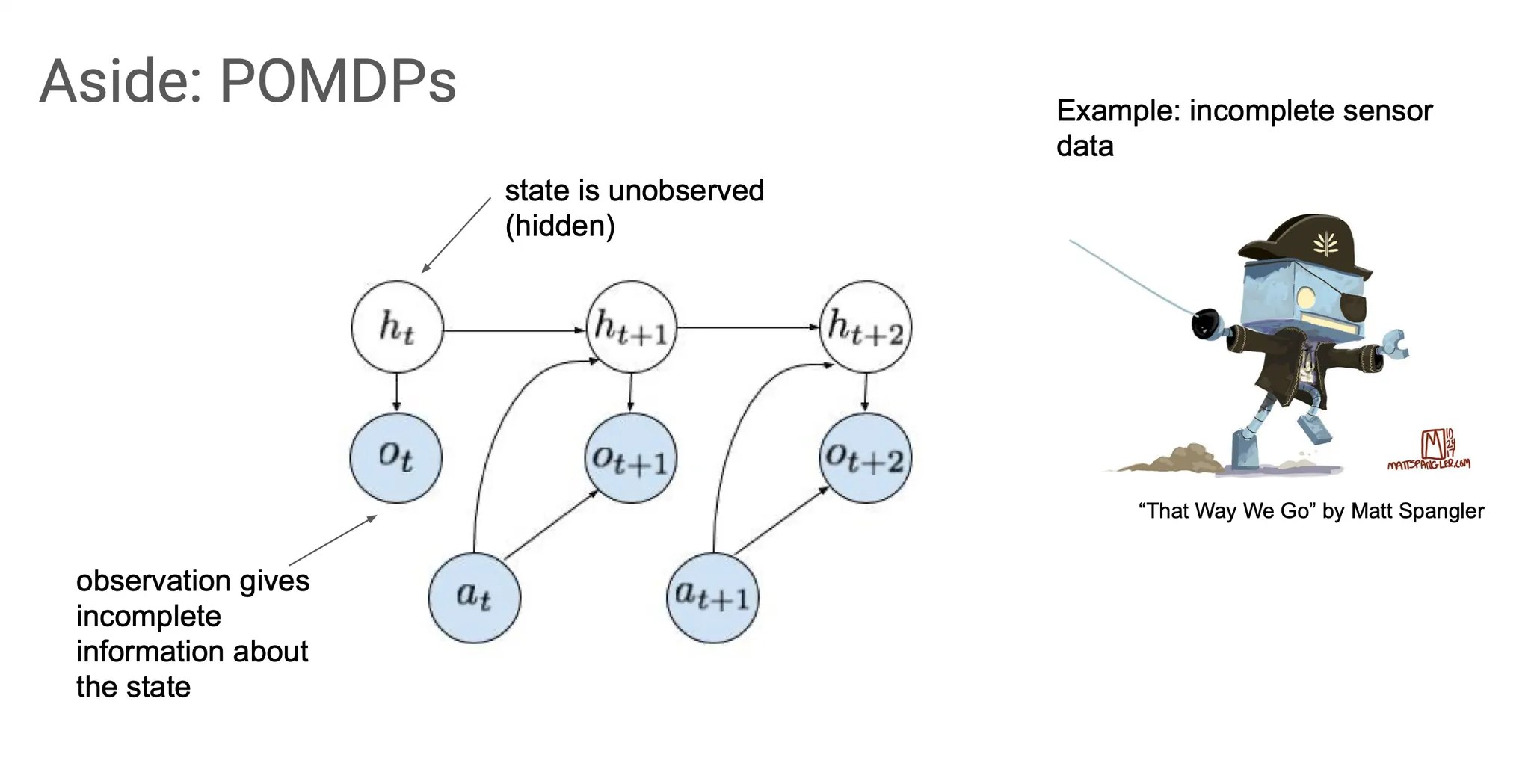
POMDP(partially observed MDP)는 우리가 볼 수 없는 hidden state에 대한 정보를 주는 observation이 그 state에 대한 정보를 충분히 못 담고 있는 상황을 말한다. 예를 들어, sensor data가 부족하거나, 속도를 알아야 하는데 위치만 관측된다거나 하는 상황이다.
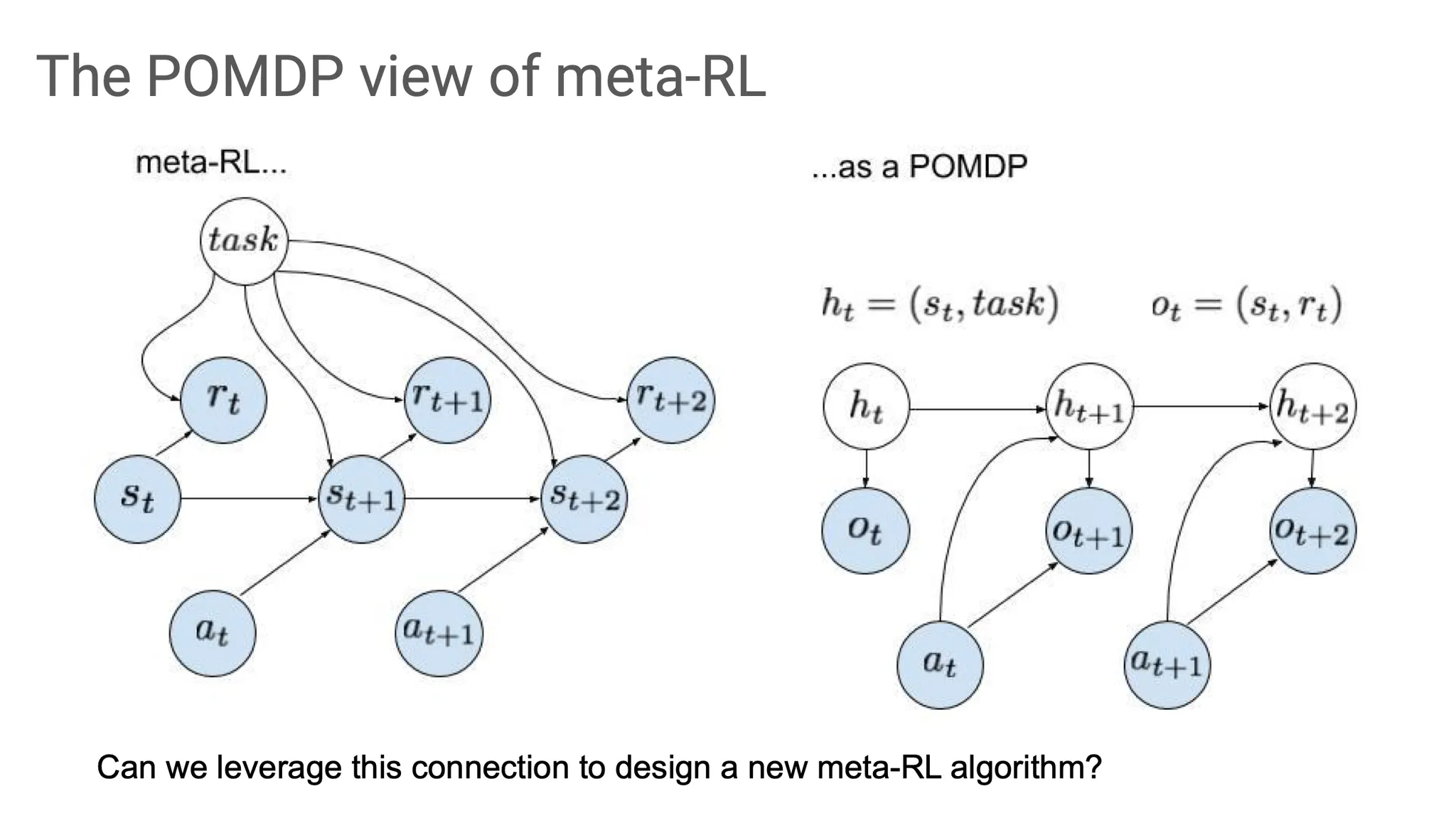
일반적으로 meta-RL은 왼쪽처럼 task dependent한 computation graph를 그릴 수 있다.
하지만 POMDP에 맞게 조금 바꿔보면, true state롸 task를 concatenation한 것을 hidden state라고 부르고, observation을 state와 reward의 concatenation이라고 생각해볼 수 있다. 여기서 state의 일부를 관측하지 못하는 상황도 있을 수 있지만, 우선 편의를 위해 state는 관측했고, task만 모르는 상황을 가정해보자.
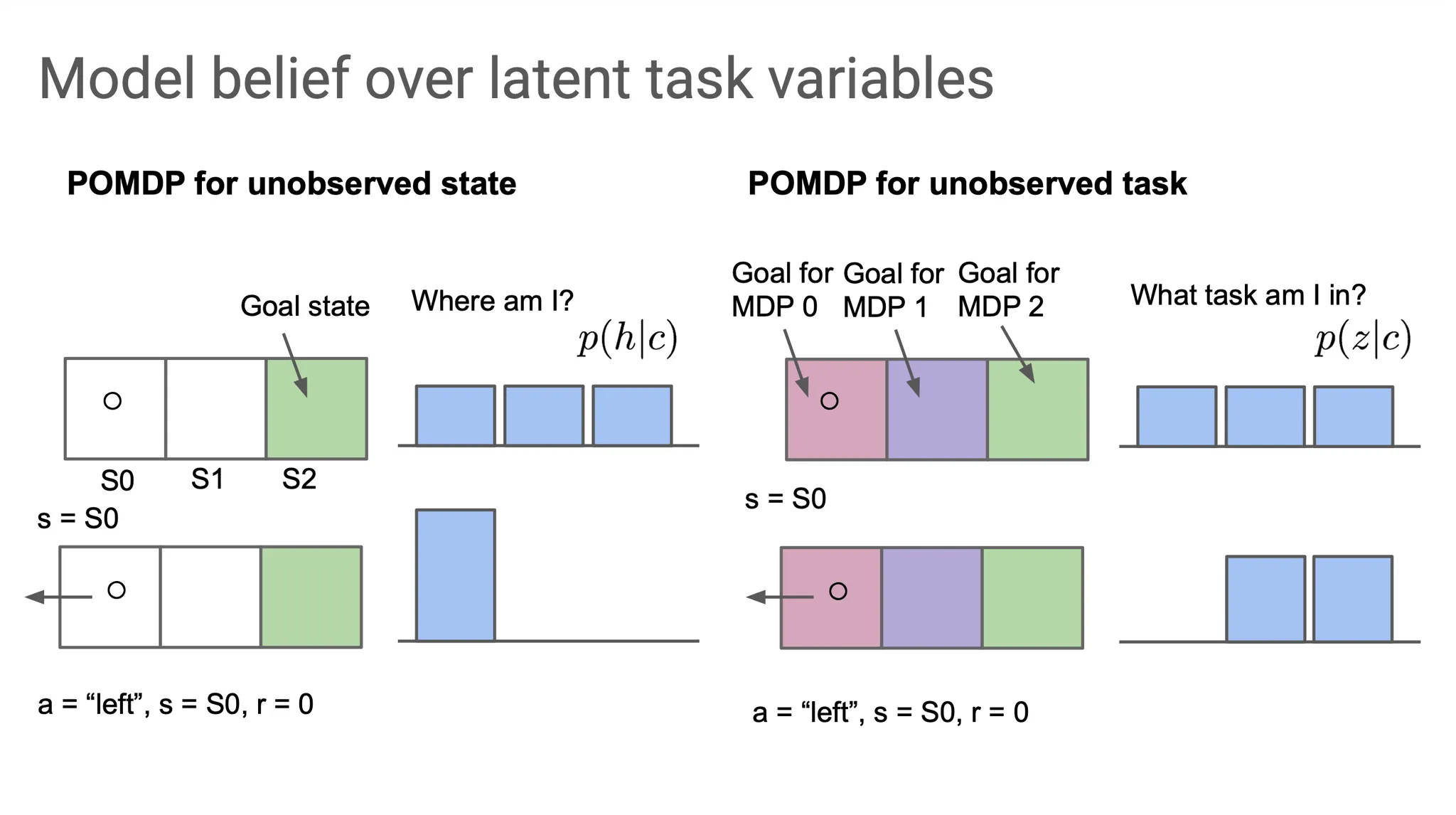
예를 들어, S2에 도달하는 것이 goal인 task(하지만 어떤 task인지 agent는 모르는 상황)에서 초기 state는 S0로 알고 있다. 그런데 왼쪽으로 가는 action을 취하니, state가 S0임이 관측되었고, reward는 0이었다.
이 경우, task는 두 가지 option으로 추려지게 된다. 즉, S1에 도달하거나, S2에 도달하는 것 둘 중에 하나일 것이다.
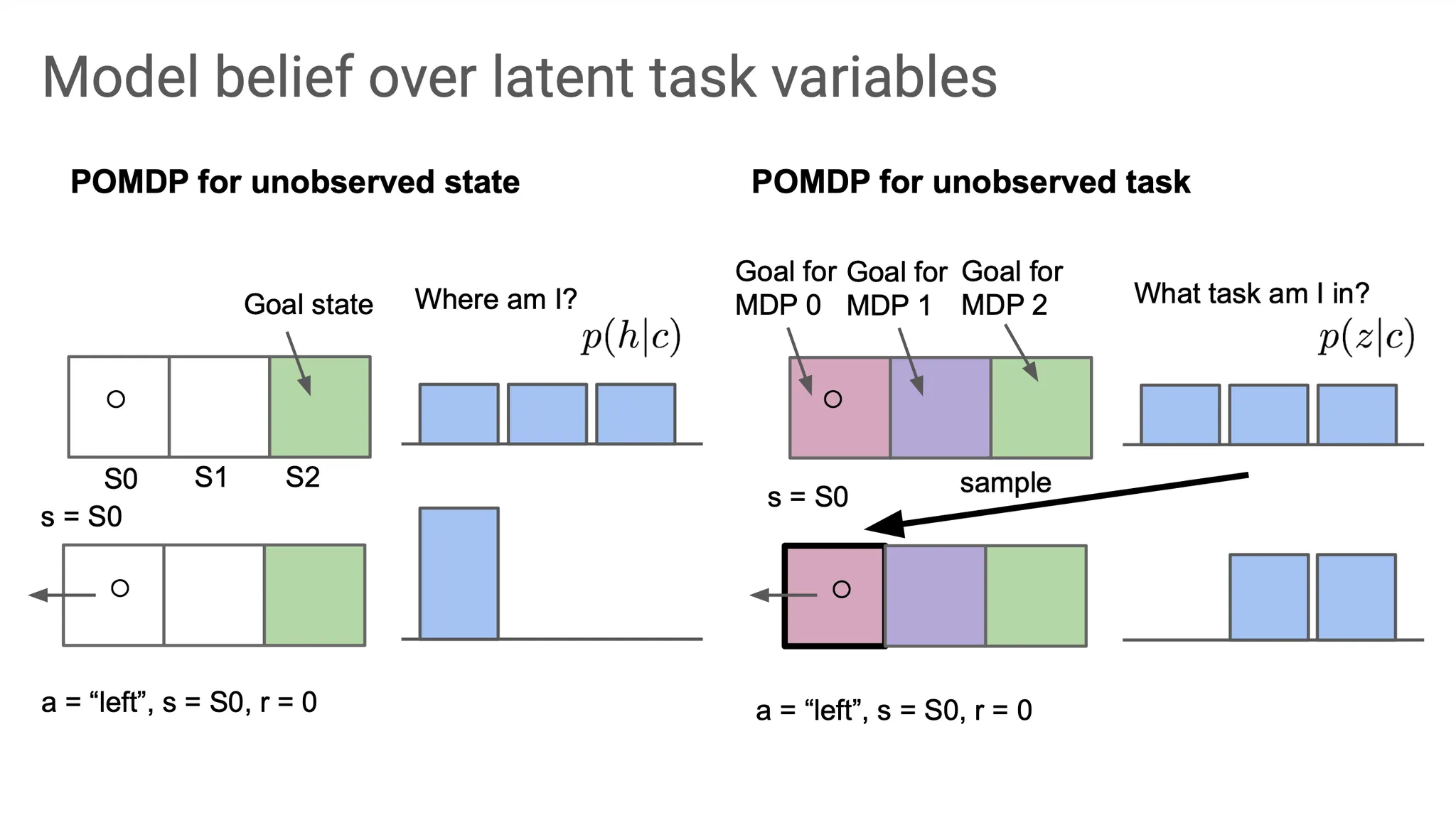
이런 식으로 exploration을 하다보면, 어떤 task에 속해있는지 점점 더 정확하게 알 수 있을 것이다. 이런 방법을 posterior sampling 또는 Thompson sampling이라고 부른다.
좀 더 자세히 말하자면, 우선 현재 state에서 sampling을 해보고 그 sample(S0)이 true 라고 가정을 해본다. 그에 맞는 action(여기서는 왼쪽으로 가서 그대로 S0에 있도록)을 취해보고, reward(이 상황에서는 0)를 얻는다. 이런 식으로 수행해보면 현재 어떤 task에 있는지의 확률을 의미하는 belief distribution이 update 될 것이다.
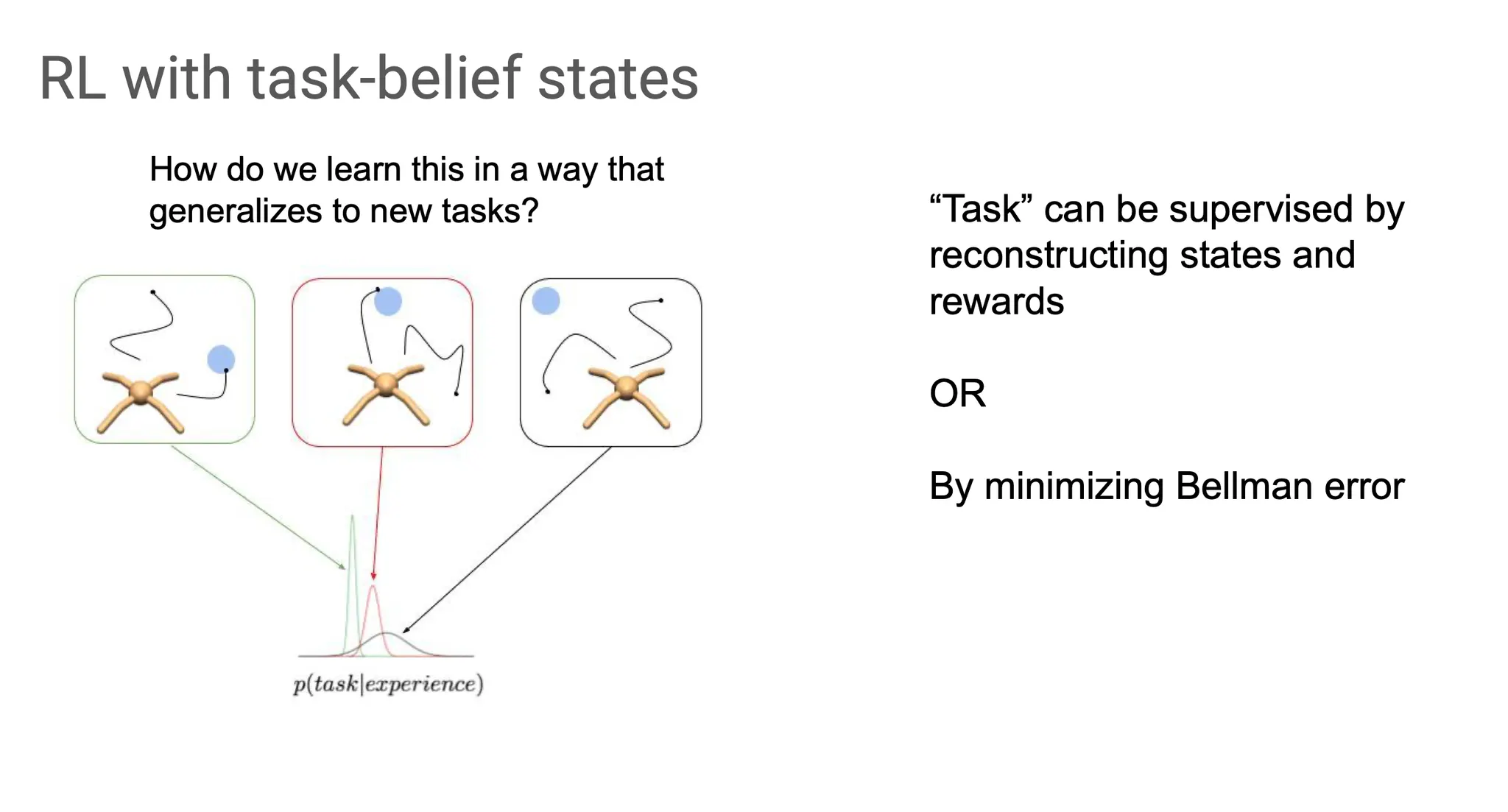
Task-belief 를 update하는 과정에 supervision을 어떻게 줄 수 있을까?
1.
Task에 대한 정보를 찾아감에 있어서 state와 reward를 다시 조정해보거나
2.
Bellman error를 최소화해볼 수 있을 것이다.
Algorithm을 구축하기 위해 수식으로 나타내어보면, 우리는 어떤 task인지 알기 위해 매번 posterior belief distribution 을 update한다. 이때 는 context, 즉 adaptation data를 의미한다.
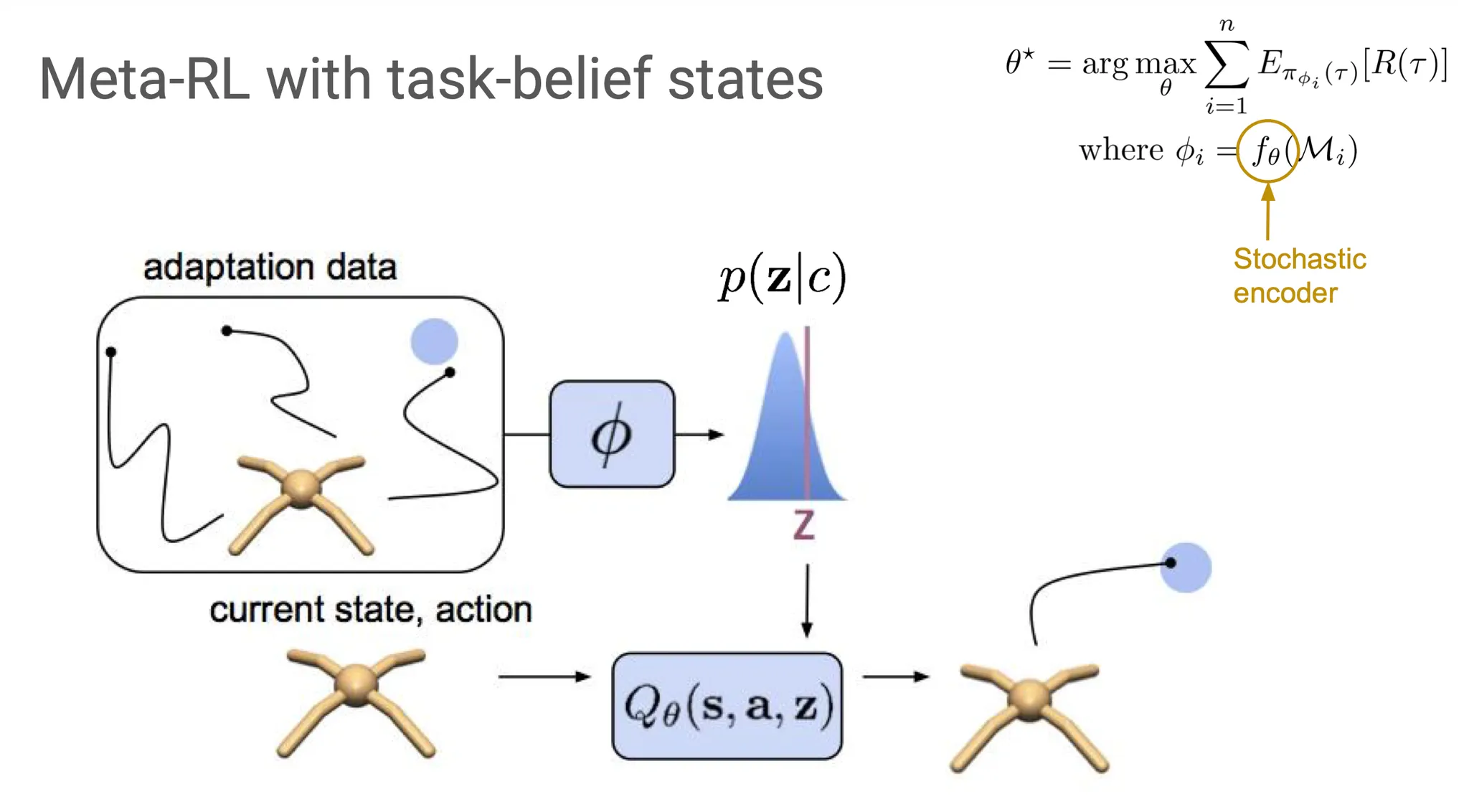
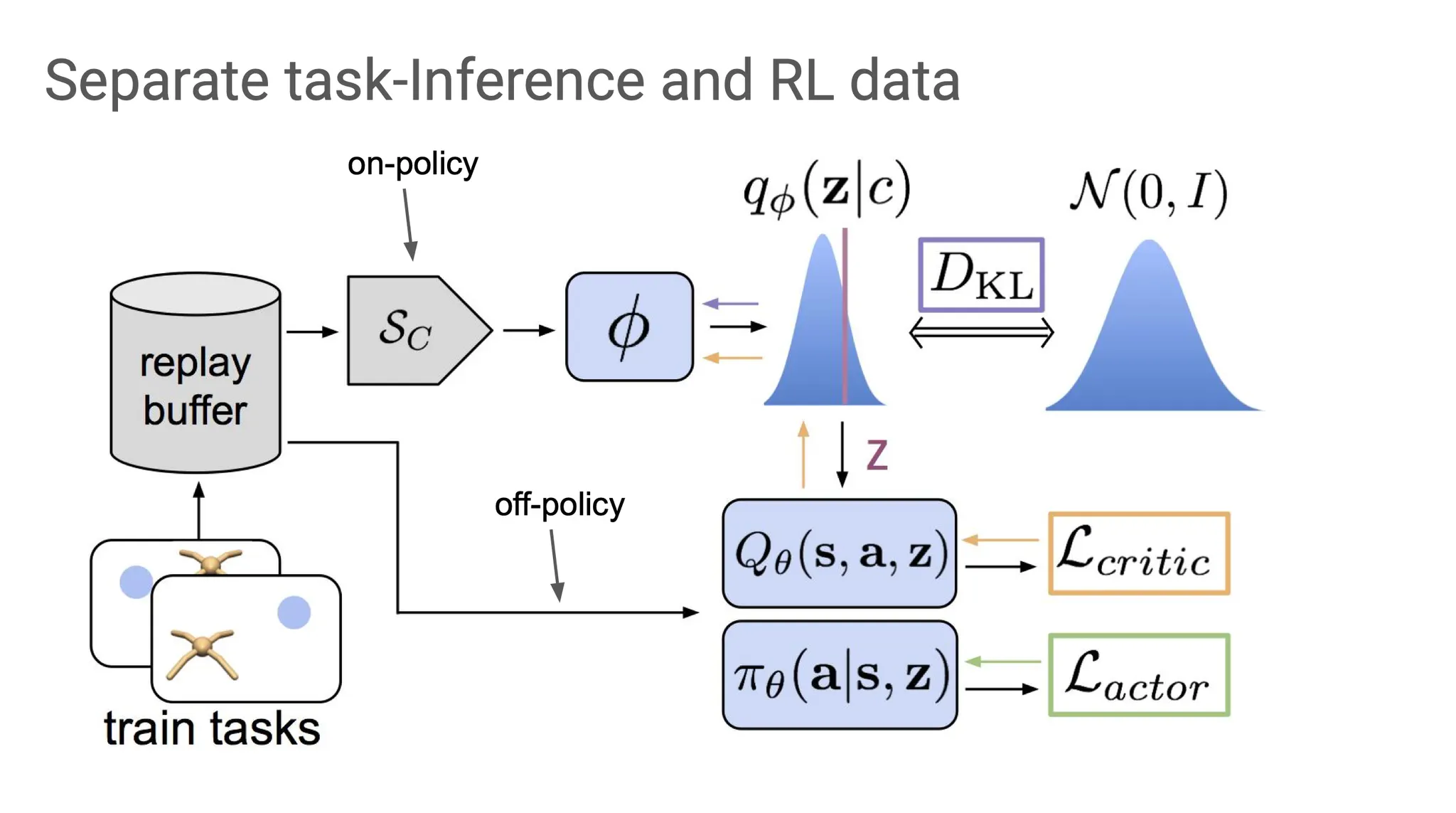
Adaptation data로부터 가 그 상황을 학습하고 가 를 update한다. Update된 에서 data를 generation하여 exploration한다.
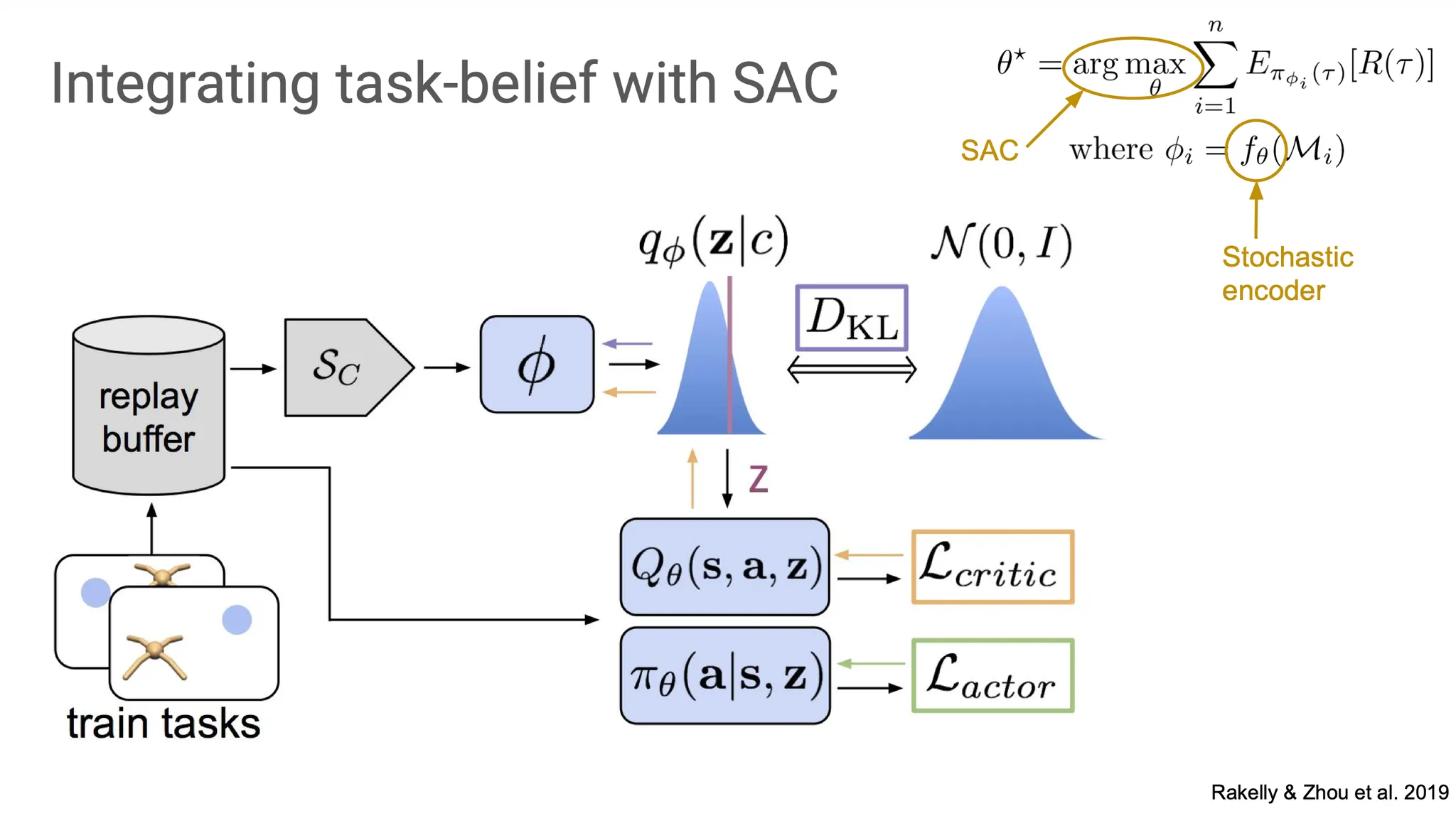
오른쪽 위의 general RL framework으로 설명해보면, 이제 의 는 일종의 stochastic encoder로, sampling을 하는 부분이 된다.
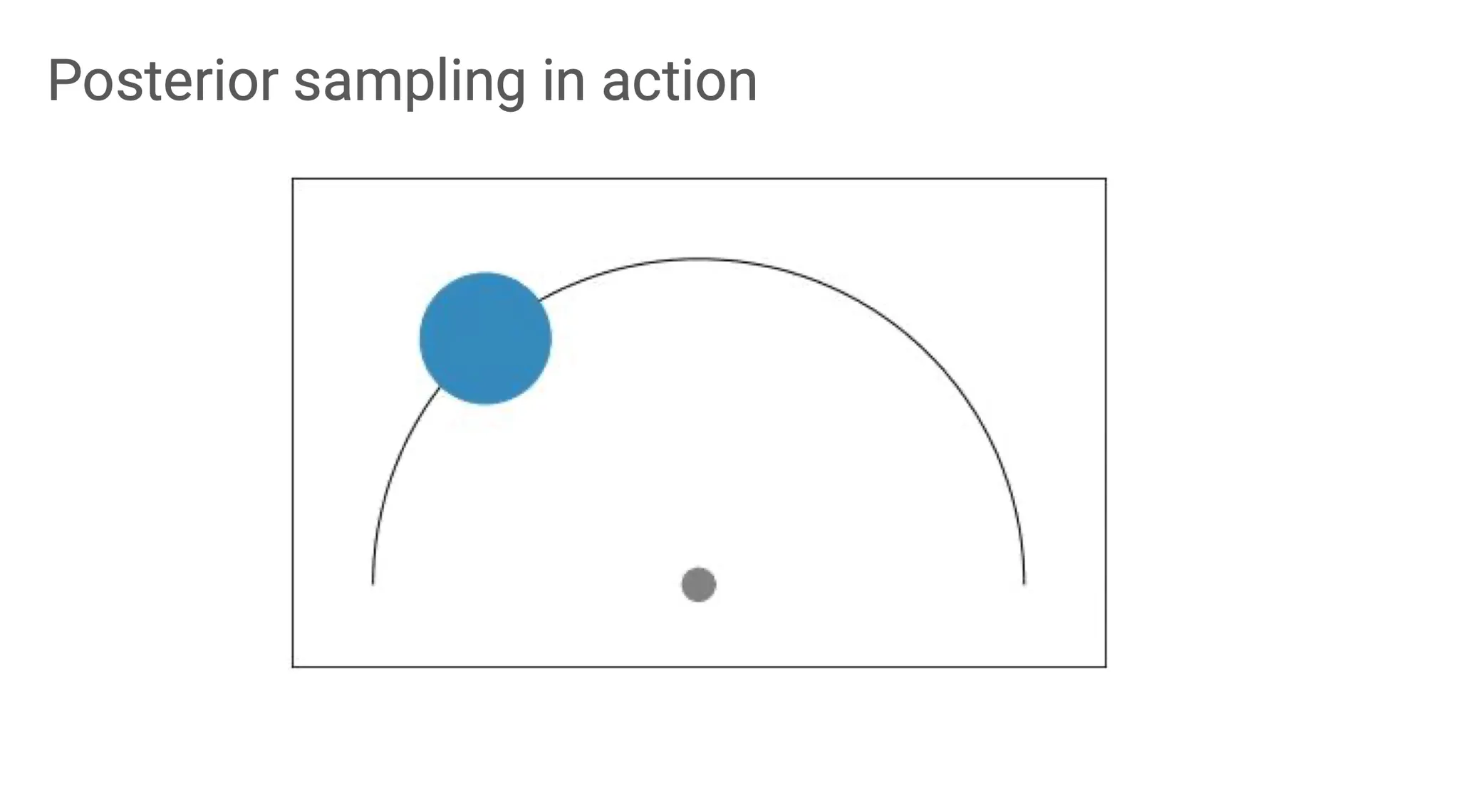
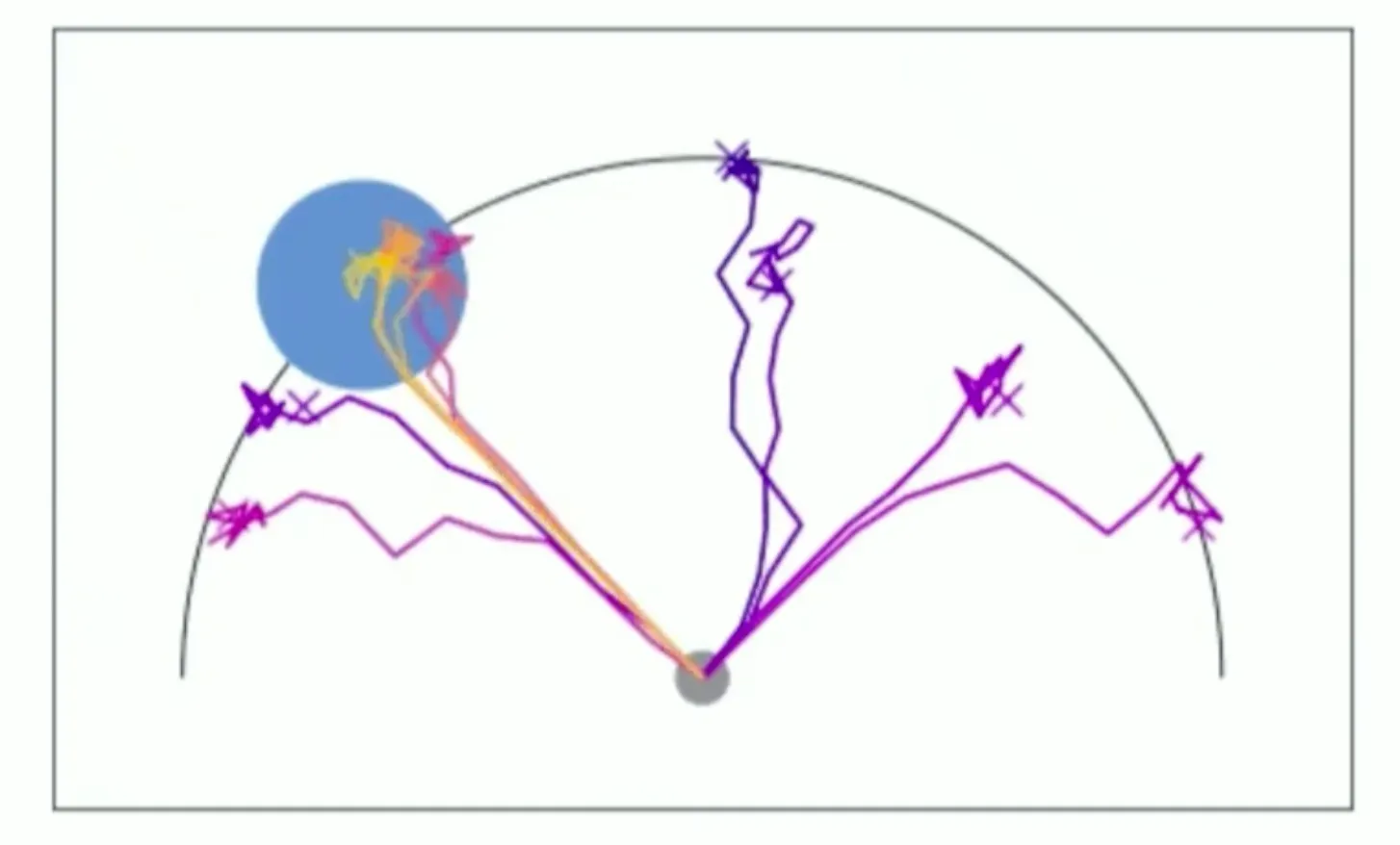
예를 들어보면, 회색 area에 존재하는 agent가 파란 area에 도달해야 하는 상황이다. 계속 탐색을 하되, 이전의 경험을 기억하고, belief distribution에 따라 다른 곳을 탐색해보도록 guide할 수 있다.
좀 더 formalize해보면, true 를 계산하는 것은 intractable하다. 그래서 대신 variational inference를 사용한다. 따라서 우리는 로 approximation 할 것이고, 이 과정의 parameter가 (neural network)이다.
ELBO의 첫 번째 term은 likelihood term이다. 이 likelihood term을 maximize하는 것이 목적이고, 이번에는 Bellman error를 약간 뒤틀어서 likelihood 형태로 사용한다.
ELBO의 두 번째 term은 regularization term이다. Likelihood를 maximize할 때, 최소한의 정보만 전달해줘도 되도록 guide하는 condition을 부여하는 부분이다.
그럼 stochastic encoder 는 어떻게 디자인할까?
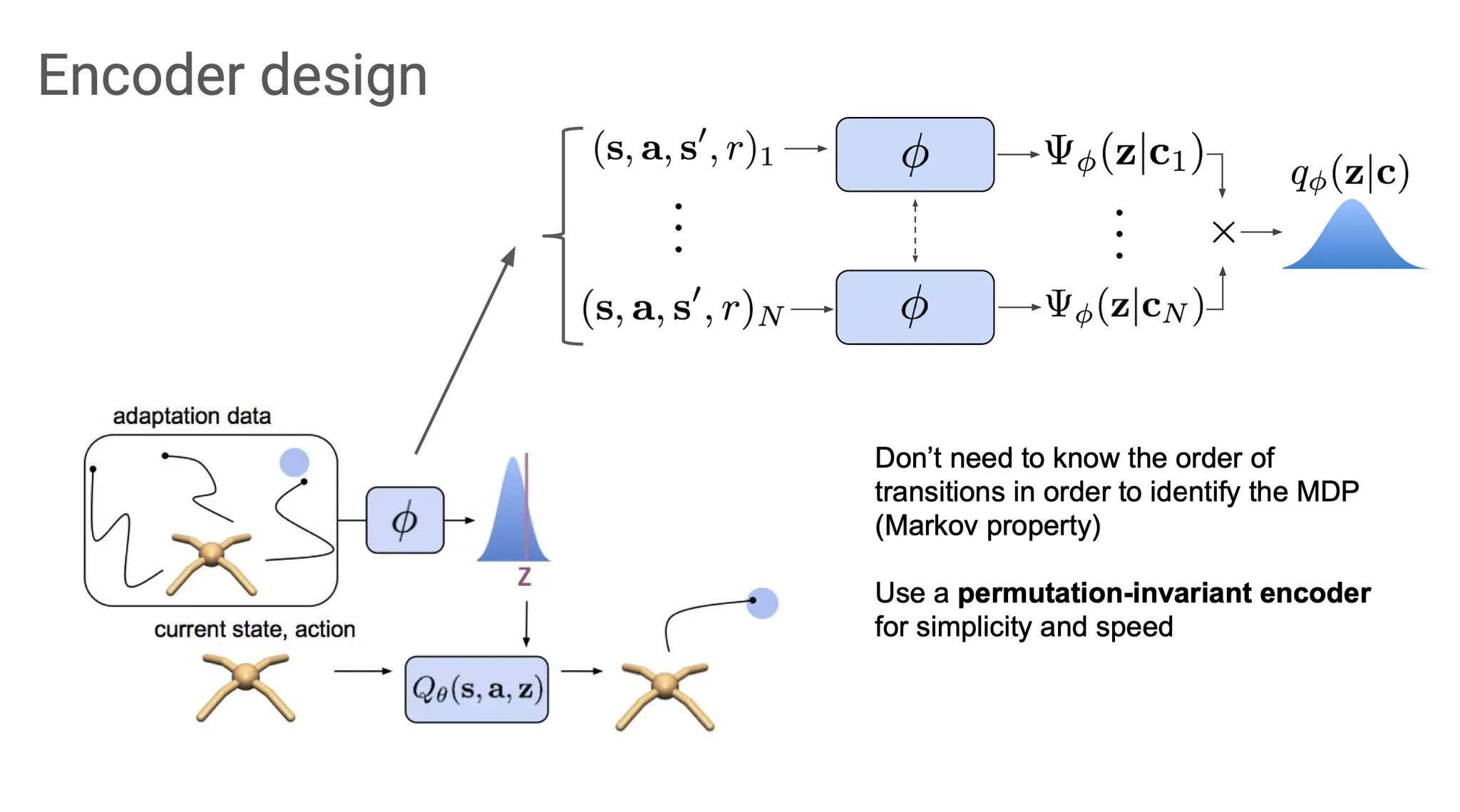
우리의 목적은 task에 대한 belief를 infer하는 것임을 기억하자. 그리고 참고로 Markov property로 인해서 굳이 context 들을 순서대로 넣어주지 않아도 된다.
이 context들을 각각 따로 에 통과시켜 Gaussian factor를 각각 만들어내고, 그들을 곱해서 Gaussian posterior 를 만들어낸다. 여기서 Gaussian을 쓰는 이유는 reparametrization이 쉽기 때문이다.
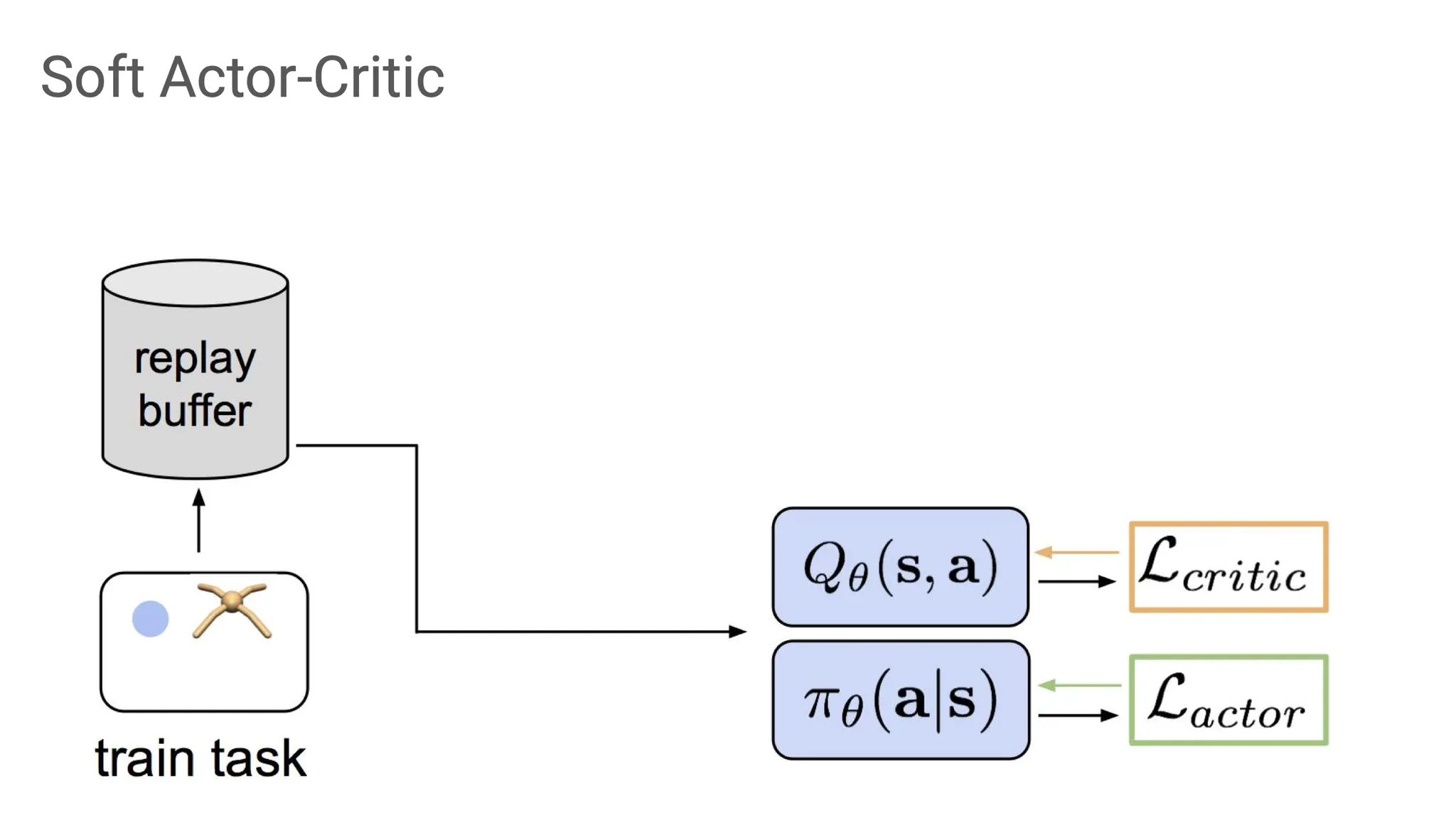
Soft actor critic(SAC)에 대해서 살펴보자.
Soft 하다는 말은 reward를 maximize 할 때, policy의 entropy도 고려하자는 의미이다. 즉, 그냥 reward만 maximize하면 exploitation만 하기 때문에 exploration을 더 하도록 guide하는 것이다.
Actor-critic은 actor와 critic 모두를 modeling하는 것인데, 여기서 critic은 Bellmann error 가 반영된 Q function이고, actor는 높은 Q value와 entropy를 주는 policy이다.
Diagram으로 나타내보면, task를 수행하면서 나오는 data들은 replay buffer에 담기고, 그 정보를 사용해 critic과 actor를 모두 학습한다.
Task belief를 학습하는데 있어 SAC를 사용하면,
먼저 belief posterior를 approximate해서 sampling 하고, 그 sample들을 actor와 critic에 전달한다. 즉, actor와 critic은 MDP의 original state와 의 concatenation 한 vector를 전달 받는다.
그럼 왜 meta-RL을 POMDP로 보고 task에 대한 belief를 estimate 하는 것이 off-policy meta-RL에 도움이 될까?
이 방법은 replay buffer의 data를 task를 infer하는 것과 actor/critic을 학습하는 것으로 구분할 수 있다. Adaptation은 on-policy로, actor-critic 학습은 off-policy로 학습한다. 즉, task-specific하지 않은 정보(e.g. 걷는 방법 자체)는 off-policy로 학습하고, task(e.g. 뒤로 가기, 옆으로 가기)를 알아내기 위한 정보는 on-policy로 학습한다.
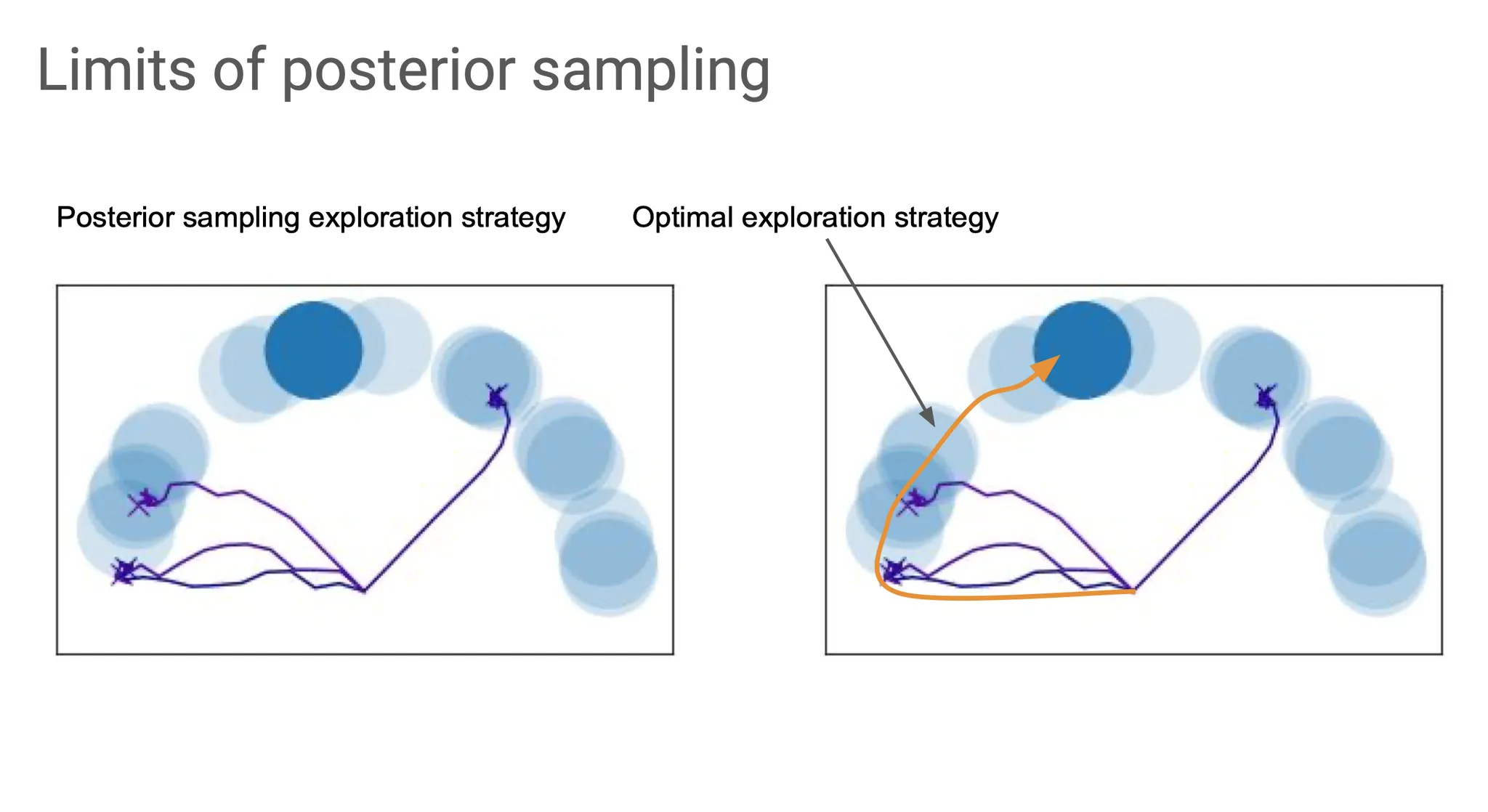
그렇다고 posterior sampling이 항상 좋은 것은 아니다. 위 그림의 상황에서 진한 파란색의 원으로 가는 optimal exploration 전략은 사실 맨 처음 잘못 도달했던 곳에서 그냥 쭉 arc를 따라서 목표 지점으로 가는 것인데, posterior sampling은 이렇게 explore 할 수 없다.
MAESN 같은 경우는 adaptation 한 후에는 prior distribution에서 각 task마다 서로 멀리 떨어진 posterior distribution을 갖게 되고, off-policy인 PEARL은 task의 공통점을 반영하여 학습하기 때문에 서로 그리 멀리 떨어지지 않는다.