Search

[CS224W] Lecture 11

Recap

Knowledge graph completion task
•
큰 KG가 주어졌을 때, KG completion을 어떻게 할 수 있는가?
더 구체화해보면, (head,relation)(head, relation)이 주어지고, missing tailtail을 맞추는 task라고 할 수 있다.

Today: Reasoning over KGs

•
목표: KG에서 multi-hop reasoning을 어떻게 할 것인지에 대해 배운다.
◦
Answering multi-hop queries
▪
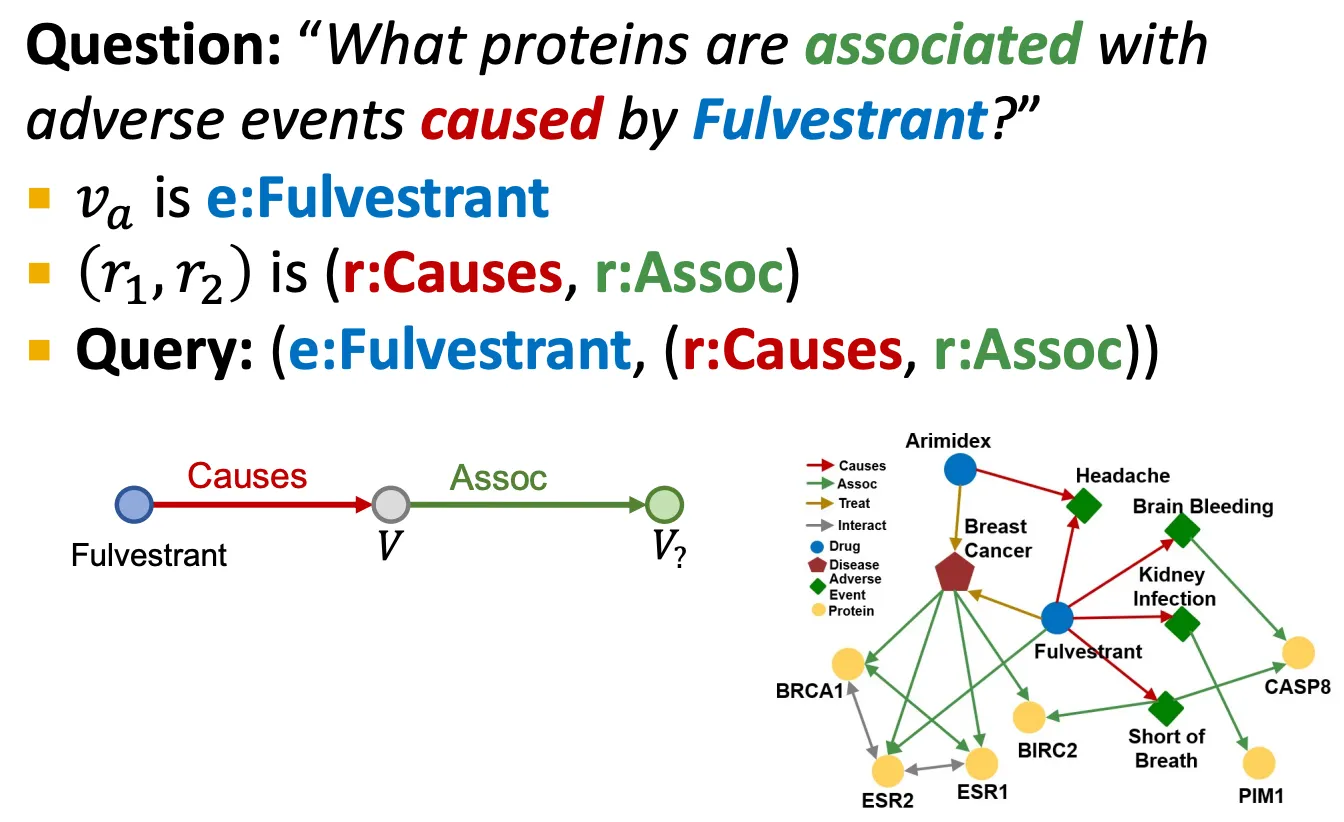
Path queries
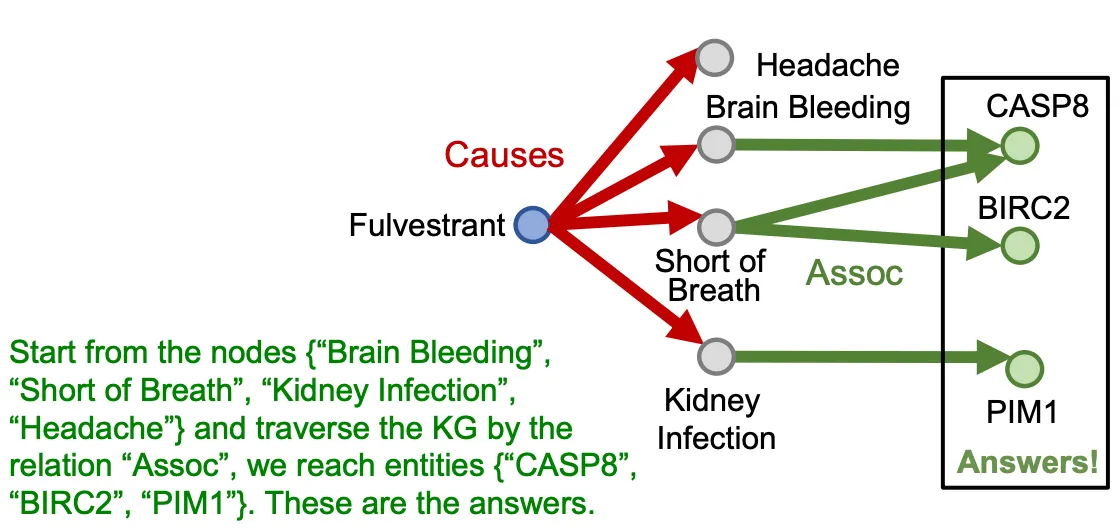
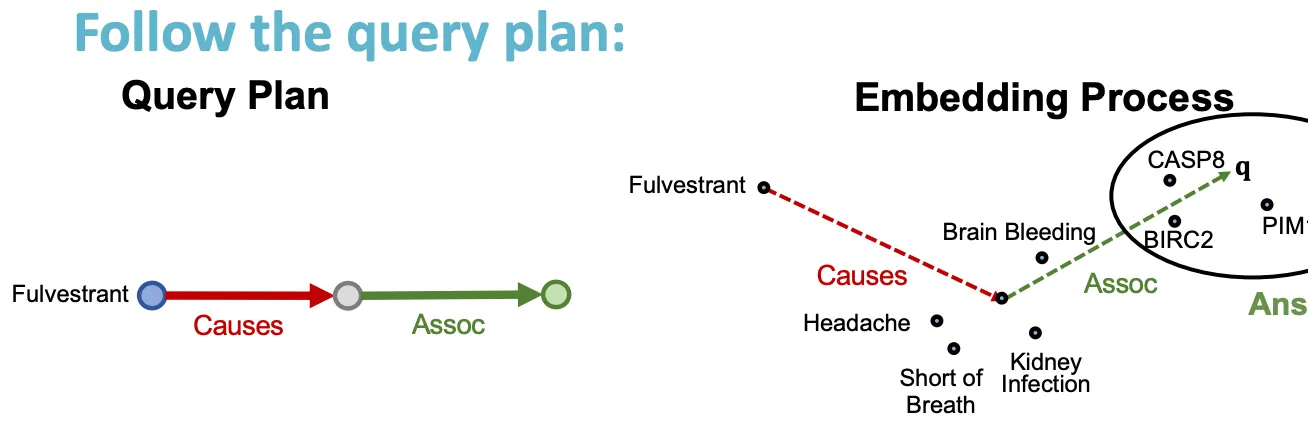
e.g.) Fluvestrant에 의해 야기된 부작용과 어떤 단백질이 연관이 있는가? → (e: Fulvestrant, (r: Causes, r: Assoc))
▪
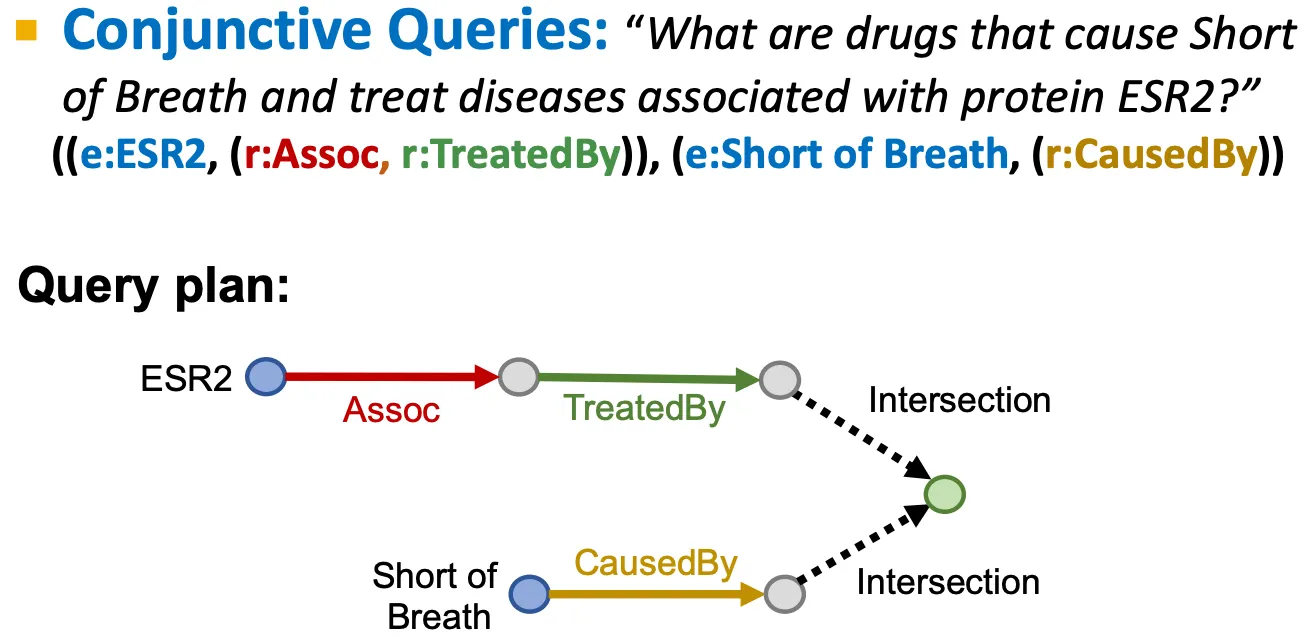
Conjunctive queries
e.g.) Breast cancer를 치료하기도 하고, 두통을 유발하기도 하는 약물은 무엇인가? → ((e:Breast Cancer, (r:TreatedBy)), (e:Migraine, (r:CausedBy)))
◦
Query2box
Predictive one-hop query
•
Is tt an answer to query (h,r)?(h,r)?
e.g.) 약물 Fulvestrant에 의해 야기된 부작용은 어떤 것인가?

Path queries

•
Path를 따라 relation들을 추가하여 generalize 한다.
•
nn-hop path query qq = (va,(r1,...,rn))(v_a, (r_1, ..., r_n))
◦
vav_a: anchor entity
◦
query qq에 대한 답은 [q]G[q]_G로 표시한다.
Traversing knowledge graphs
•
Path query에 대한 답은 KG를 traverse 하여 얻는다.
•
하지만 KG는 incomplete하고, 아마 절대 그 어떤 상태도 complete 하다고 단정할 수는 없을 것이다.
◦
missing relation, missing entity 등이 너무 많다.
•
따라서 모든 entity에 대한 답을 traversing 하면서 얻기는 어렵다.
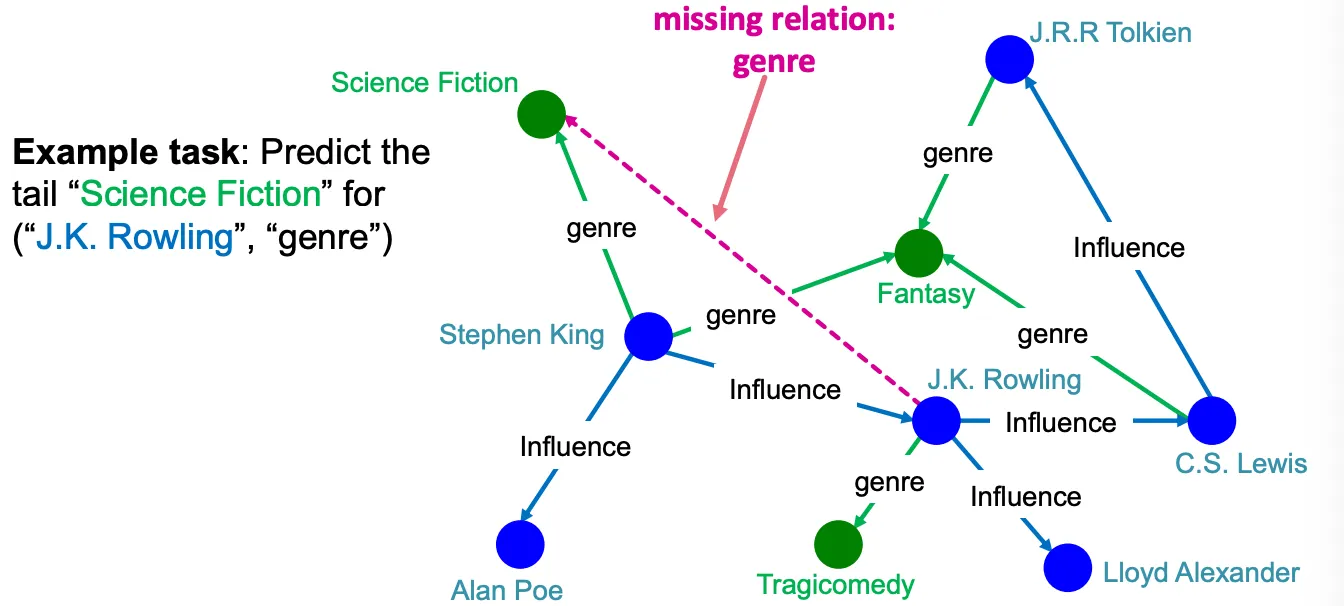
Can KG completion help?
•
그렇다면 먼저 KG completion을 어떻게든 수행하고, completed KG를 traverse 하면 괜찮을까?
그렇지 않다. Completed KG는 매우 dense해서 time complexity가 O(dmaxL)O(d^L_{max})인 상황에서 계산이 어렵다.
•
따라서 implicit 하게 impute 하여 incomplete KG인 상황에서도 predictive query에 대한 답을 얻어야 한다.

Answering Predictive Queries on Knowledge Graphs

General idea
•
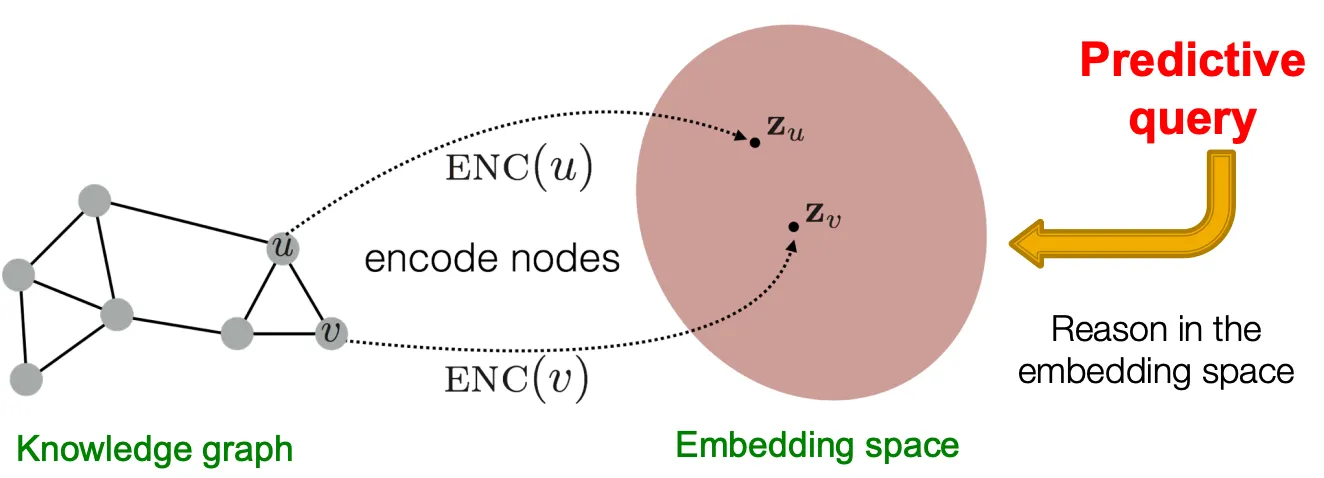
Query를 embedding space로 mapping 하고, 그 space 상에서 reasoning을 하게 하자!
◦
Euclidean space에서 하나의 점으로 query를 embed 하고, answer node가 그 query에 가깝게 위치하도록 한다.
◦
Query2Box: query를 hyper-rectangle (box)로 embed 하여 answer node가 그 box 안에 위치하도록 한다.
•
Path query
◦
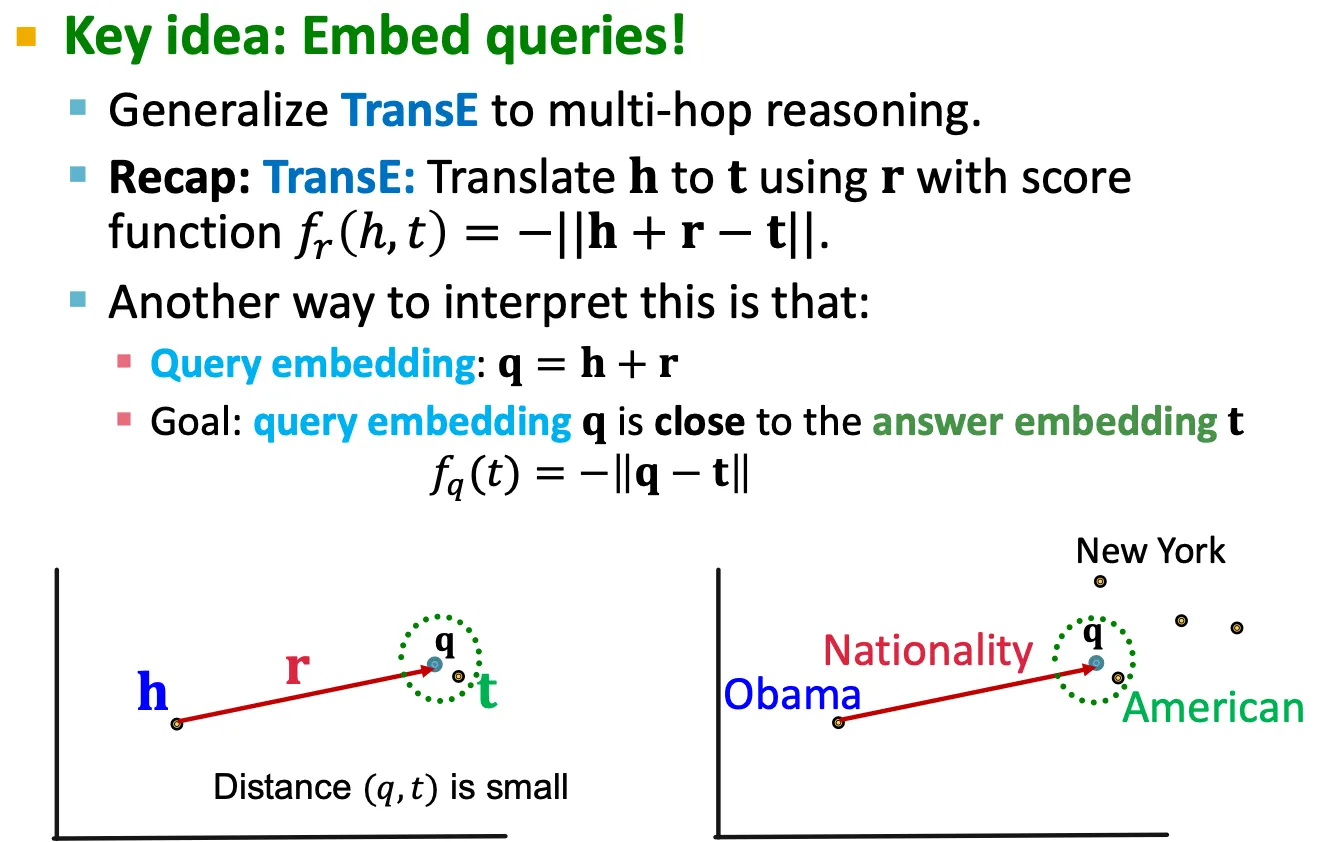
10강에서 배웠던 TransE를 적용할 수 있다.
▪
Query: q=h+r\mathbf{q} = \mathbf{h} + \mathbf{r}
▪
Answer embedding: t\mathbf{t}
◦
Path query는 그저 relation에 따라서 vector addition을 해주면 되므로, scalable하게 적용할 수 있다.
◦
단, TransR, DistMult, ComplEx 등은 compositional relation을 다루기 어려우므로, path query를 embed 할 때 적용하기는 어렵다.

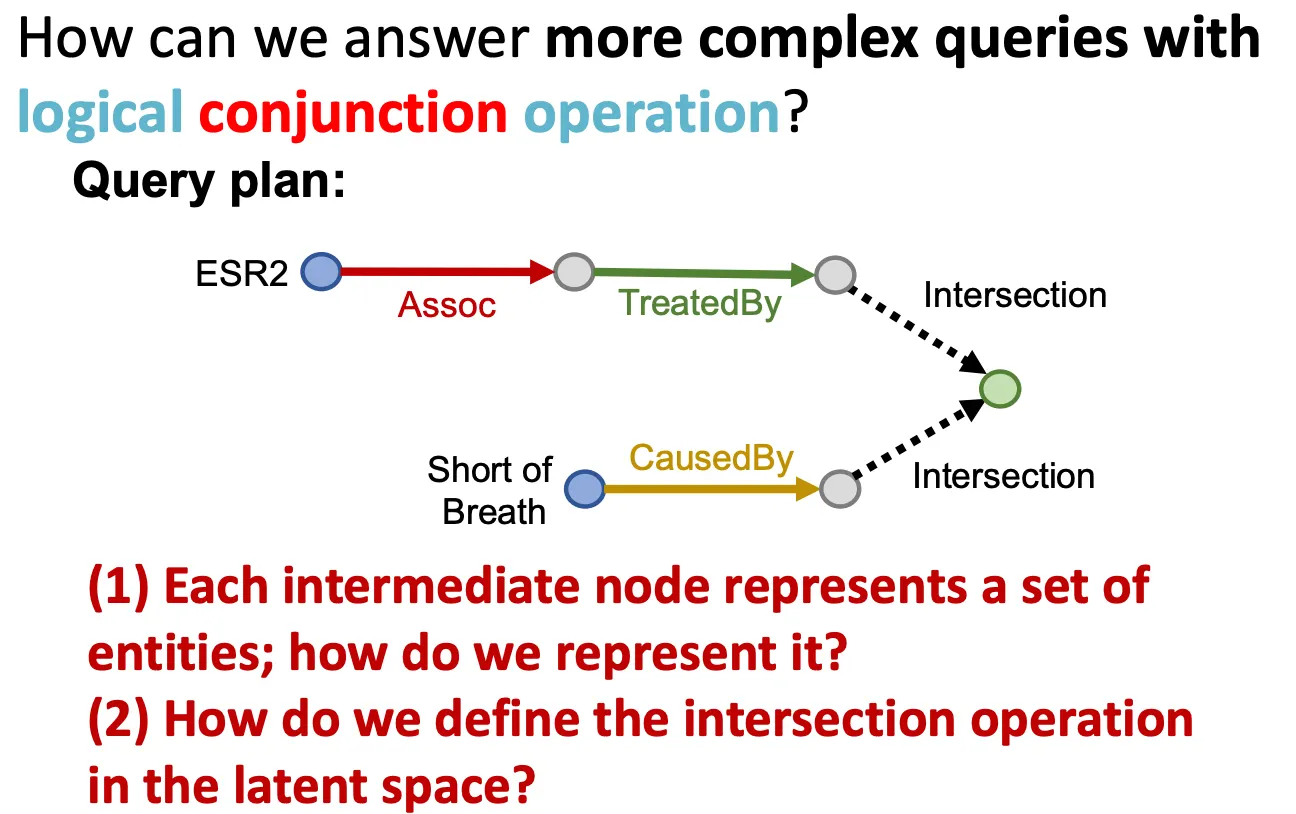
Conjunctive Queries (AND)

•
Logic conjunction operation (AND)가 포함된 더 복잡한 query는 어떻게 대답할 수 있는가?
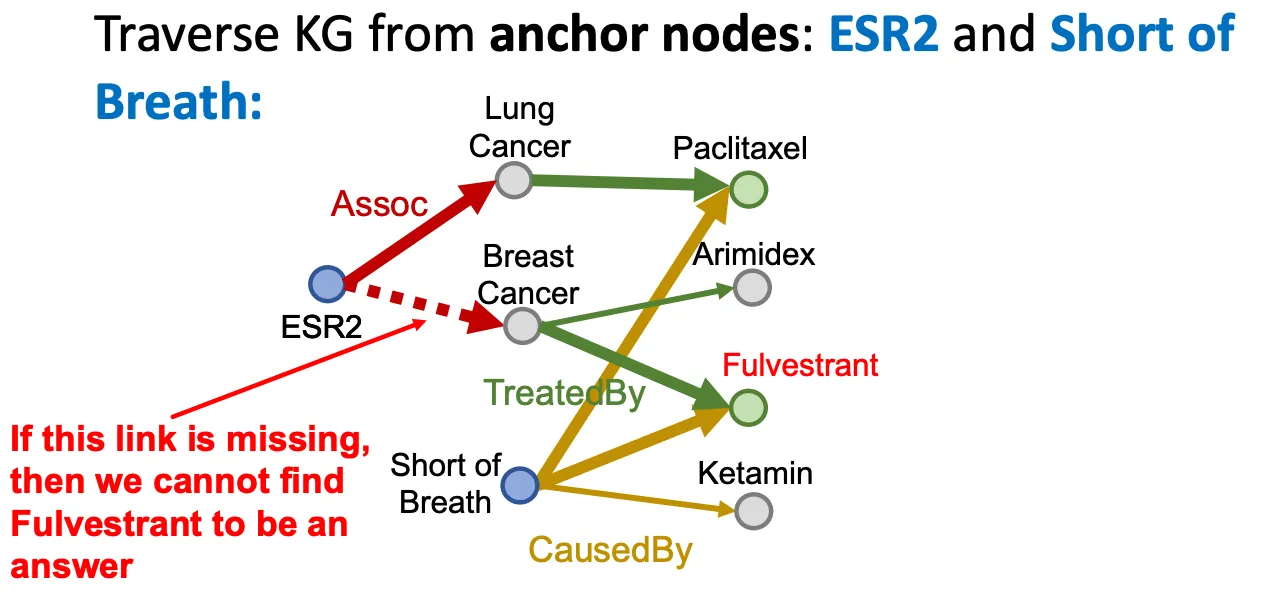
Traversing KG
•
Conjunctive query 역시 KG를 traversing 해서도 알 수도 있다.
•
하지만 incompleteness로 인해 어떤 link가 missing 되었다면, 제대로 답을 얻을 수 없는 상황이 쉽게 발생한다.
◦
이를 극복하기 위해서는 implicit하게 (ESR2,Assoc,BreastCancer)(ESR2, Assoc, Breast Cancer) 관계를 impute 해야한다.
◦
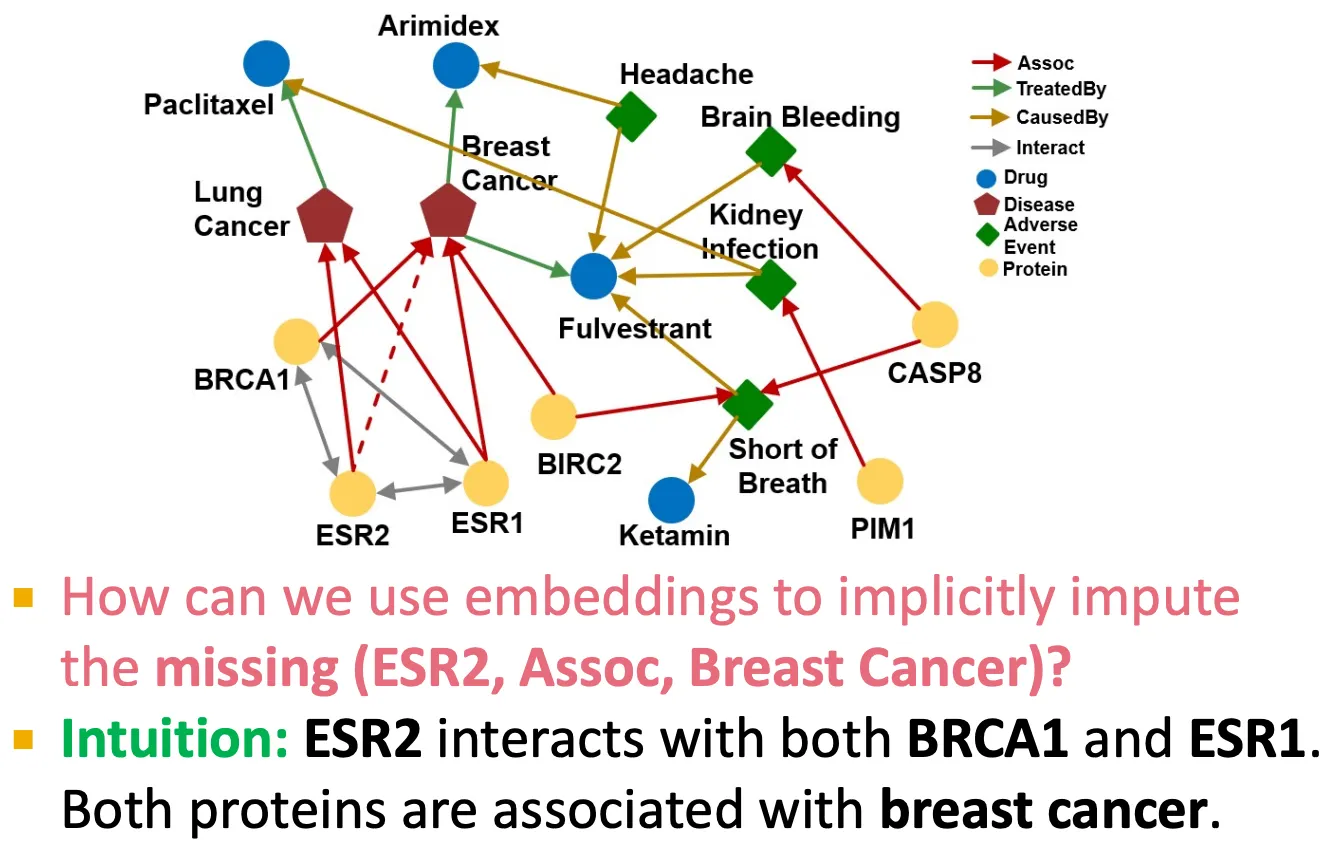
KG를 살펴보면, edge 하나가 missing 하더라도 주변 node들을 살펴보면 유추해서 사용할 수 있는 경우들이 있다.
ESR2가 BRCA1, ESR1과 상호작용하고, 그 두 protein 들은 breast cancer와 연관이 있으므로, 이 정보를 활용해볼 수 있을까?
◦
중간 node 들은 어떤 set으로 표현될 수 있는데, 이를 어떻게 잘 표현할 수 있을까? 또, intersection operation은 latent space에서 어떻게 잘 정의할 수 있을까?

Query2box: Reasoning over KGs using Box Embeddings

•
Box embeddings
◦
Query2box는 각 query를 hyper-rectangle 형태로 embedding 하는 것으로부터 출발한다.
e.g.) Fulvestrant의 adverse effect 를 하나의 box 안에 담기게 할 수 있다.
•
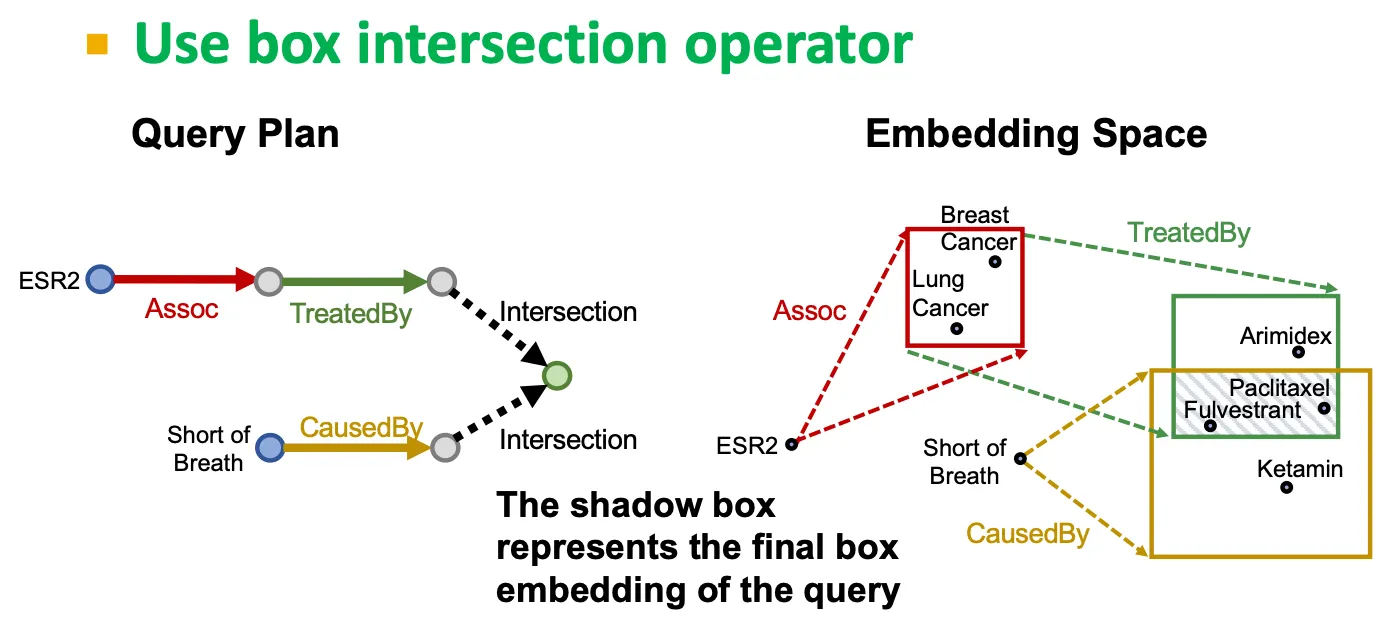
Intersection
Box의 intersection은 잘 정의되어 있듯이, 그냥 겹치는 부분을 의미한다.
•
Embed with box embedding
◦
Entity embeddings (# params: d∣V∣d |V|)
Entity는 zero-volume box.
◦
Relation embeddings (# params: 2d∣R∣2d|R|)
각 relation task는 box를 받고, 새로운 box를 생성한다.
◦
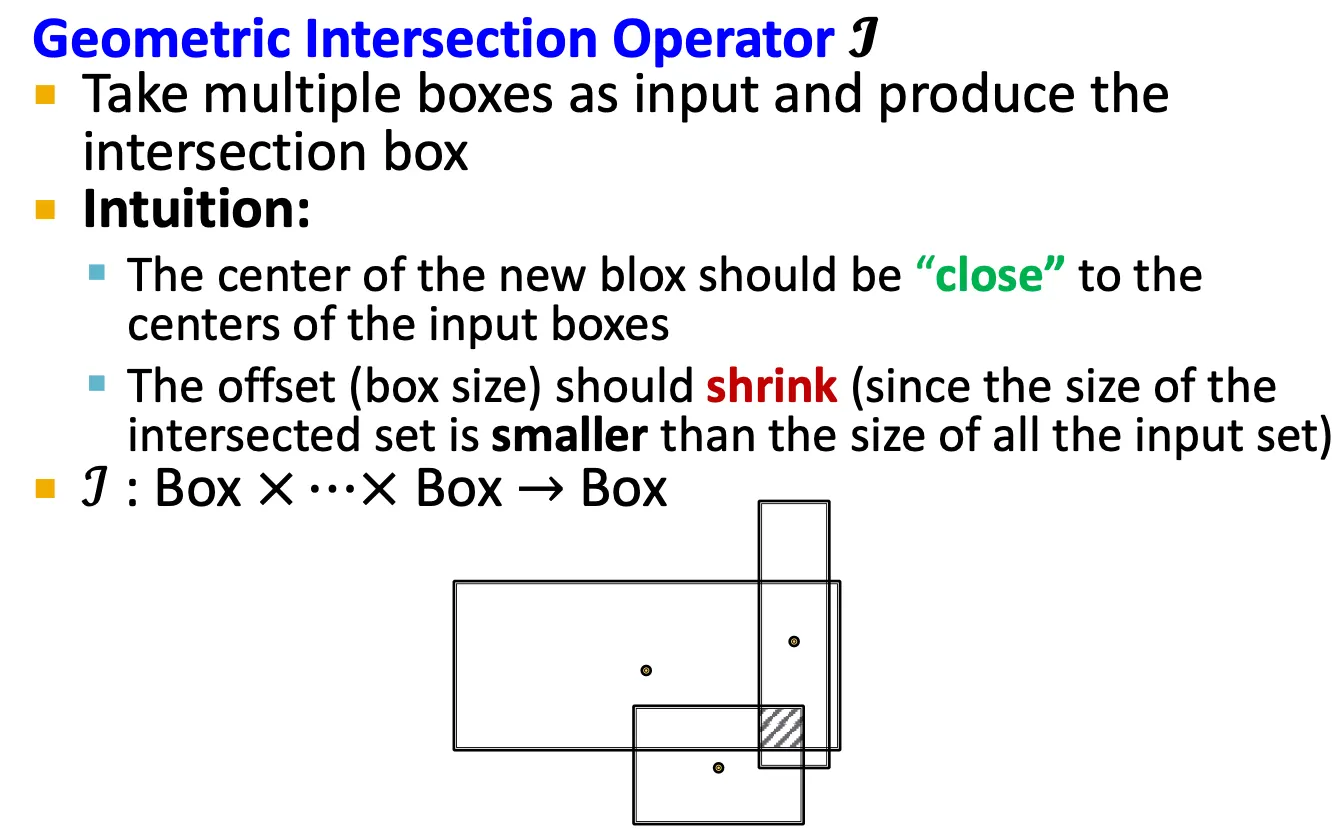
Intersection operator ff
새로운 operator로, box들을 받고, 다른 box를 output으로 뱉는다.
Box의 intersection을 modeling 한다.
◦
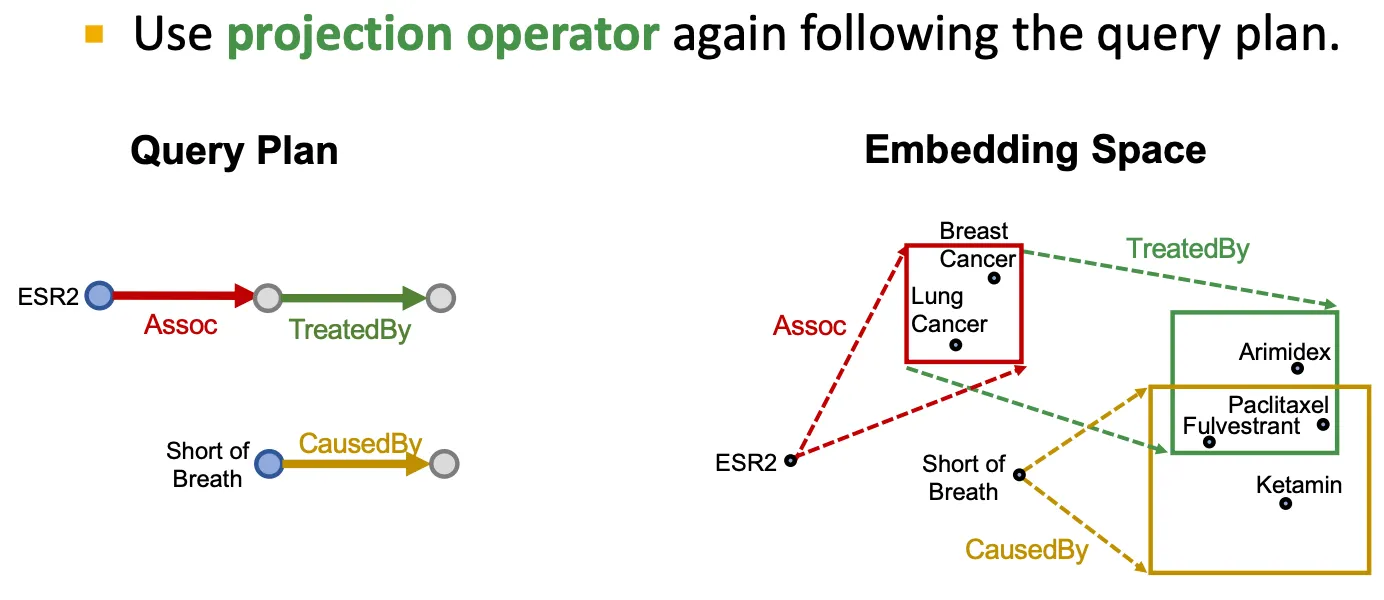
Projection operator
▪
어떤 box를 input으로 받아, relation embedding을 사용해 projection & expansion을 수행한다.
▪
그런데 box 끼리의 intersection은 어떻게 정의할까?
◦
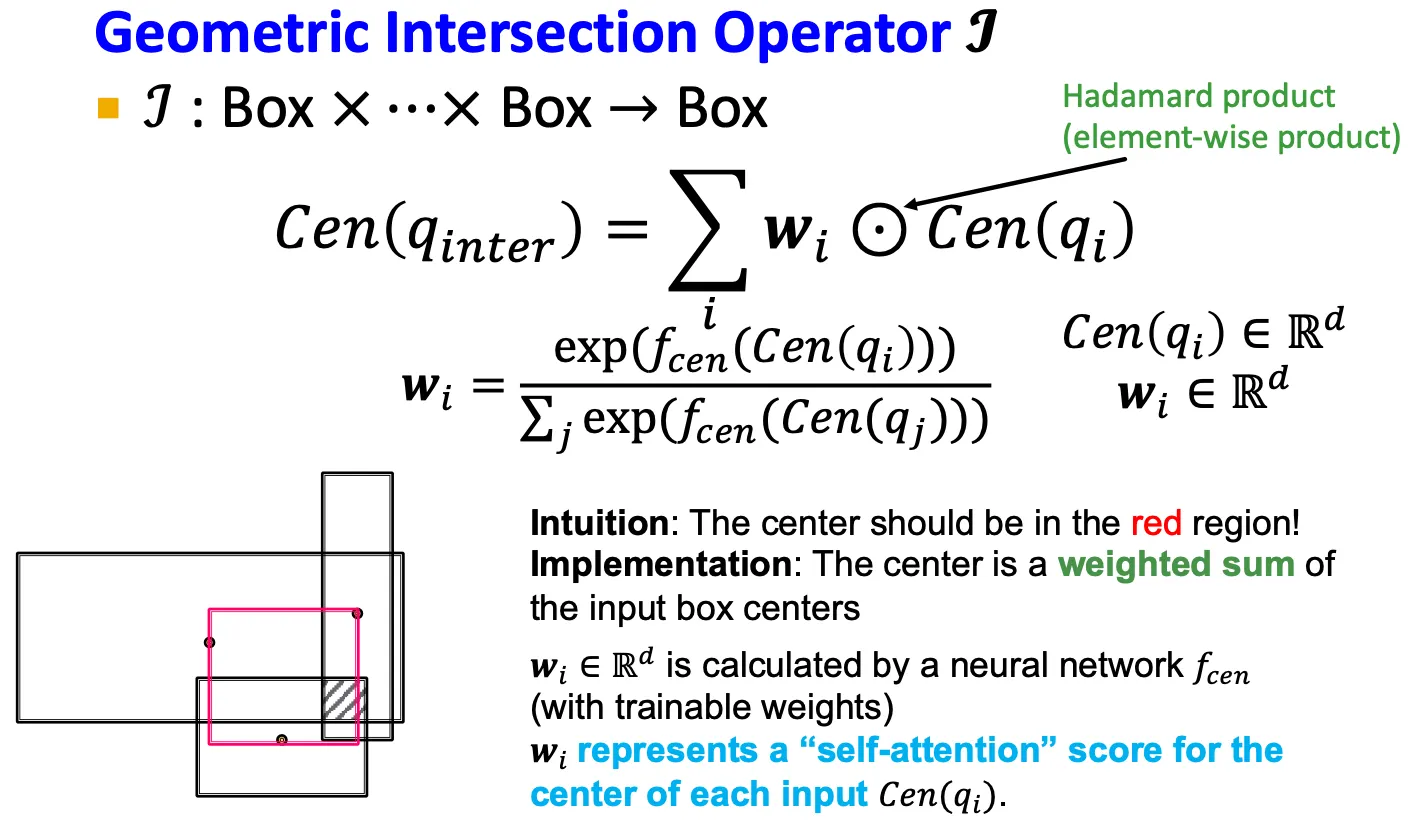
Intersection operator
Center
▪
fcenf_{cen}: neural network
▪
wiw_i: fcenf_{cen}으로부터 계산된 weight
▪
각 input으로부터 weight를 계산하고, input box들의 center들을 weighted sum을 하여 intersection의 center를 정의한다.
Offset (일종의 volume)
▪
fofff_{off}: neural network
▪
각 input box들의 offset에서 min을 취하고, 거기에 sigmoid (0~1 사이 값을 output으로 내놓는)를 적절히 취해 shrinking을 보장해준다.
•
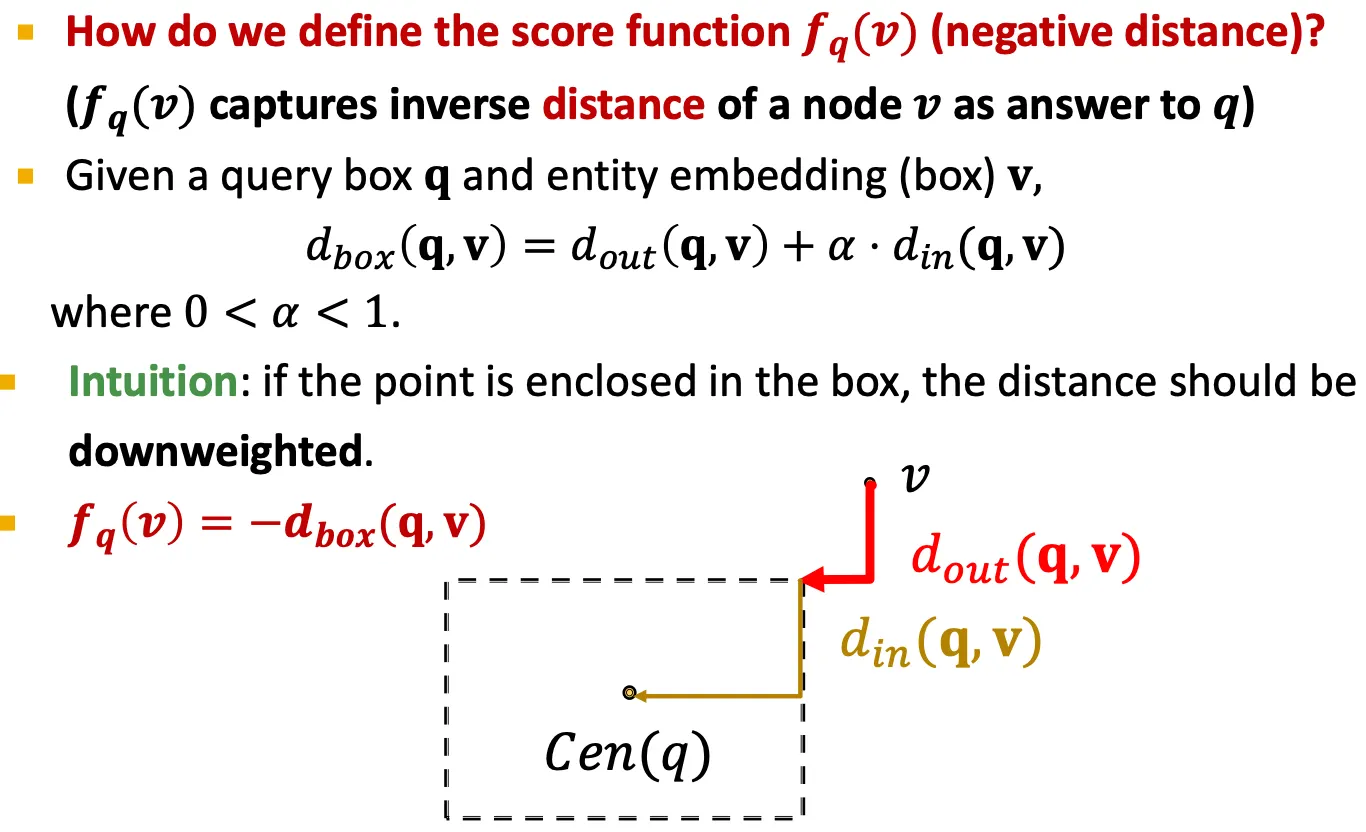
Entity-to-Box distance
Negative distance (negative sample의 score)도 계산해야 하는데 어떤 score function을 사용할 수 있을까?
◦
Out-distance (doutd_{out})과 in-distance (dind_{in}) 과의 weighted sum 이다.
◦
이때, out-distance에 더 penalize 해준다.
Extending to Union Operation
•
Union (OR)에도 적용할 수 있을까? 그리고 AND-OR query (AND와 OR가 섞인 query) 들을 low-dimensional vector space에 embedding 할 수 있을까?
불가능하다. 어떤 임의의 query에 대해 union을 허용하려면 high-dimensional embedding이 필요하다.
◦
어떤 MM개의 conjunctive query와 non-overlapping answer 들에 대해 우리는 모든 OR query들을 다루기 위해서는 최소 Θ(M)\Theta(M) 의 dimension 이 필요하다.
e.g.)
•
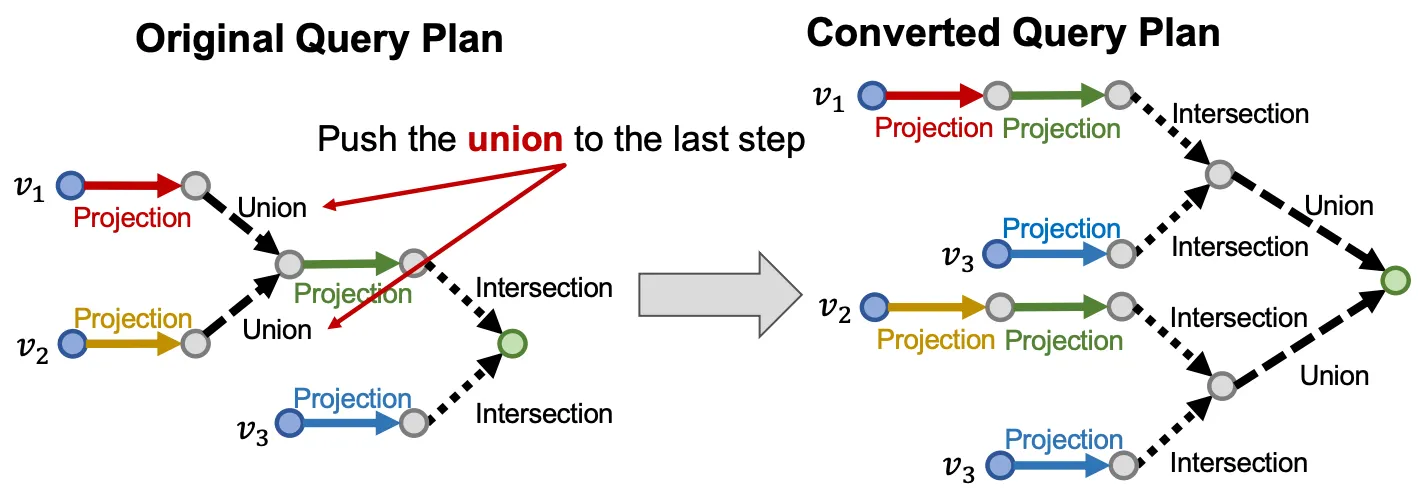
Low dimension에 embedding 할 수 없지만, handle은 가능한가?
Key idea: 중간에 위치한 union 을 모두 없애고 마지막을 union으로 바꾸자.
◦
Disjunctive normal form
모든 AND-OR query는 동치인 DNF 형태로 만들 수 있다.
q=q1∨q2∨...∨qmq = q_1 \vee q_2 \vee ... \vee q_m
▪
qq: AND-OR query
▪
qiq_i: conjunctive query
먼저 모든 qiq_i를 embedding 하고, 마지막 step에서 aggregate 하자.
이때, qq와 entity간의 거리는 아래의 식으로 정의한다.
dbox(q,v)=min⁡(dbox(q1,v),...,dbox(qm,v))d_{box}(\mathbf{q}, \mathbf{v}) = \min (d_{box}(\mathbf{q}_1, \mathbf{v}), ..., d_{box}(\mathbf{q}_m, \mathbf{v}))

How to Train Query2box

•
Key concepts
◦
Query와 그 answer, 그리고 negative answer를 KG로부터 어떻게 얻어낼 것인가?
◦
KG를 어떻게 잘 split 할 것인가?
Training
1.
Training graph GtrainG_{train}으로부터 query를 randomly sample 하고, answer와 negative answer도 sampling 한다.
2.
Query q\mathbf{q}를 embed 한다.
3.
Score fq(v)f_q(v)와 fq(v′)f_q(v')를 계산한다.
4.
fq(v)f_q(v)를 maximize 하고, fq(v′)f_q(v')를 minimize 한다.
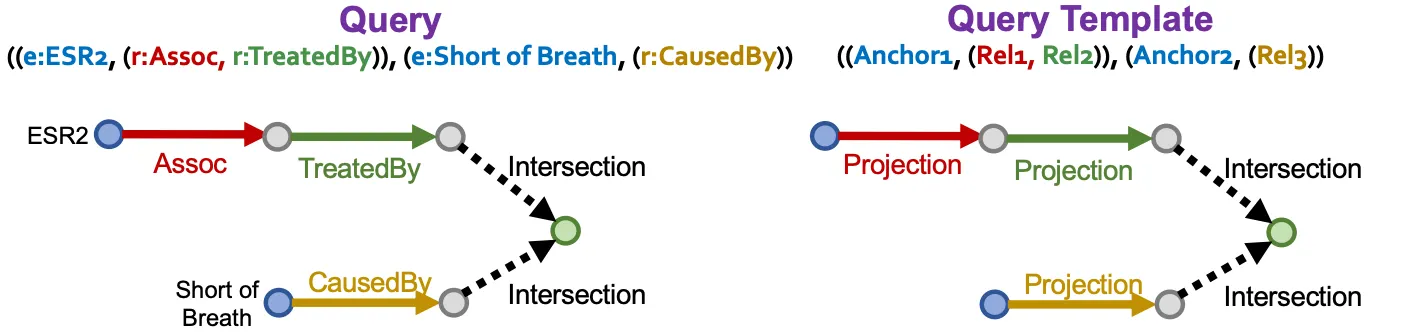
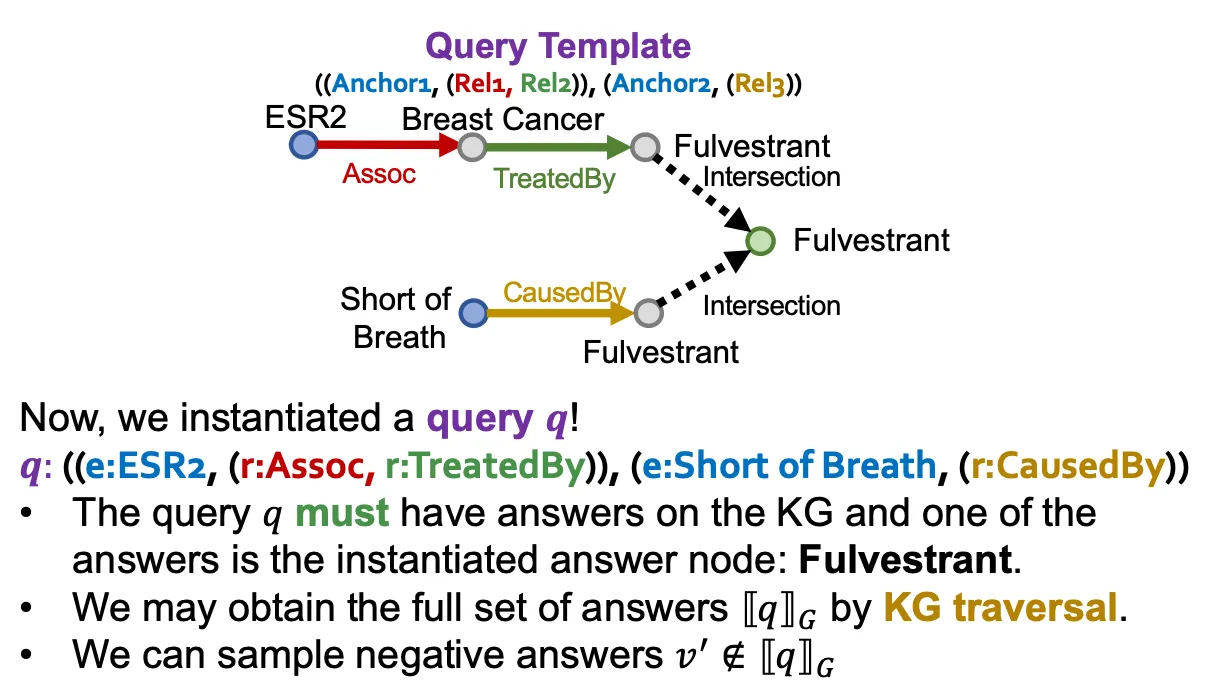
l=−log⁡(σ(fq(v))−log⁡(1−σ(fq(v′))\mathcal{l} = - \log (\sigma(f_q(v)) - \log (1-\sigma(f_q(v'))
Query generation from templates
•
Query template (entity type, relation type으로 정의)을 정해 query sample들을 만들어낸다.
◦
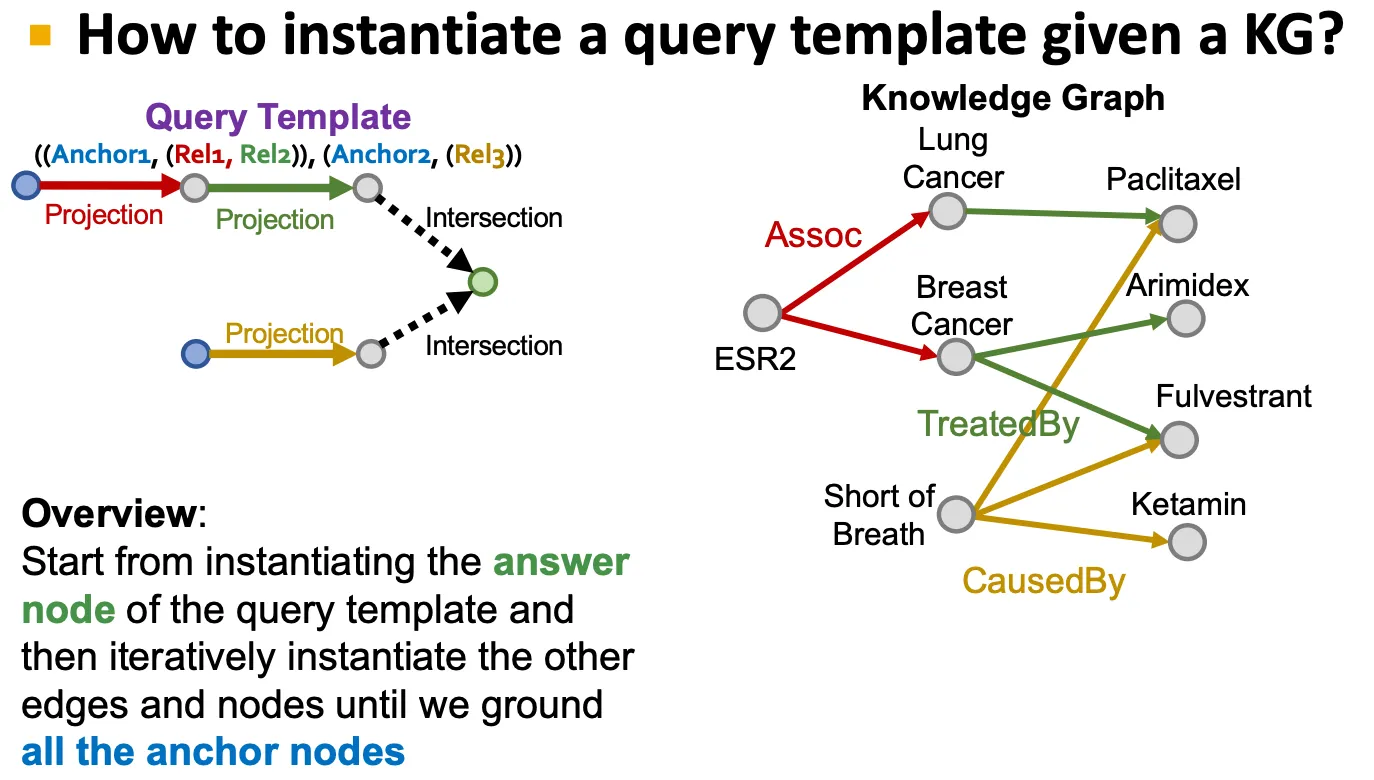
Query template의 answer node부터 시작해서 anchor node에 도달할 때까지 각 node 들을 instantiate 해나간다.
◦
KG에 존재하는 path들을 따라가서 (traversal 해서) answer를 만들고, entity, relation type만 동일하고 실제 traversal에서 없었던 negative answer를 만든다.