Search

[CS224W] Lecture 7

Recap: Deep Graph Encoders, GNNs

•
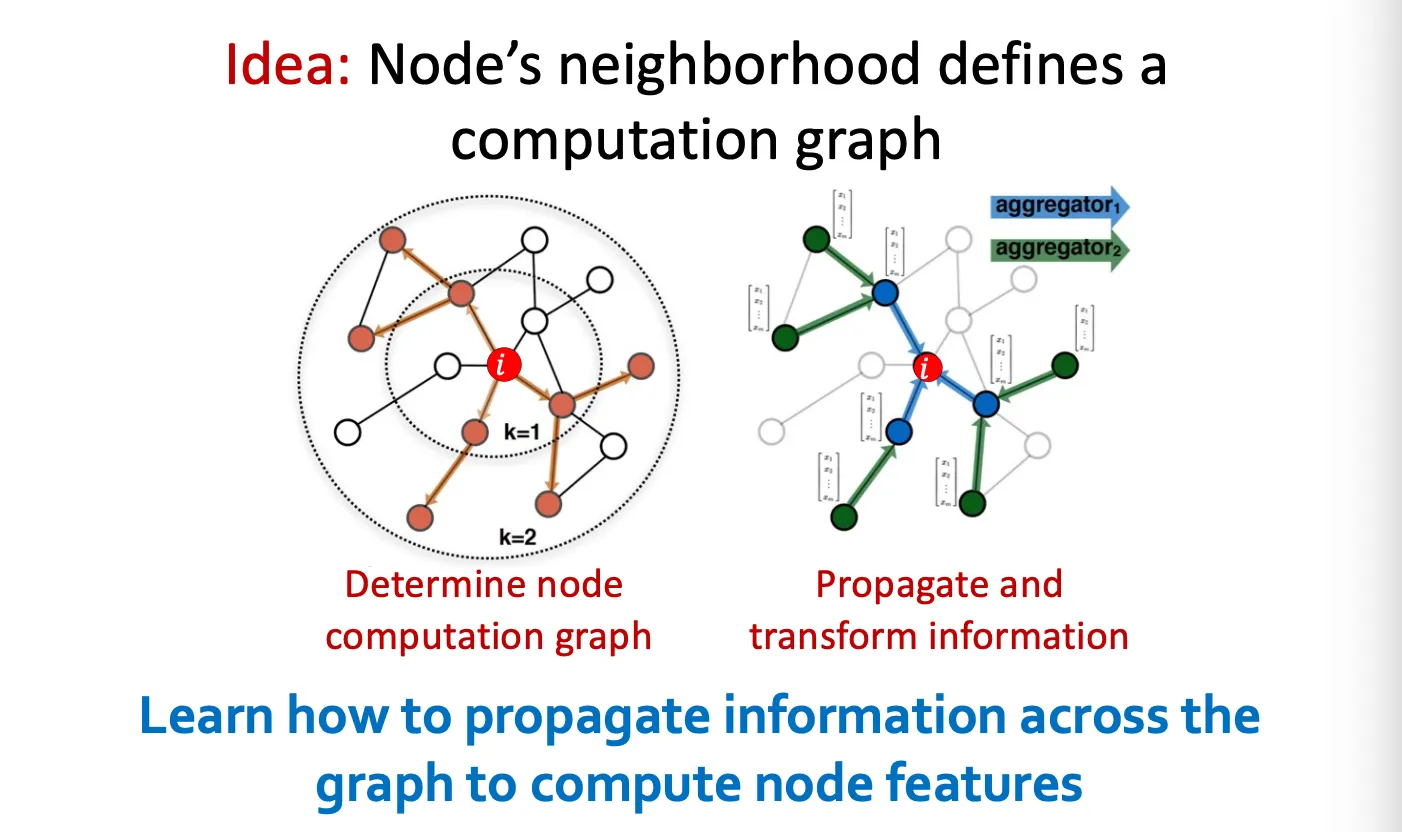
Aggregate Neighbors
Network에서 이웃과 일종의 computation graph가 형성되어 이웃의 정보를 aggregation 한다.
•
Why GNNs generalize other NNs?
GNN은 permutation invariance, equivariance의 개념이 적용된 형태로, CNN과 Transformer의 일반화된 형태로 볼 수 있다.
◦
CNN
Neighbor size가 고정되고 order가 정해진 GNN 형태이다.
◦
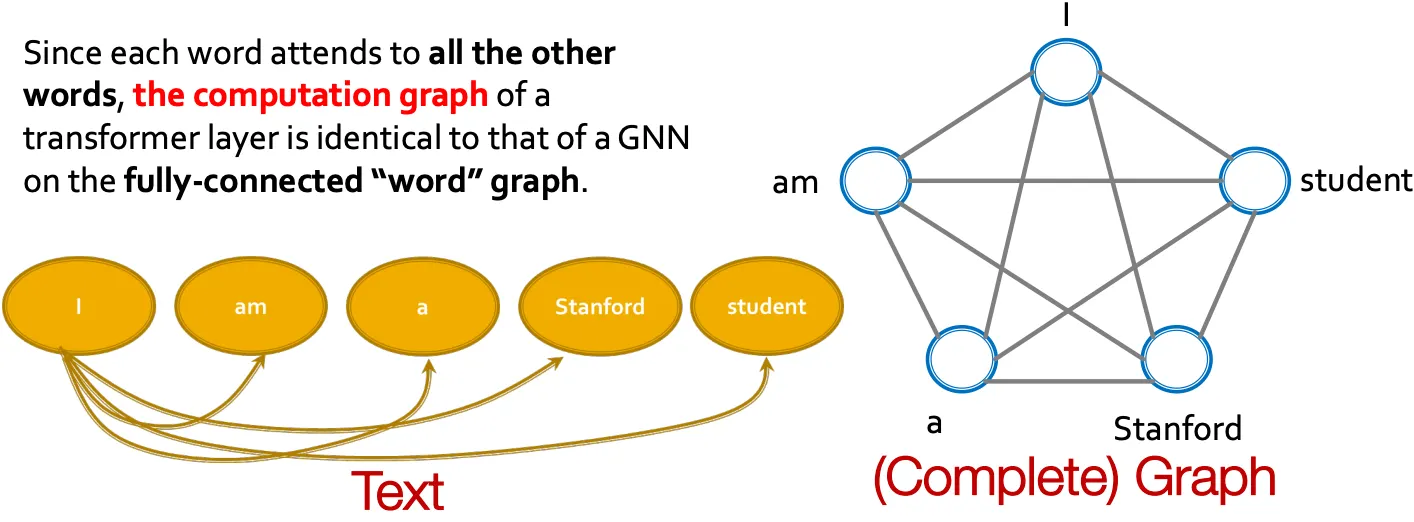
Transformer
Fully-connected word graph라고 생각하면 transformer도 GNN의 일종이다.

A General Perspective on GNNs

•
GNN Framework
1.
GNN layer: Message
2.
GNN layer: Aggregation
e.g.) GCN, GraphSAGE, GAT, …
3.
Stacking layers
여러 layer를 이어 쌓고, skip connection을 넣는 방법
4.
Graph augmentation
•
Graph feature augmentation
•
Graph structure augmentation
5.
Learning objective
•
Supervised/Unsupervised
•
Node/Edge/Graph

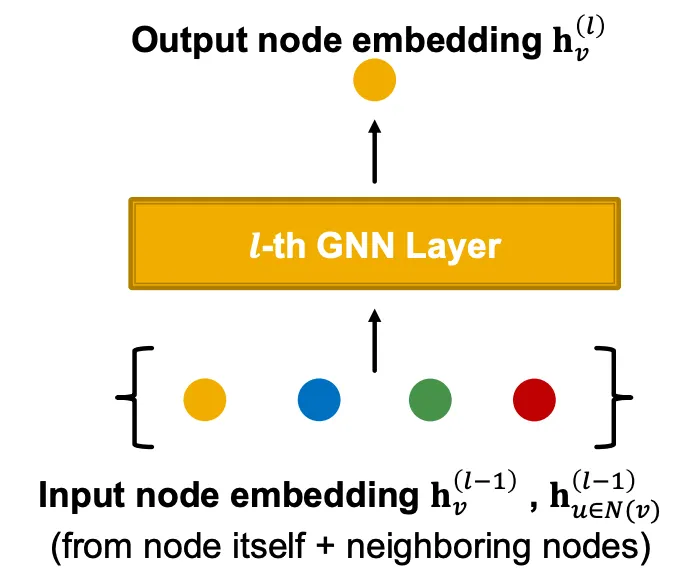
A Single Layer of a GNN

•
GNN layer
Idea: Vector의 집합을 하나의 vector로 압축하는 것!
Two-step process:
1.
Message
mu(l)=MSG(l)(hu(l−1))\mathbf{m}^{(l)}_u = \text{MSG}^{(l)} (\mathbf{h}^{(l-1)}_u)
각 node가 message를 만들고, 그 message가 나중에 다른 node 들로 전파된다.
Message functions
•
Linear layer 통과
mu(l)=W(l)hu(l−1)\mathbf{m}^{(l)}_u = \mathbf{W}^{(l)} \mathbf{h}^{(l-1)}_u
2.
Aggregation
hv(l)=AGG(l)({mu(l),u∈N(v)})\mathbf{h}^{(l)}_v = \text{AGG}^{(l)}(\{ \mathbf{m}^{(l)}_u, u \in N(v)\})
각 node가 주변 이웃 node들의 message를 aggregate 한다.
Aggregation은 order invariant 해야한다.
Aggregation functions
•
Sum/Mean/Max
hv(l)=Sum({mu(l),u∈N(v)})\mathbf{h}^{(l)}_v = \text{Sum}(\{ \mathbf{m}^{(l)}_u, u \in N(v)\})
•
Message Aggregation: Issue & Solution
Issue: 이웃 node 들의 정보만 aggregate 하면 node vv 자신의 정보가 없어질 수 있다.
Solution: hv(l)\mathbf{h}^{(l)}_v를 계산할 때 hv(l−1)\mathbf{h}^{(l-1)}_v도 사용한다.
1.
Message
mu(l)=Whu(l−1)\textcolor{blue}{\mathbf{m}^{(l)}_u} = \mathbf{W}\mathbf{h}^{(l-1)}_u, mv(l)=B(l)hv(l−1)\textcolor{red}{\mathbf{m}^{(l)}_v }= \mathbf{B}^{(l)}\mathbf{h}^{(l-1)}_v
보통 message computation은 neighbor와 self가 다른 weight parameter를 사용해 계산된다.
2.
Aggregation
hv(l)=CONCAT(AGG({mu(l),u∈N(v)}),mv(l))\mathbf{h}^{(l)}_v = \text{CONCAT}(\text{AGG}(\{\textcolor{blue}{\mathbf{m}^{(l)}_u}, u \in N(v)\}), \textcolor{red}{\mathbf{m}^{(l)}_v})
Neighbor로부터 aggregate할 때 자신의 정보를 사용해서 concat 또는 sum 한다.
•
Putting this together
1.
Message
mu(l)=MSG(l)(hu(l−1)),u∈{N(v)∪v}\mathbf{m}^{(l)}_u = \text{MSG}^{(l)} (\mathbf{h}^{(l-1)}_u), u \in \{N(v) \cup v\}
2.
Aggregation
hv(l)=AGG({mu(l),u∈N(v)},mv(l))\mathbf{h}^{(l)}_v = \text{AGG}(\{\mathbf{m}^{(l)}_u, u \in N(v)\}, {\mathbf{m}^{(l)}_v})
3.
Non-linearity
Expressiveness를 위해 ReLU, Sigmoid 등을 사용한다.
Message 또는 aggregation에 사용할 수 있다.
•
Classical GNN Layers
◦
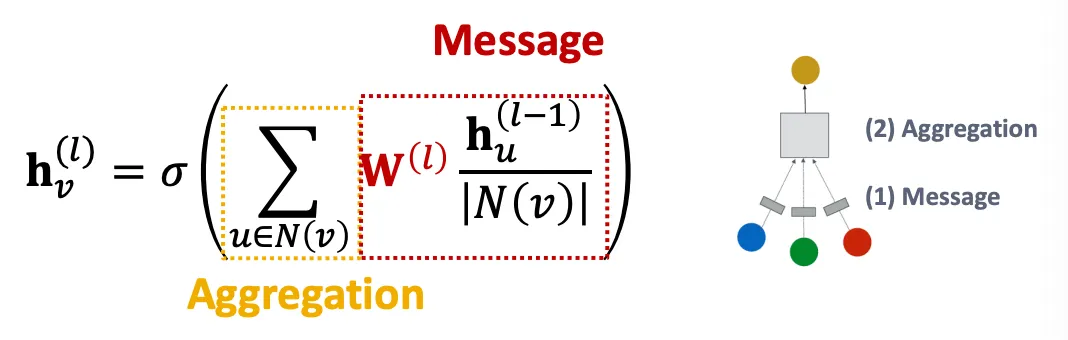
Graph Convolutional Networks (GCN)
hv(l)=σ(∑u∈N(v)W(l)hu(l−1)∣N(v)∣)\mathbf{h}^{(l)}_v = \sigma (\sum_{u \in N(v)} \mathbf{W}^{(l)}\frac{\mathbf{h}^{(l-1)}_u}{|N(v)|})
1.
Message
mu(l)=1∣N(v)∣W(l)hu(l)\mathbf{m}^{(l)}_u = \frac{1}{|N(v)|} \mathbf{W}^{(l)}\mathbf{h}^{(l)}_u
Weight matrix를 곱한 뒤 node degree로 normalize를 하여 각 node의 embedding을 만든다.
2.
Aggregation
이웃 노드로부터 sum을 하고, activation을 적용한다.
표현은 Sum 이지만, node degree로 normalize 하므로 결국 average 이다.
hv(l)=σ(Sum({mu(l),u∈N(v)}))\mathbf{h}^{(l)}_v = \sigma (\text{Sum}(\{\mathbf{m}^{(l)}_u, u \in N(v) \}))
참고) GCN에서는 graph에 self-edge가 추가되어 있어, summation에 기본으로 포함된다.
◦
GraphSAGE
hv(l)=σ(W(l)⋅CONCAT(hv(l−1),AGG({hu(l−1),∀u∈N(v)})))\mathbf{h}^{(l)}_v = \sigma(\mathbf{W}^{(l)} \cdot \text{CONCAT}(\mathbf{h}^{(l-1)}_v, \text{AGG}(\{\mathbf{h}^{(l-1)}_u, \forall u \in N(v)\})))
Two-stage aggregation
▪
Stage 1: Node neighbor로부터 aggregation
hN(v)(l)←AGG({hu(l−1),∀u∈N(v)})\mathbf{h}^{(l)}_{N(v)} \leftarrow \text{AGG}(\{ \mathbf{h}^{(l-1)}_u, \forall u \in N(v)\})
▪
Stage 2: 이후 자기 자신으로부터도 aggregation
hv(l)←σ(W(l)⋅CONCAT(hv(l−1),hN(v)(l)))\mathbf{h}^{(l)}_v \leftarrow \sigma(\mathbf{W}^{(l)} \cdot \text{CONCAT}(\textcolor{red}{\mathbf{h}^{(l-1)}_v}, \mathbf{h}^{(l)}_{N(v)}))
Aggregation 하는 방법은 Mean, Pool, LSTM 등을 사용할 수 있다.
참고) LSTM은 order가 있는 language model이기 때문에 order를 계속 shuffle해서 사용한다.
L2 normalization
모든 layer에서 hv(l)←hv(l)∥hv(l)∥2\mathbf{h}^{(l)}_v \leftarrow \frac{\mathbf{h}^{(l)}_v}{\| \mathbf{h}^{(l)}_v\|_2}
Embedding vector를 L2 normalization으로 scaling 해준다.
◦
Graph Attention Networks (GAT)
hv(l)=σ(∑u∈N(v)αvuW(l)hu(l−1))\mathbf{h}^{(l)}_v = \sigma (\sum_{u \in N(v)} \alpha_{vu} \mathbf{W}^{(l)}\mathbf{h}^{(l-1)}_u)
▪
GCN, GraphSAGE에서는 aggregation 시에 모든 neighbor가 동일한 weight를 가져간다.
▪
하지만 GAT에서는 모든 node가 동일하게 중요하지는 않을 것이라는 intuition에 기반하여 attention을 적용한다.
▪
Attention mechanism
1.
Attention coefficient evue_{vu}가 아래와 같이 계산된다.
evu=a(W(l)hu(l−1),W(l)hv(l−1))e_{vu} = a (\mathbf{W}^{(l)}\mathbf{h}^{(l-1)}_u, \mathbf{W}^{(l)}\mathbf{h}^{(l-1)}_v)
evue_{vu}는 node vv의 입장에서, node uu의 중요도를 의미한다.
e.g.) attention의 형태 예시
•
eab=Linear(CONCAT(W(l)ha(l−1),W(l)hb(l−1)))e_{ab} = \text{Linear}(\text{CONCAT} (\mathbf{W}^{(l)}\mathbf{h}^{(l-1)}_a, \mathbf{W}^{(l)}\mathbf{h}^{(l-1)}_b)) ..?
2.
Normalize evue_{vu} → αvu\alpha_{vu}
αvu=exp⁡(evu)∑k∈N(v)exp⁡(evk)\alpha_{vu} = \frac{\exp(e_{vu})}{\sum_{k \in N(v)}\exp(e_{vk})}
3.
Weighted sum based on αvu\alpha_{vu}
hv(l)=σ(∑u∈N(v)αvuW(l)hu(l−1))\mathbf{h}^{(l)}_v = \sigma(\sum_{u \in N(v)}\alpha_{vu} \mathbf{W}^{(l)}\mathbf{h}^{(l-1)}_u)
▪
Form of attention mechanism
다양한 attention mechanism을 사용할 수 있다.
e.g.) Simple single-layer neural network
Attention mechanism의 parameter는 함께(jointly) 학습된다.
▪
Multi-head attention
일종의 ensemble 개념으로 attention process를 안정화해준다.

GNN Layers in Practice

•
Classic GNN layer를 먼저 사용해보는 것이 좋은 시작 지점이다.
•
다양한 현재 deep learning technique을 GNN layer에 도입할 수 있다.
◦
Batch normalization
한 batch에 해당하는 input들에 대해 mean 과 variance를 계산하여, zero mean, unit variance의 분포를 띄도록 scaling을 해주는 방법으로, 학습을 안정화시켜준다.
◦
Dropout
Overfitting을 방지하는 방법으로, training 시에는 일정 비율만큼의 node를 turn-off 하고, test 시에는 모두 사용하는 방법이다.
GNN에 적용할 때는 주로 message function의 linear layer에 적용한다.
◦
Activation
ReLU, Sigmoid, Parametric ReLU 등을 사용한다.

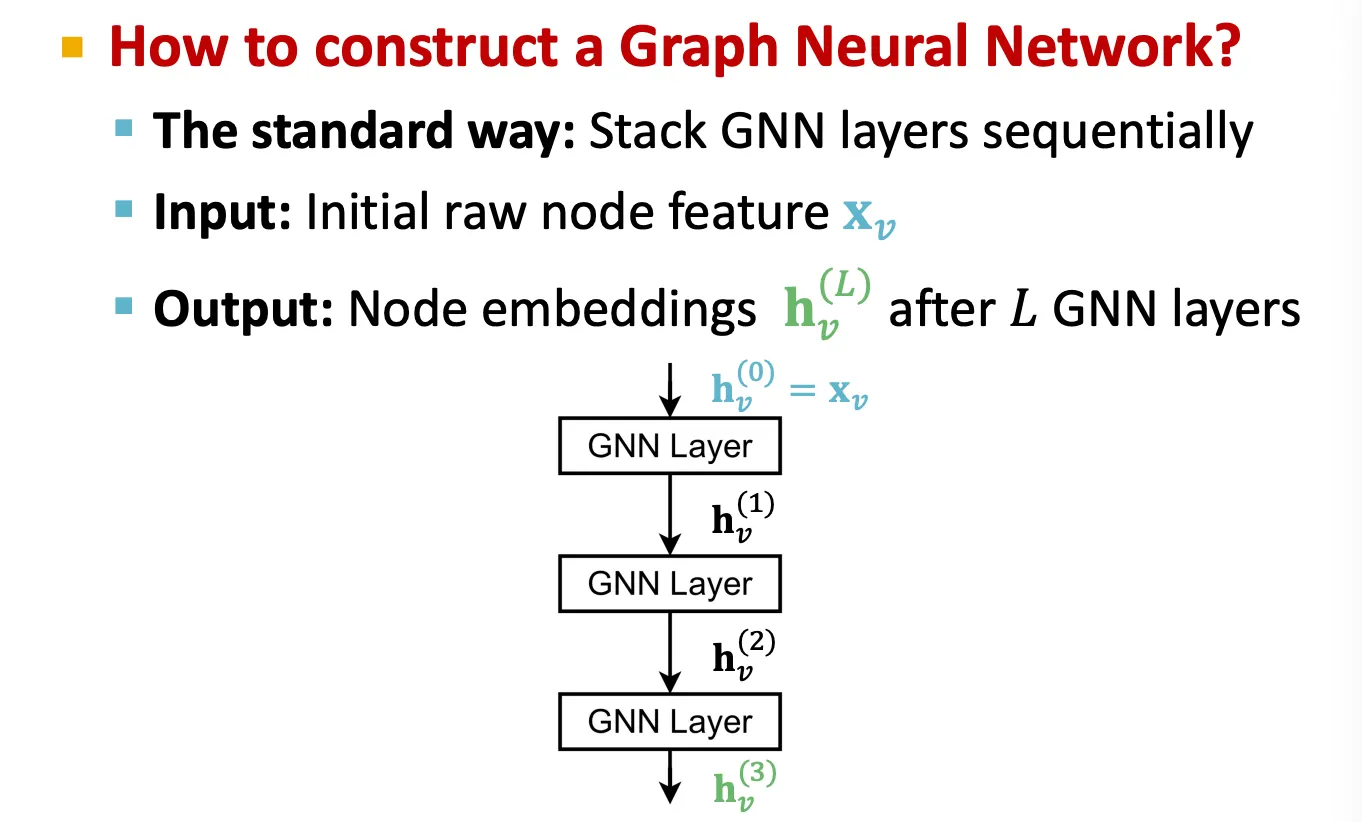
Stacking Layers of a GNN

일반적으로, GNN layer를 쌓을 때는 순차적으로 여러 층을 쌓는다.
•
Oversmoothing
하지만 naïve한 방법으로 여러 층을 쌓으면 over-smoothing problem이 발생하는데, 이는 모든 node의 embedding이 비슷한 값으로 수렴하여 node 들을 구분할 수 없는 수준에 도달하는 현상이다.
•
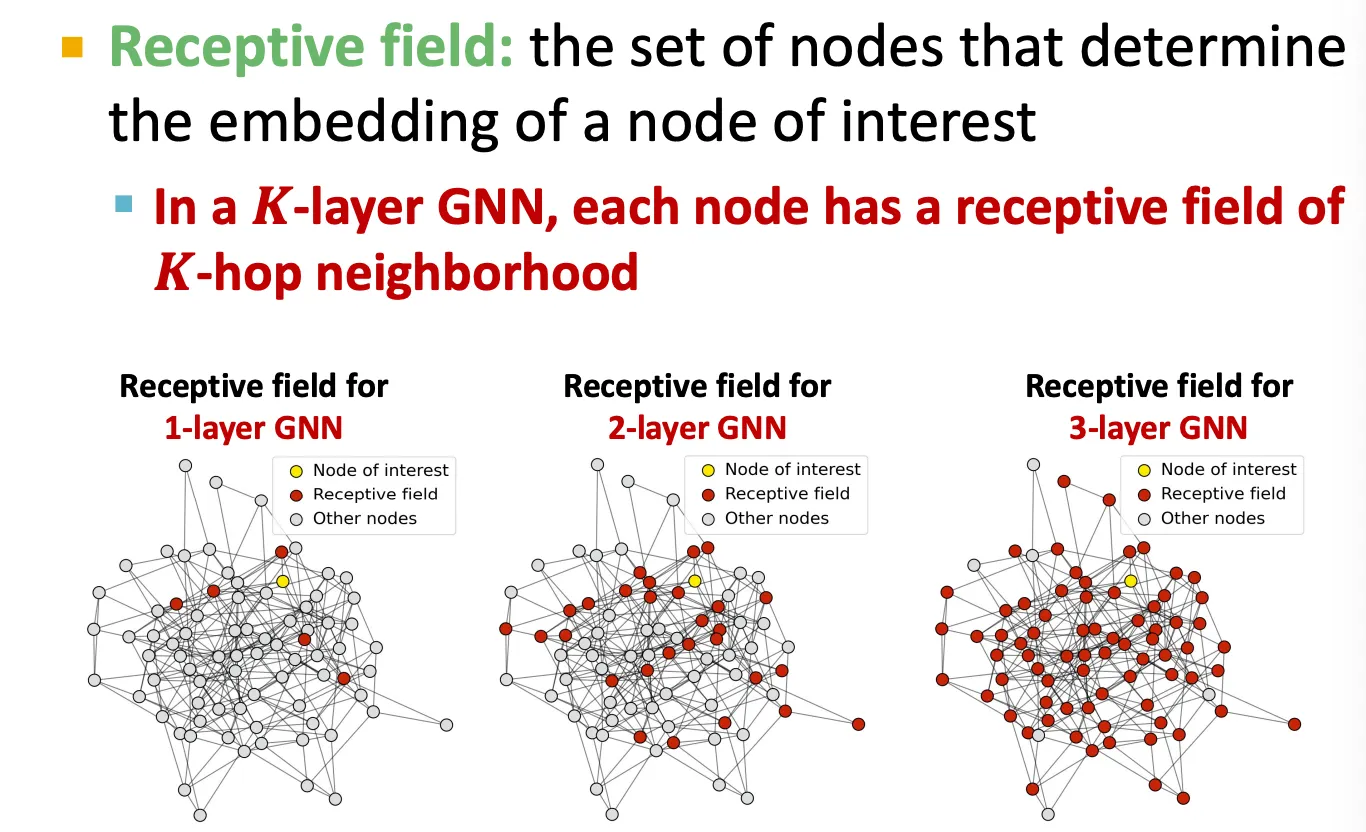
Receptive field of a GNN
CNN에서와 비슷하게, GNN도 receptive field 를 정의할 수 있는데, 어떤 node에 대해 얼마나 주변 node를 볼 것인지를 의미한다.
KK-layer GNN에서는 receptive field 가 KK-hop 만큼의 이웃들이다.
따라서 깊게 쌓을 수록 거의 대부분의 node들의 정보를 aggregate 하게 된다.
•
Oversmoothing 문제를 극복하는 방법
◦
Receptive field
GNN layer를 쌓을 때는 일반적인 neural network (MLP, CNN 등)를 쌓을 때처럼 층을 단순히 쌓으면 안 된다.
Domain에 맞게, receptive field가 얼마나 필요할지 분석해서 사용한다.
◦
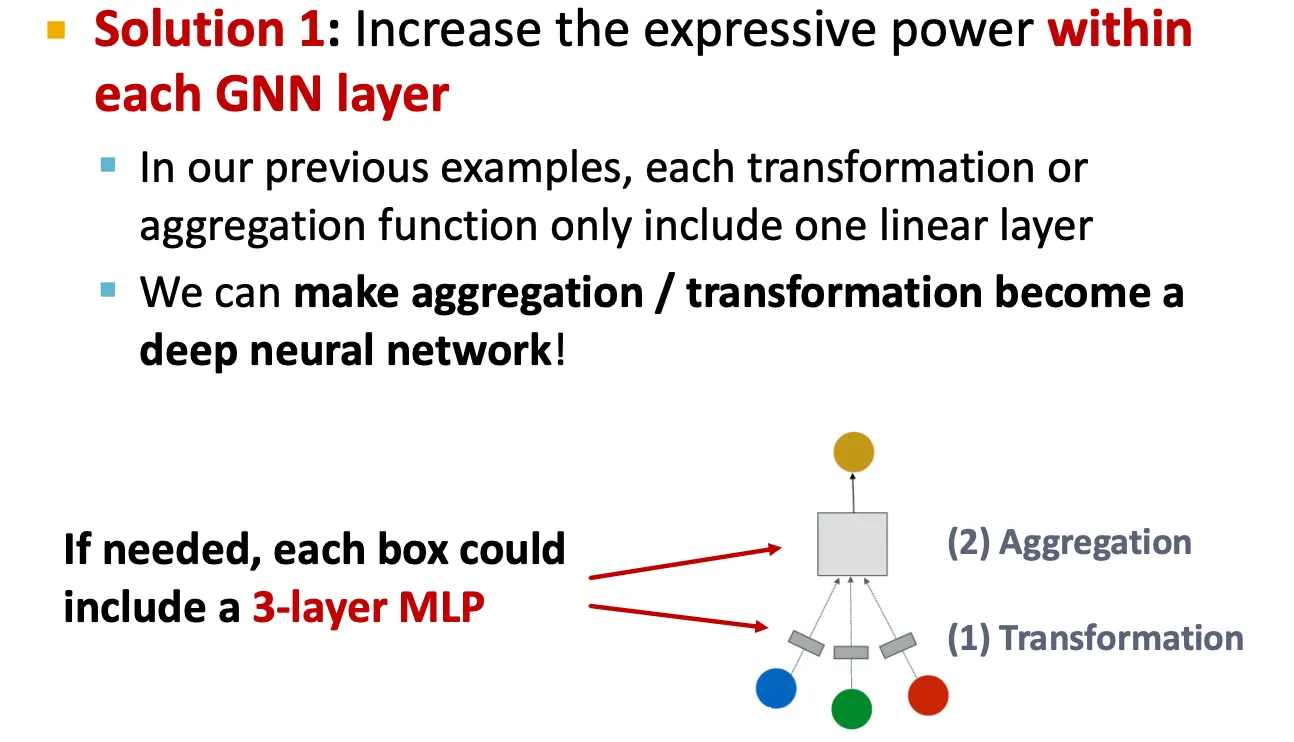
Expressive power
▪
GNN layer를 깊게 쌓지 말고, message function, aggregation function을 deep neural net으로 쌓아 expressivity를 높인다.
▪
GNN layer 사이에 pre-process, post-process layer를 쌓는다.
◦
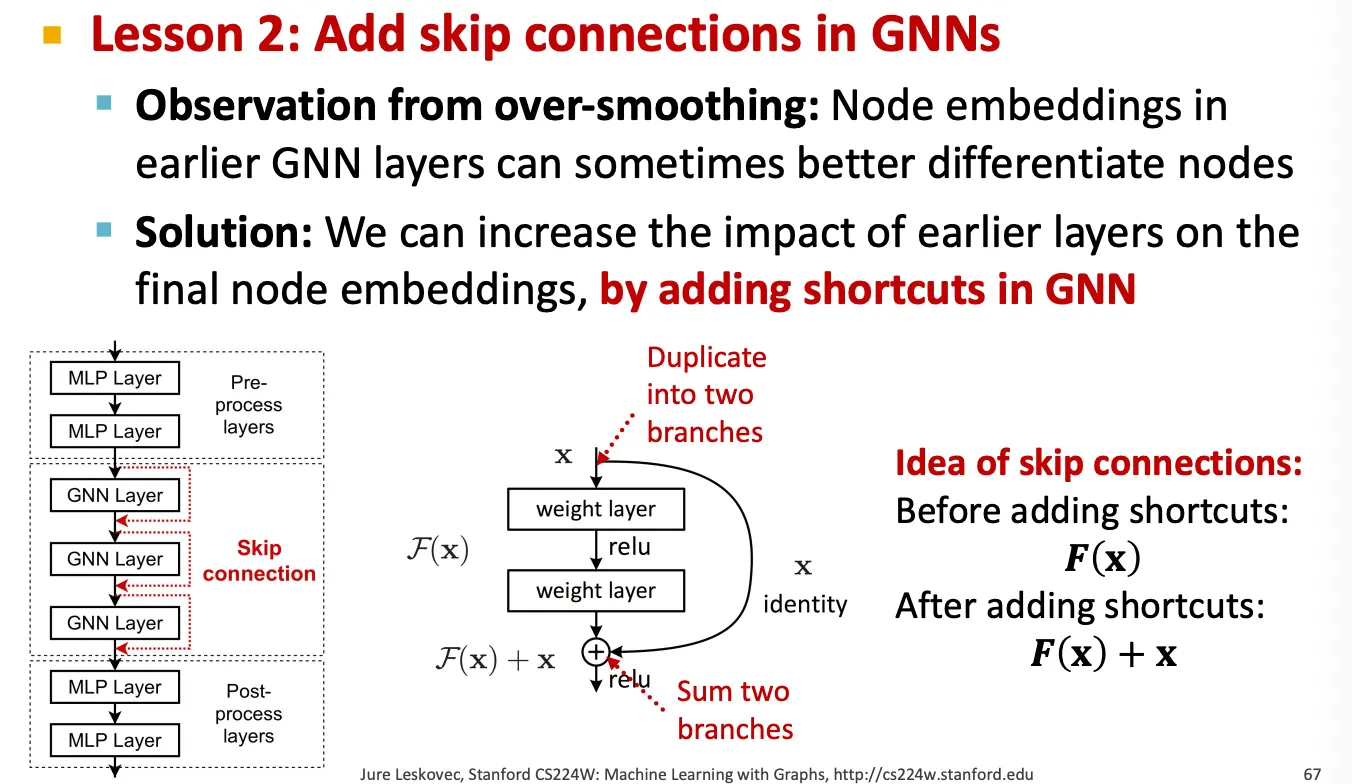
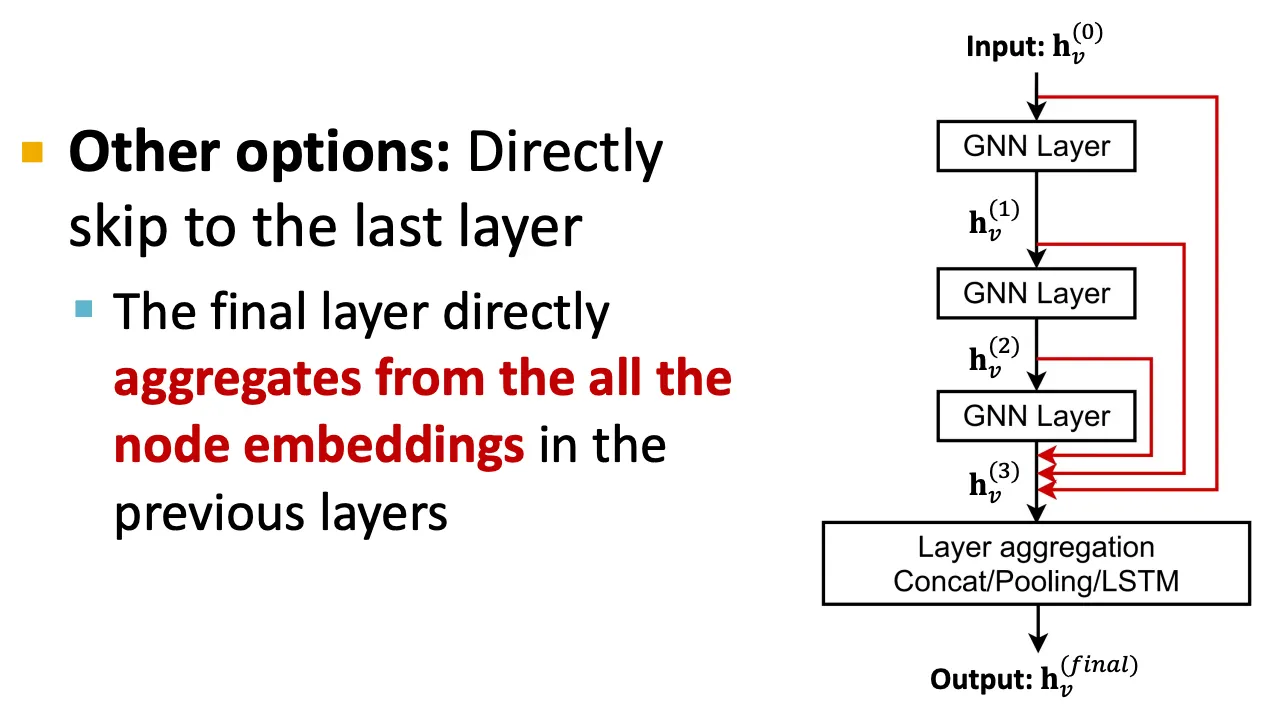
Skip-connection
만약 GNN layer를 어쩔 수 없이 깊게 쌓아야 할 경우에는 skip connection을 이용해 앞 layer에서 얻은 embedding을 직접 더해서 사용해준다.
이 방법은 model을 mixture 형태로 사용하는 효과가 있다.
▪
Skip connection을 수행하는 방법은 크게 2가지가 있다.
1.
Vanilla skip connection
h 가 밖에 있으면 안 되나..?
2.
Jumping knowledge (맞는지 확인 필요)