Table of Contents
•
Multi-task reinforcement learning problem
•
Policy gradients & their multi-task/meta counterparts
•
Q-learning
•
Multi-task Q-learning
Multi-task reinforcement learning problem
사실 많은 task가 sequential decision making이 필요하다. 그렇지 않은 것들의 예시는 단순한 classification, regression 등이 있다. 이외에 robotics, language, autonomous driving 등에서는 순차적인 결정이 최종 결과에 큰 영향을 미친다.
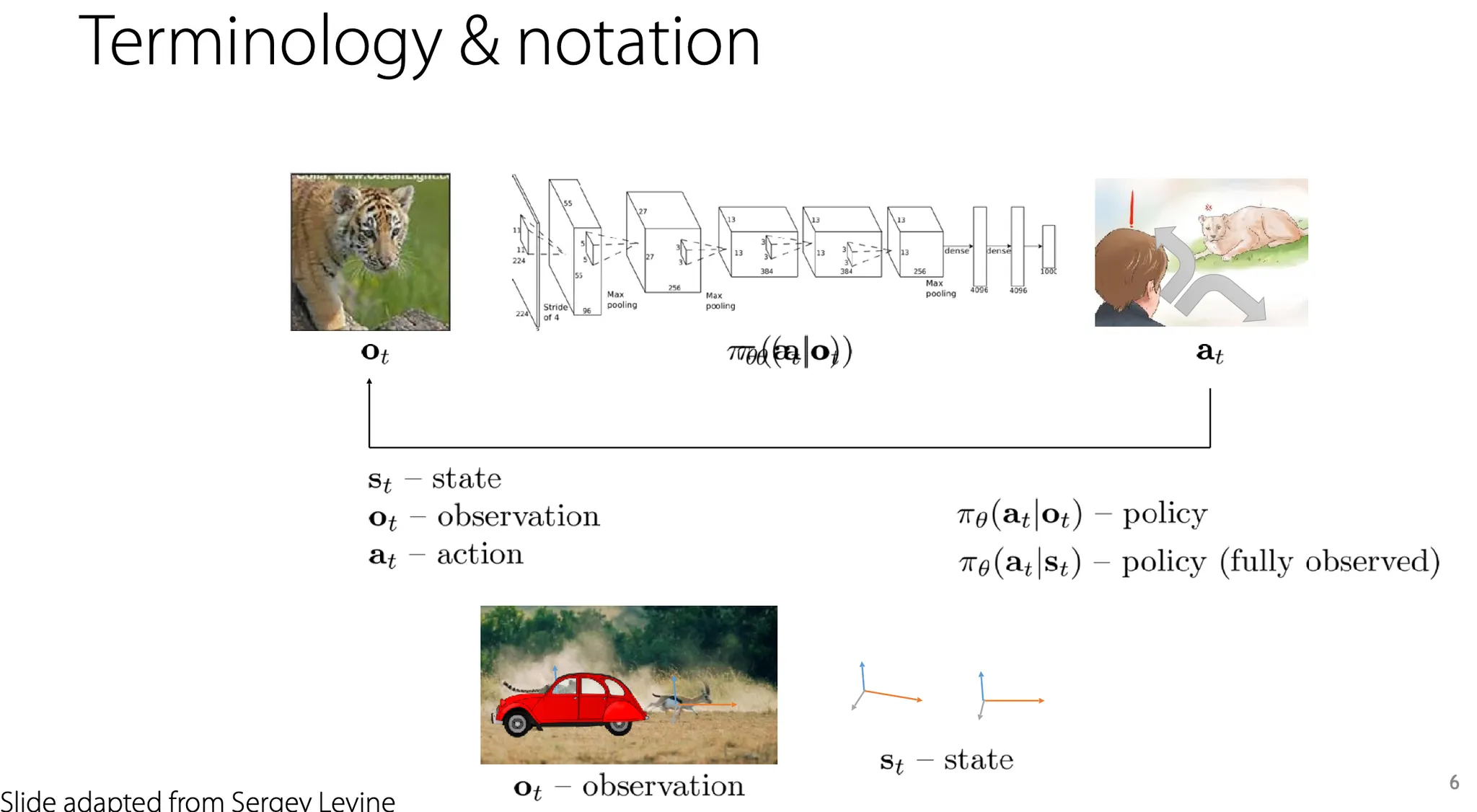
Object classification와 manipulation은 위와 같이 나눌 수 있다.
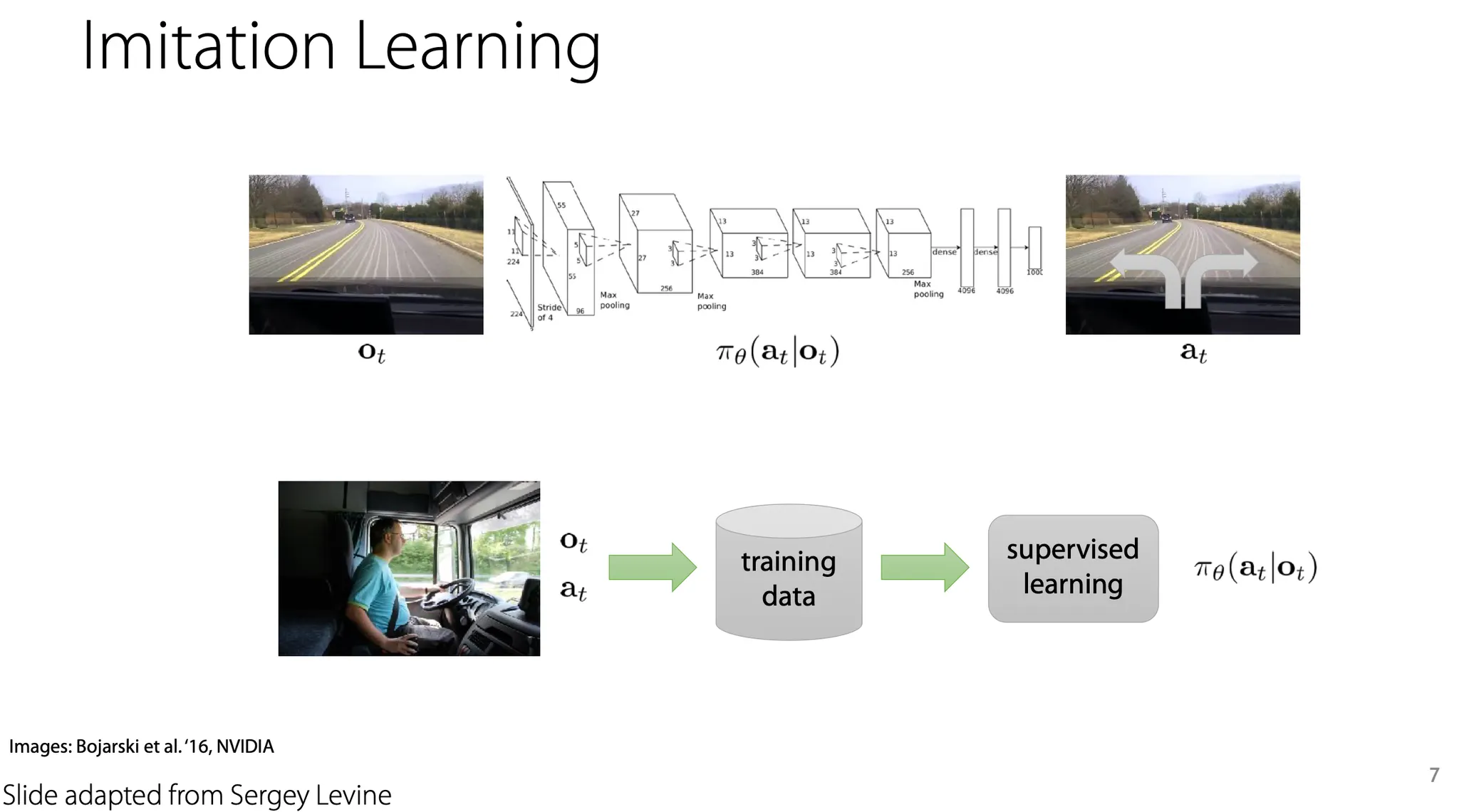
단순한 예로, 사람이 운전하는 것을 그대로 따라하는 imitation learning도 RL의 일종이라고 볼 수 있다.
이런 상황에서는 어떤 policy를 학습함에 있어서 reward는 안전하게 운전하는 경우 높게 주고, 사고가 발생하면 낮게 주는 방식으로 제공할 수 있다.
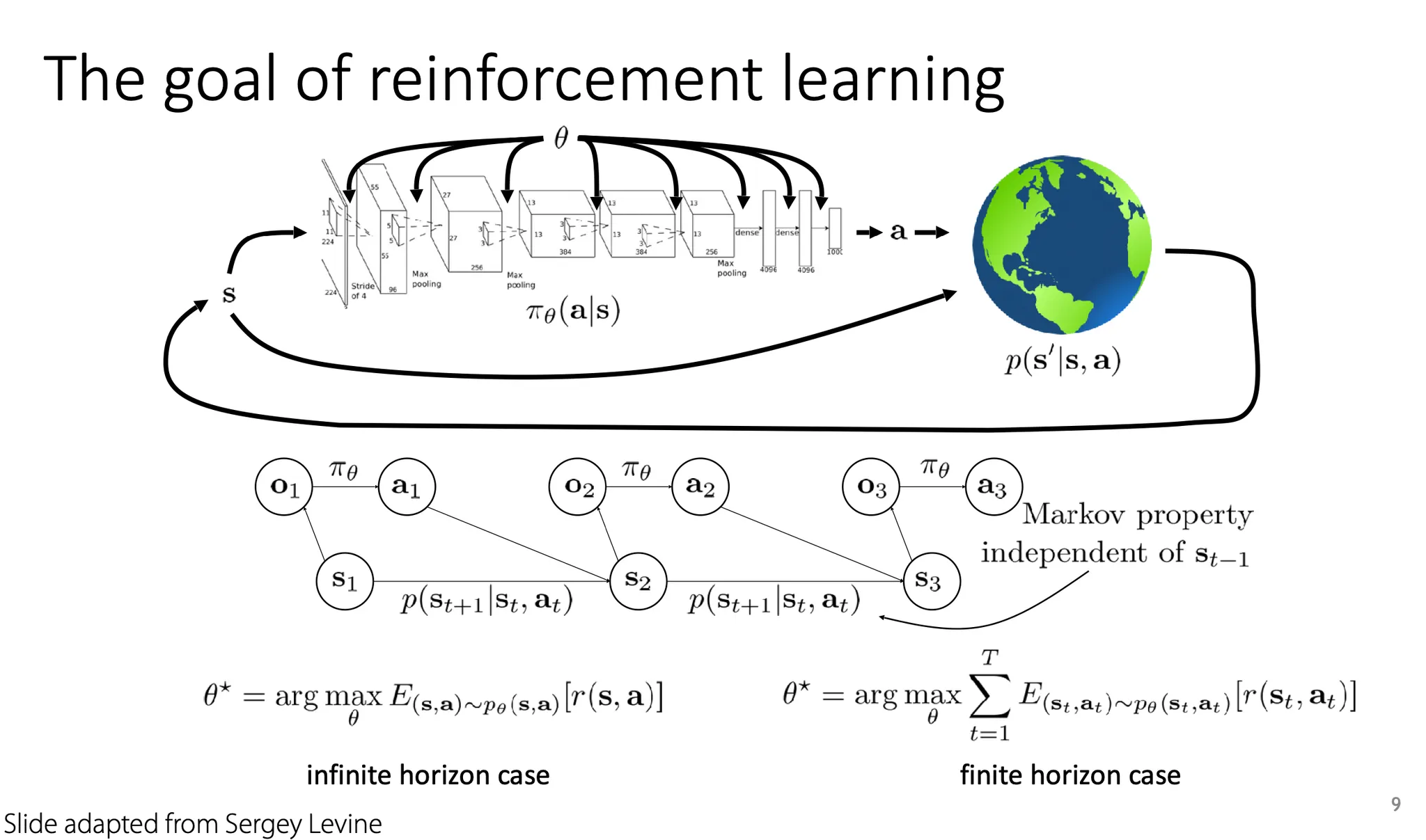
RL의 목표는 policy 를 학습하는 것이다.
Markov property는 reward function과 dynamics가 현재 state에만 의존하고, 이전 state와는 관련이 없다는 것을 의미한다.
Reinforcement learning task를 정의해보자. Supervised learning과 비교해서 생각해보면, RL에서 state space와 action space는 말 그대로 각 time step에서의 state와 action을 정의하기 위한 개념이고, 나머지는 아래 표와 같이 대응된다.
Supervised learning | Reinforcement learning |
data generating distributions | initial state distribution, dynamics |
loss function | reward function |
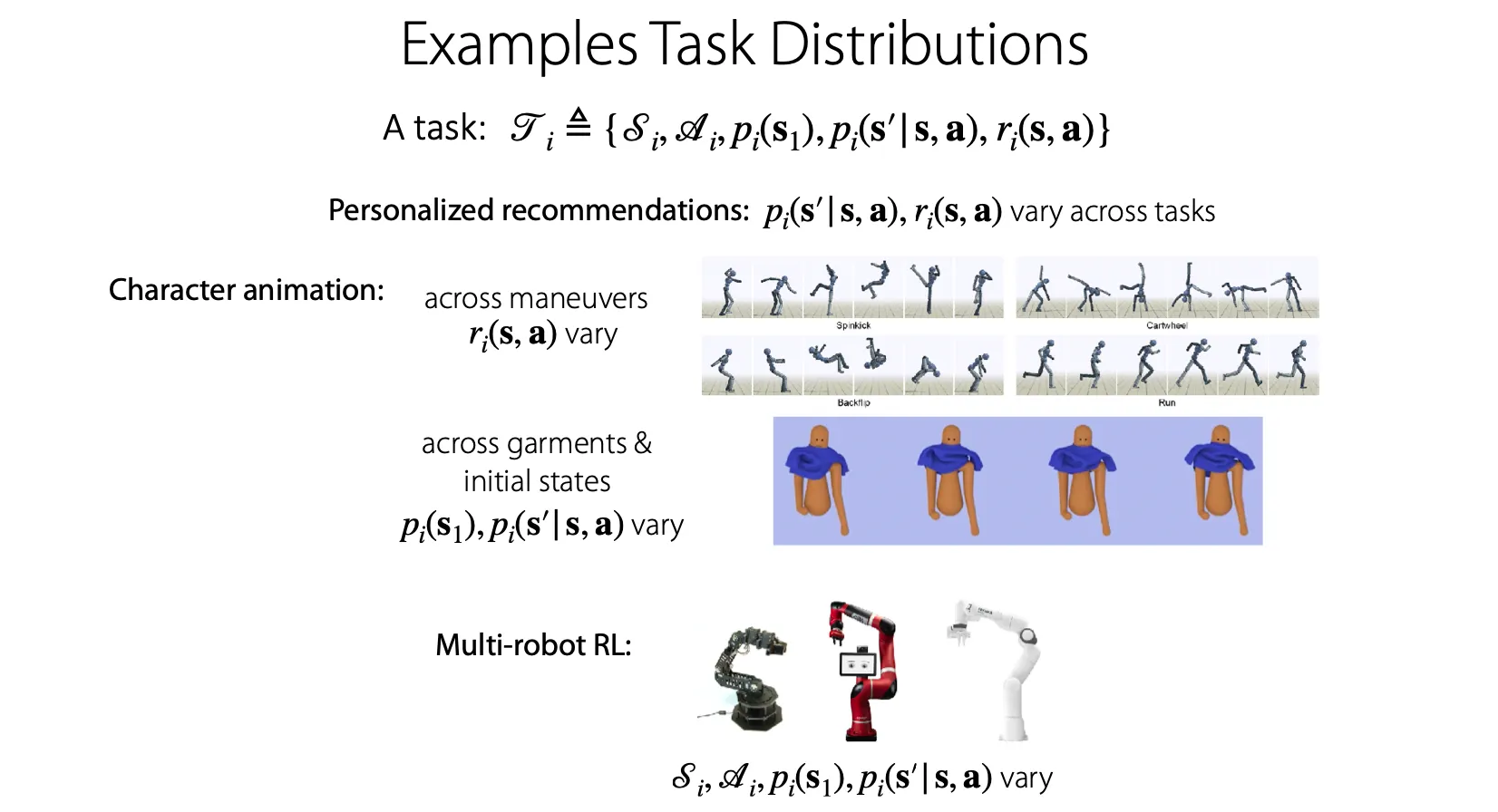
Task distribution의 예시를 들어보자.
Personalized recommendation 문제에서는 각 user에 맞게 추천해주는 것을 각각의 task로 구분할 수 있다.
Character animation 문제에서는 manuever에 따라 reward function이 다른 task들, reward는 같은데 initial state나 dynamics가 다른 task들, state space와 action space까지 다른 task 등 다양한 상황이 있을 수 있다.
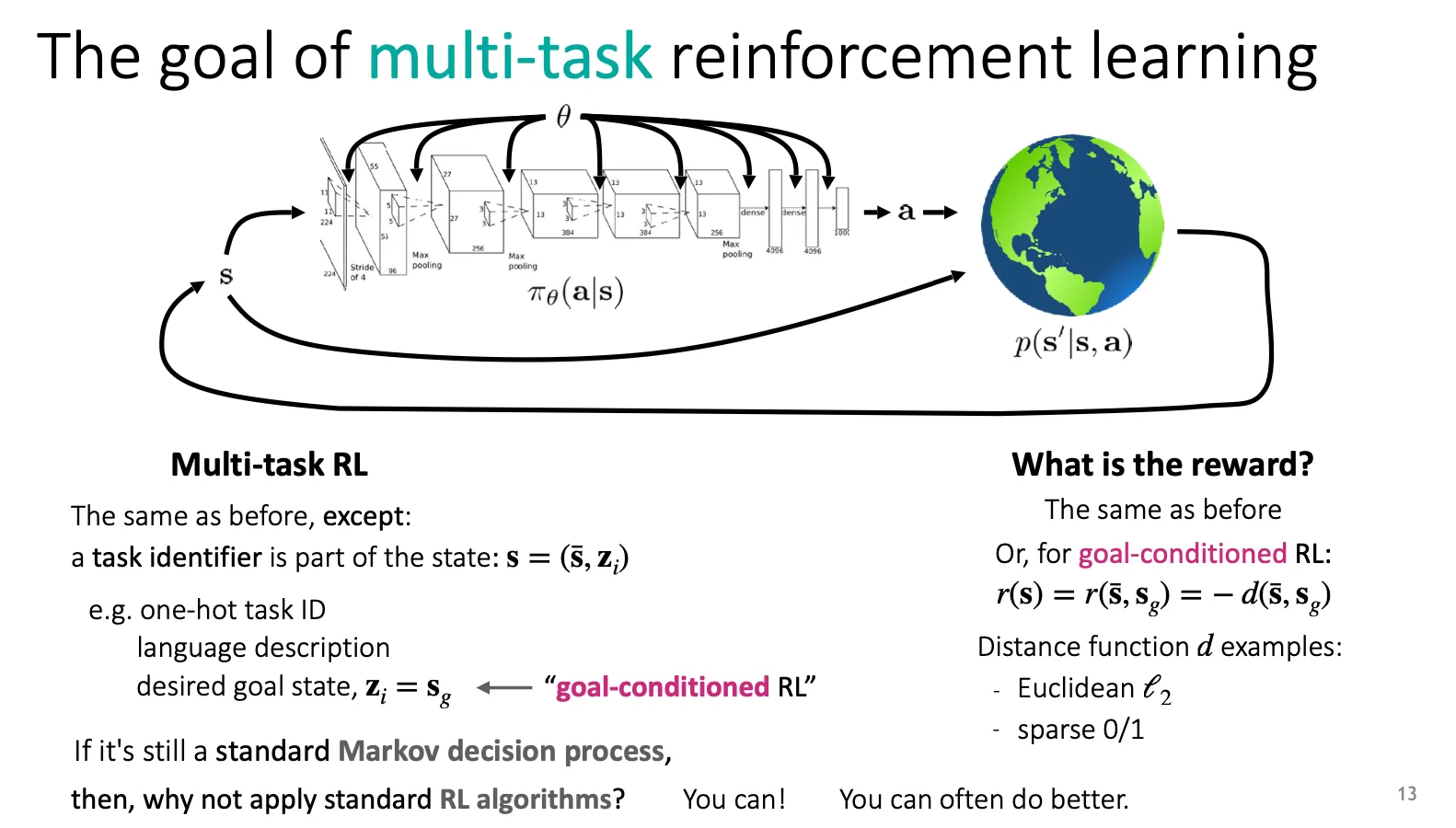
Multi-task RL은 어떻게 표현할 수 있을까?
State의 일부로 task identifier를 도입해보자.
: original state
: task identifier
여러 RL task들을 오른쪽과 같이 union 하면 multi-task RL로 생각할 수 있다.
Multi-task RL은 일반적인 RL과 비슷하지만, state를 정의할 때 어떤 task identifier를 state의 일부로 포함하고 있게 만드는 것이라고 할 수 있다. task identifier의 예시로는 task ID를 one-hot으로 표현하거나, language description을 달아주거나, 목표 state를 기록하는 goal-conditioned RL 등이 있다.
Reward는 일반적인 RL과 동일하게 만들거나, goal-conditioned RL 같은 경우는 goal state와의 거리 등을 이용하여 정의할 수 있다.
여전히 MDP라면, 일반적인 RL algorithm을 적용하는 것으로 충분하지 않을까 생각할 수 있지만, 보통 더 좋은 선택지들을 떠올려볼 수 있다.
Policy gradients & their multi-task/meta counterparts
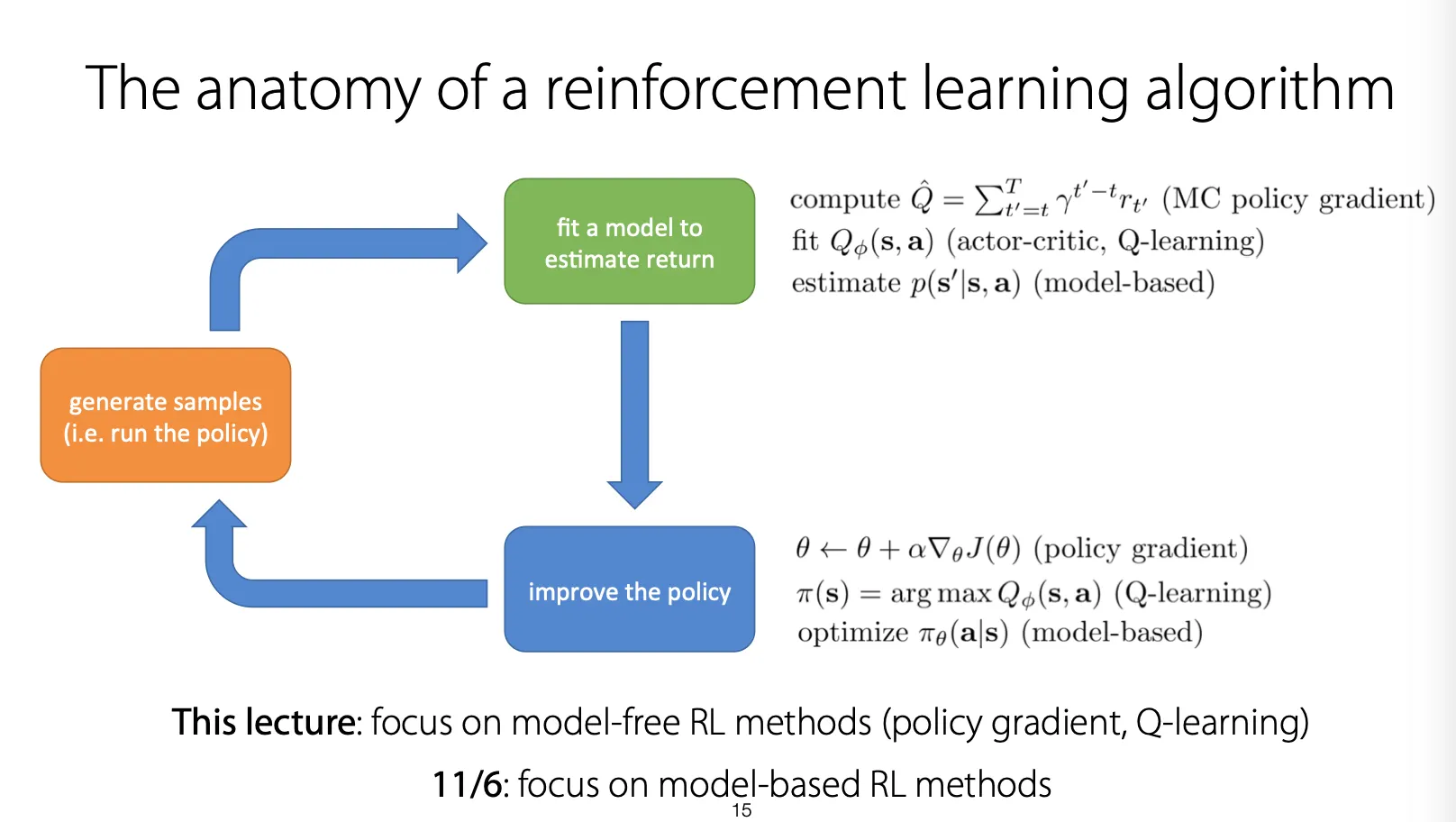
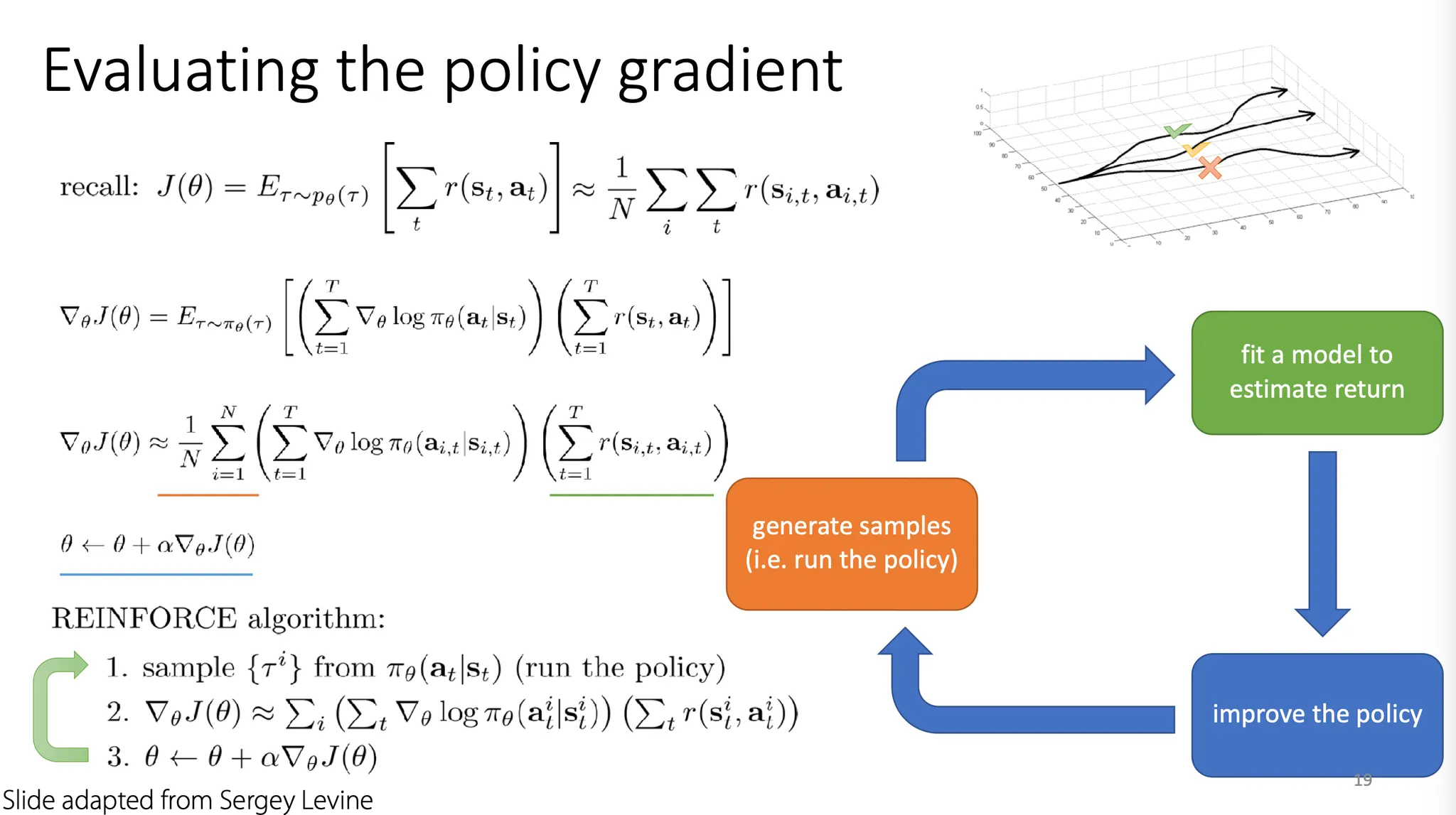
RL algorithm을 분석해보면, policy를 실행해서 sample들을 generate하고, 그 sample들에 대해 model을 fit해서 return을 예측해낸 뒤, 그를 바탕으로 policy를 update하고 다시 sample을 generate하는 구조로 흘러간다. 크게 policy gradient, Q-learning, model-based로 나눌 수 있고, 이번 강좌에서는 policy gradient, Q-learning 관점에서의 RL method들을 주로 다룬다.
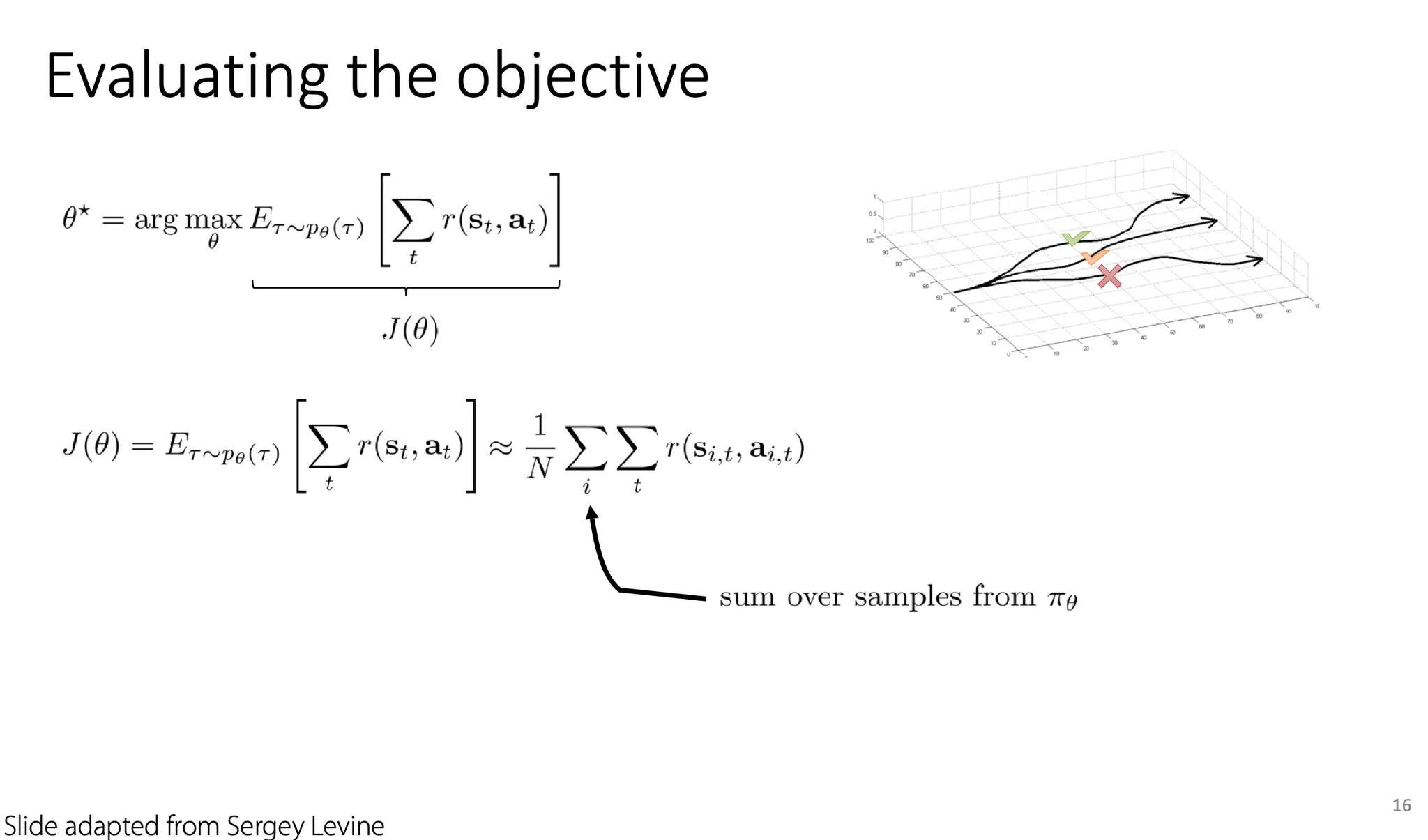
먼저 policy gradient부터 보면, optimal .
Objective: 로 생각할 수 있다.
Objective(policy)의 gradient를 계산하기 위해 전개를 해보면,
로 표현할 수 있다. (기억해둘만한 전개방식인듯!)
이제 각각의 state와 action으로 분리하는게 중요하다.
를 분리하고 를 씌우면, .
이때, 를 계산할 때 과 은 에 의존하는 term이 아니므로 생략하고 정리하면,
오렌지 색으로 밑줄 친 부분이 sample들을 generate하면서 data를 수집하는 단계이고, 녹색으로 밑줄 친 부분이 model을 fit 하고 reward를 계산해내는 부분이다.
파란색으로 밑줄 친 가 policy를 update하는 부분이다.
이를 계속 반복하는 것이 policy gradient 기반의 RL이다.
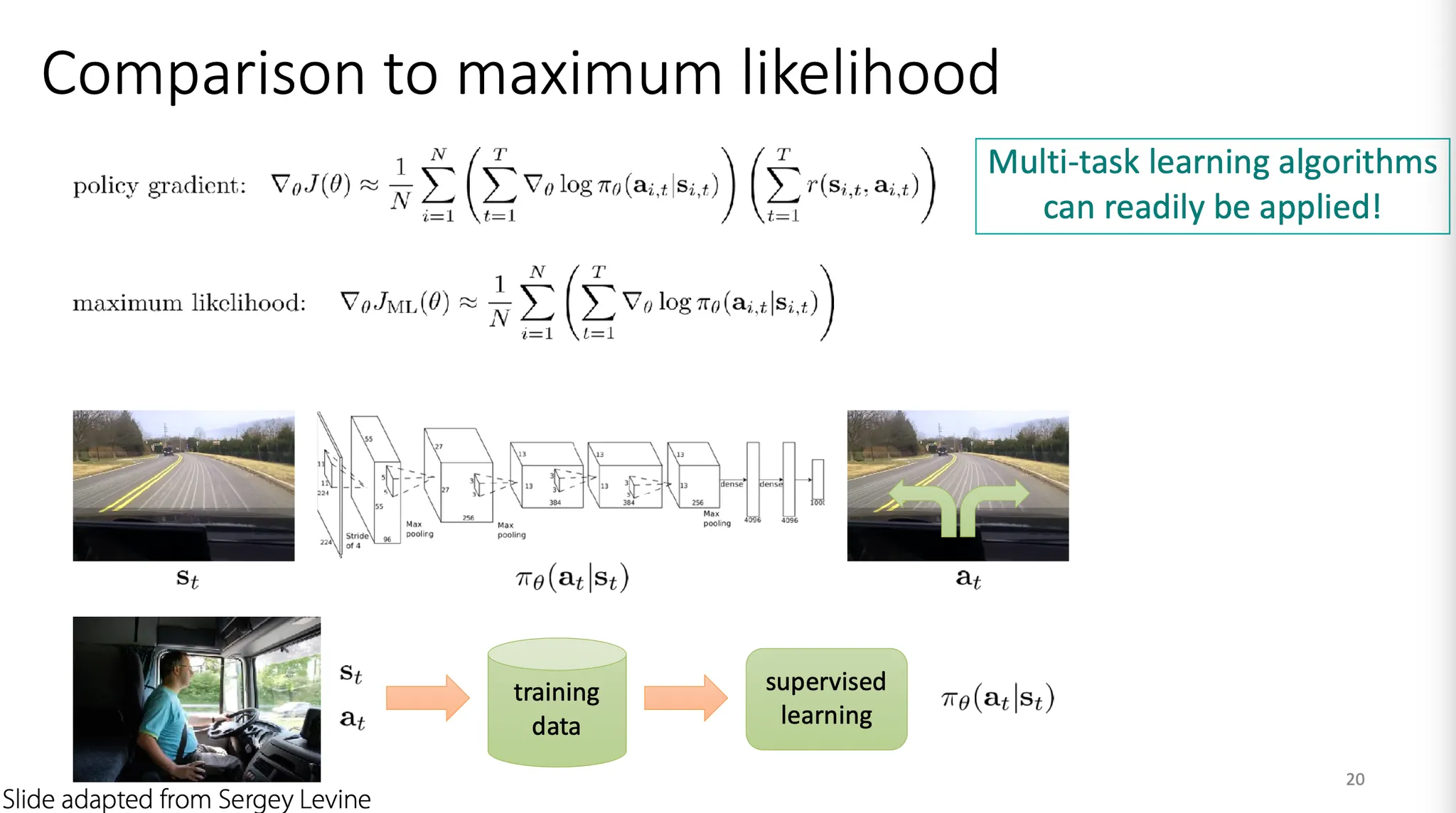
Expert action을 imitation하는 maximum likelihood 와 어떤 점이 다를까? 다른 점은 reward term 뿐이다. 즉, RL에서는 결과적으로 reward가 큰 action들의 probability를 높게 설정하게 된다.
따라서 reward function만 잘 설정해주면 일반적인 multi-task learning algorithm을 꽤 쉽게 적용할 수 있다.
정리하자면, simple maximum likelihood 보다 policy gradient RL은 good stuff(higher reward)를 더 자주 하도록 guide 하는 것과 동일한 것이라고 생각할 수 있다.
그럼 meta learning에도 policy gradient를 쉽게 적용할 수 있을까?
꽤 쉽게 적용 가능하다.
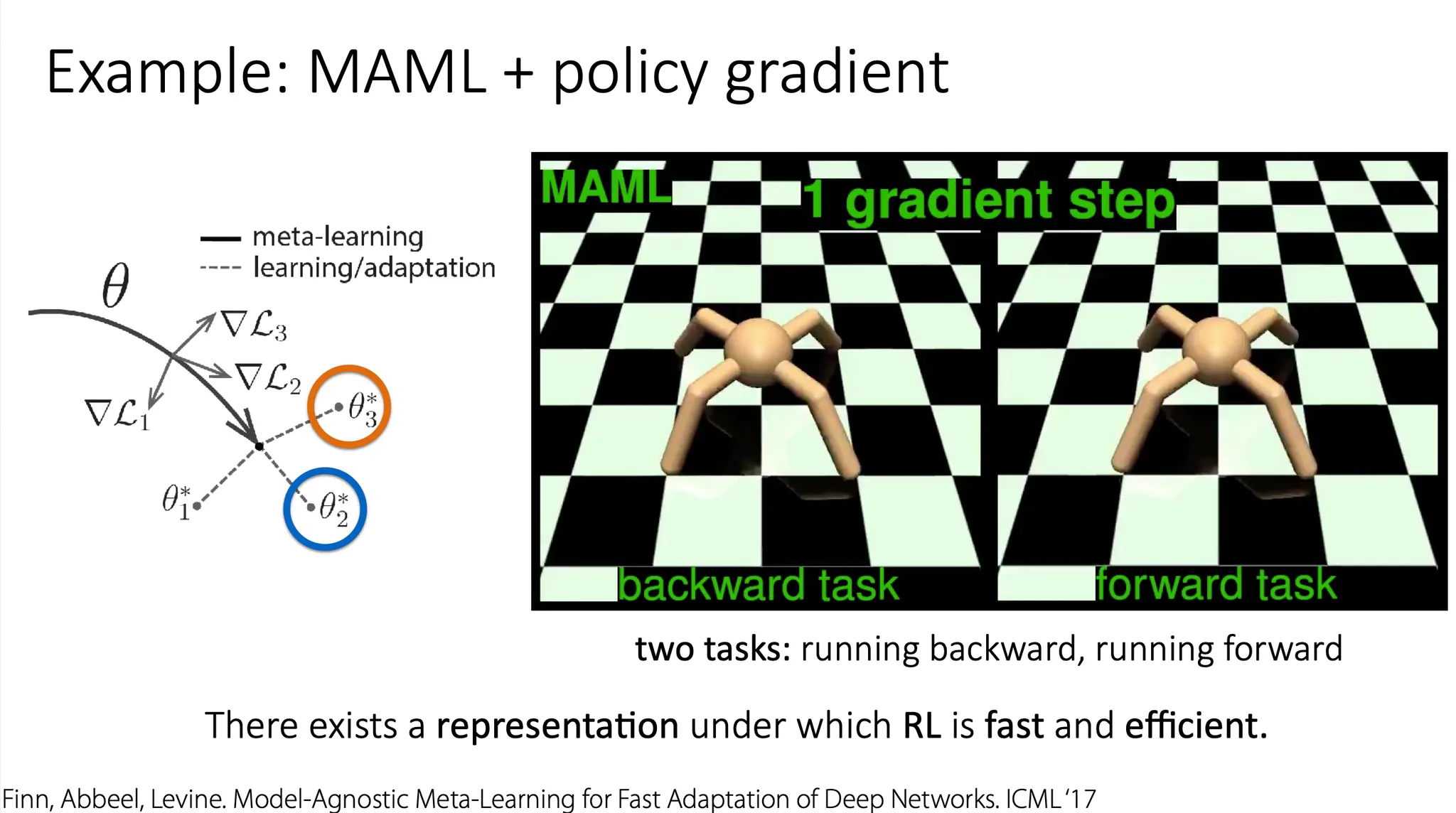
위 예시는 MAML에 policy gradient를 적용한 것으로, 1번의 gradient step만으로도 꽤 괜찮은 성능을 보여주었다. 특정 실험 환경에서는 이렇게 빠르고 효율적인 learning이 가능한 경우가 있다.
Black-box meta-learning의 경우에는 어떨까? 이 경우도 마찬가지이다. 위 예시는 미로를 푸는 meta-learner의 학습에 policy gradient를 적용했다.
Policy gradient의 장단점
장점
•
간단하다.
•
기존의 multi-task / meta-learning algorithm과 쉽게 결합하여 사용할 수 있다.
단점
•
Gradient의 variance가 크다.
◦
Baseline들(GAE, Monte Carlo estimator 등)을 사용하거나 trust region을 적용하는 등으로 일부 해결할 수 있다.
•
On-policy data만 사용할 수 있다.
◦
즉, off-policy가 아니라서 gradient estimate로 기존에 다른 task에서 학습했던 경험을 사용할 수 없다. 현재 policy를 update하려면 현재 policy에서 볼 수 있는 data만 사용할 수 있다. 따라서 sample inefficient 하다.
◦
Importance weight 등의 방법을 사용할 수 있지만, variance가 크다.
Q-learning
Q-learning에서 value function은 특정 state에서 시작하여 time step마다 다른 state로 바뀌는 것이 얼마나 좋은지를 알려주는 함수이다. Q function은 특정 state에서 시작하여 어떤 action을 선택하는 것이 얼마나 좋은지를 알려주는 함수다.
Value function은 action들에 대한 Q function의 expectation이다.
Q function을 알면, 그 정보를 policy를 update 하는데 사용할 수 있다.
State 에서 action 를 선택할 확률이 1이 되도록 하는 action이 나오도록 계속 update하게 된다.
Optimal policy는 Bellman equation을 만족하도록 학습된다.
Fitted Q-iteration algorithm은 다음과 같이 진행된다.
1.
어떤 policy에 따라 data를 수집한다.
2.
를 로 설정한다.
3.
를 로 설정한다.
2, 3번을 K 번 반복하고 update 된 policy를 사용해 1번부터 다시 시작한다.
Q-learning은 off-policy algorithm 이기 때문에 policy가 update되더라도 이전 policy에서부터 나온 data를 재사용할 수 있다.
Q-learning은 gradient descent 방식이 아니라, dynamic programming 방법이라서 meta learning의 MAML 같은 optimization-based나 black-box approach에 적용하기는 어렵다. 하지만 multi-task RL이나 goal-conditioned RL로는 적용이 가능하다.
Multi-task Q-learning
Multi-task learning에 RL을 어떻게 적용할 수 있을까? Policy와 Q-function에 task identifier 를 추가해주면 된다. Multi-task supervised learning에서 stratified sampling이나 weight sharing을 하는 것과 비슷하다. 차이점이 있다면 supervised learning과 달리 data distribution이 주어지지 않고, agent에 의해 생성되며, task에 따라 MDP의 어떤 특성이 변하는지 알 수 있다는 점이다. 여기서 생각해볼 점은 weight sharing 뿐만 아니라 data sharing도 필요한지, 그리고 MDP의 aspect가 바뀌는 점을 어떻게 이용할 수 있을지이다.
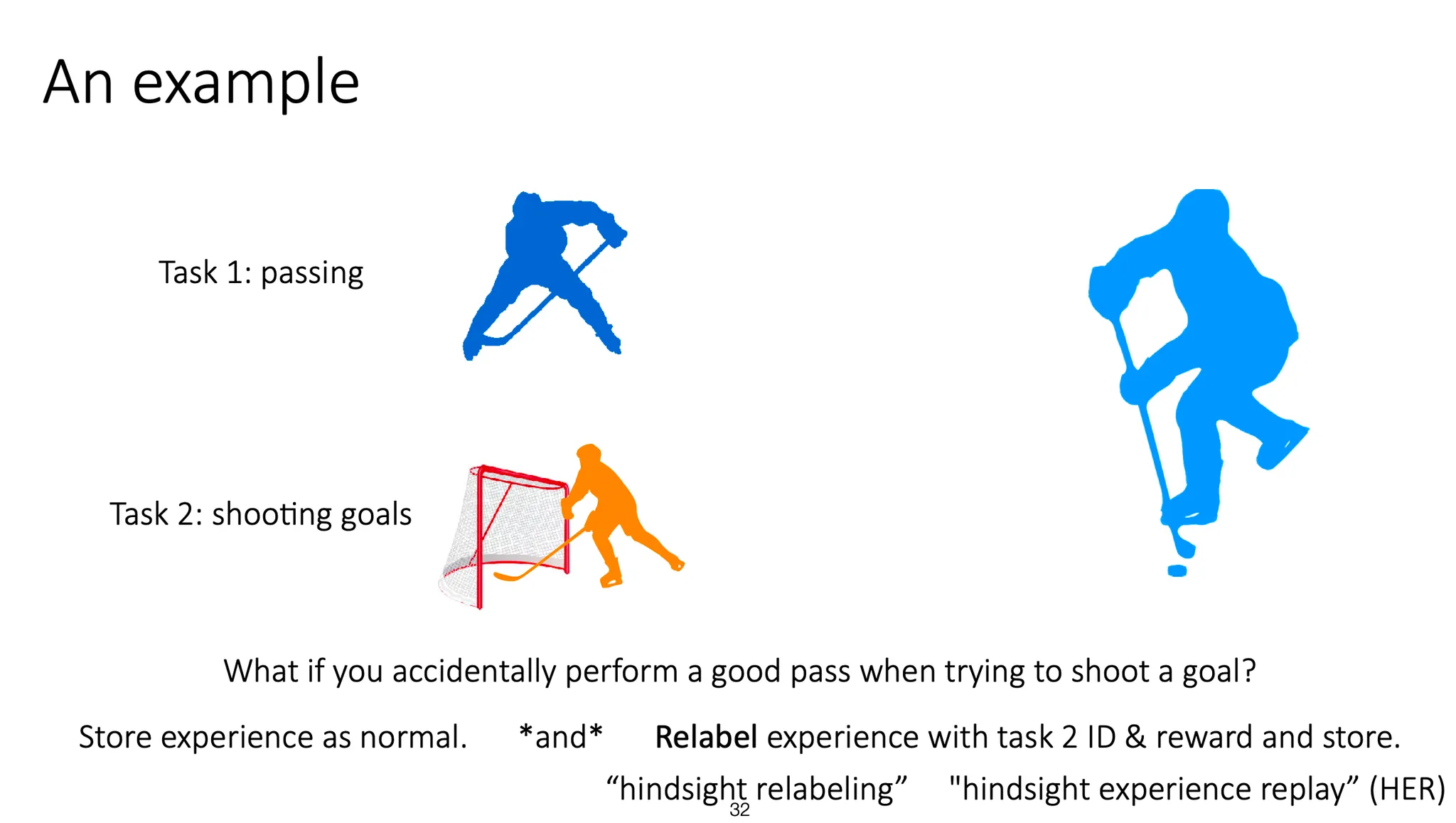
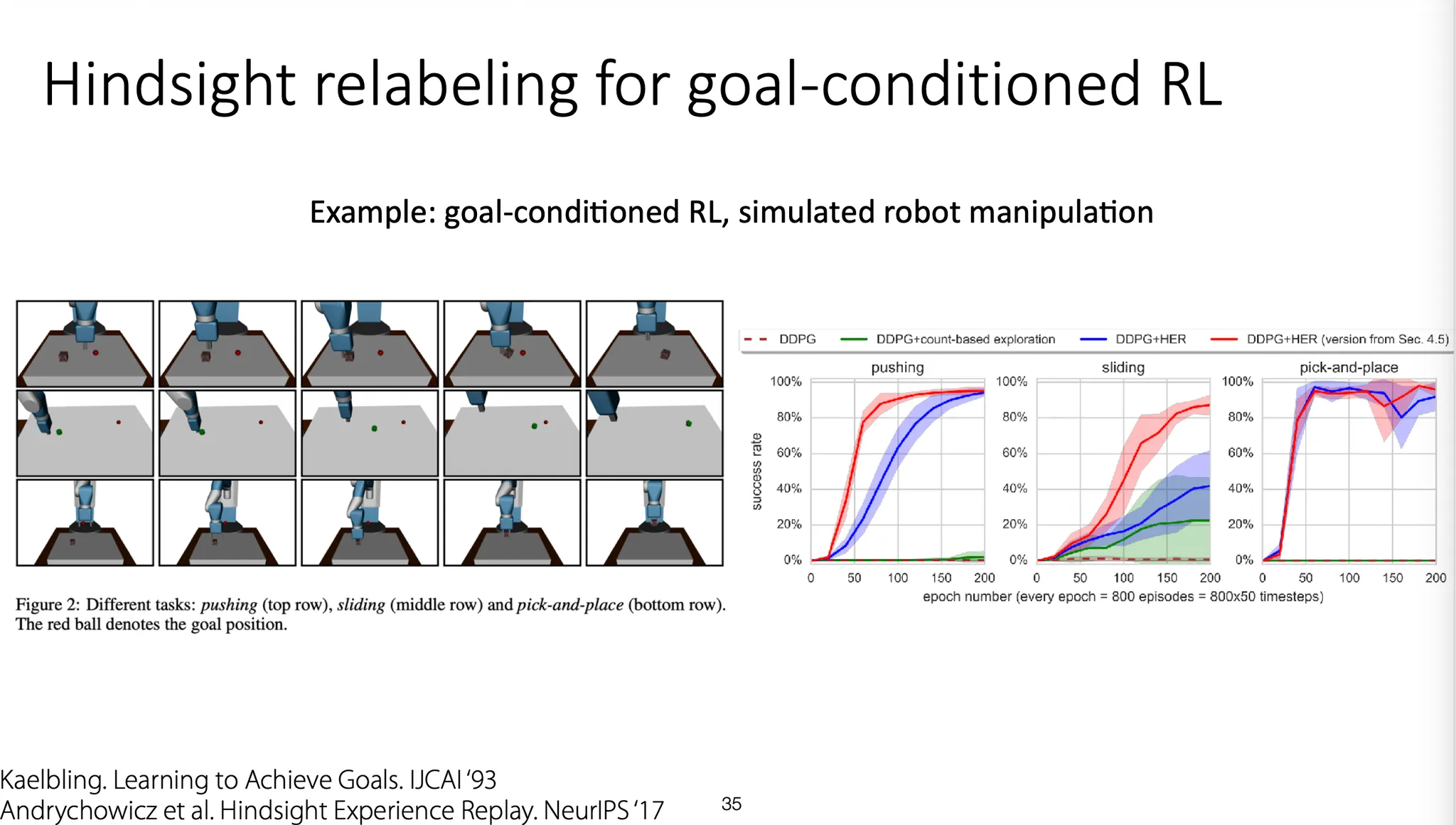
예를 들어, pass를 학습하는 task와 goal shooting을 학습하는 task가 있다고 해보자. 생성된 data가 goal shooting을 목적으로 시도했지만 좋은 pass가 되어버렸다면, 그 data는 저장을 하되, relabeling하여 task 2에서는 bad reward를 부여하고, task 1에서는 good reward를 부여할 수 있을 것이다. 이런 과정을 hindsight relabeling이라고 부른다.
Goal-conditioned RL 상황에서 hindsight relabeling하는 algorithm이다.
원하는 goal state를 보유한 어떤 policy에 따라 data를 생성해내고, 그 data 를 replay buffer에 저장한다.
특정 state(예를 들어, 마지막 state)를 goal로 설정한 뒤 를 relabeling하여 를 만든다. 이를 replay buffer에 저장한다. Replay buffer를 사용해 policy를 update한다.
결과적으로 한 task를 풀고자 할 때, 다른 task(다른 state가 goal인)에 대한 학습도 미리 진행하는 효과가 있다.
Multi-task RL 상황도 Goal-conditioned RL과 비슷하게 학습할 수 있다. 차이점은 goal state를 따로 두는 것이 아니라, task identifier를 바꿔서 relabeling 하는 것이다.
이런 relabeling을 언제 적용할 수 있을까?
우선 reward function이 명확해야 한다. 또한 task가 바뀌어도 dynamics는 크게 변하지 않아야 한다.
그리고 학습 시에는 꼭 off-policy algorithm을 사용해야 한다.
Relabeling 했을 때 훨씬 빠르게 success rate에 도달한다.
Image observation 관련 task들은 어떻게 할까?
Image 간의 distance는 정의하기가 어렵다. L1, L2 distance를 사용하기도 애매하다. 그냥 0/1로 binary reward를 주는 것은 너무 sparse 하긴 하지만, 정확하다고 할 수 있다.
Binary reward를 사용하면, 최종으로 우리가 원하는 state에 도달하는 task에서 agent가 random 하고 unlabel된 interaction을 수행하는 것이 optimal 한 action이 된다. 이 때는 중간 과정이 어떻게 되었든지 상관이 없다.
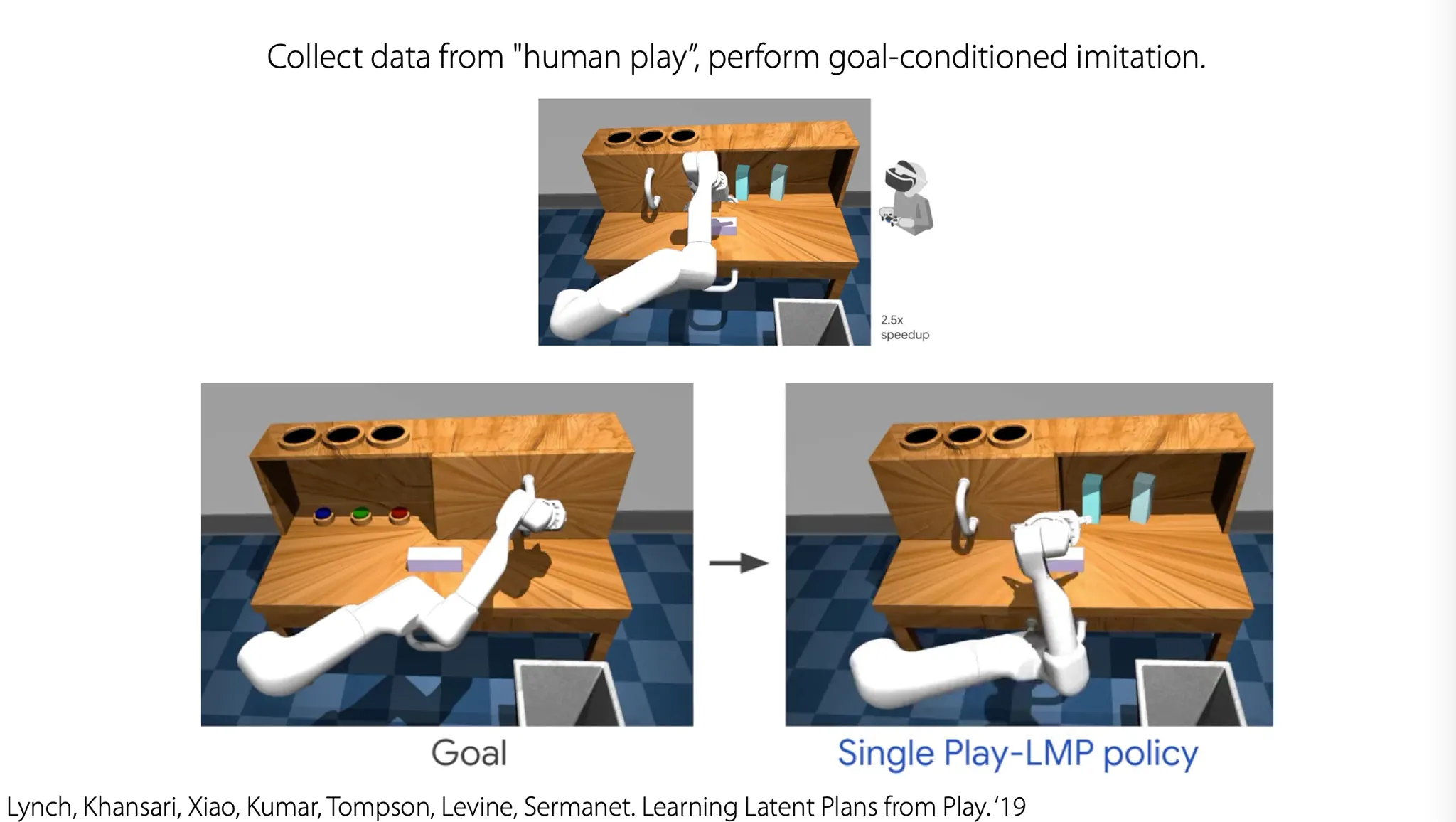
만약 data가 optimal 하다면(예를 들어, imitation learning 상황에서는 human-generated data가 optimal 하다고 가정함), supervised imitation learning을 사용할 수 있다.
우리가 도달하고자 하는 최종 state를 goal로 두고, policy update는 supervised imitation으로 진행할 수 있다.
인간이 수행한 데이터 자체를 goal로 삼고, goal-conditioned imitation을 수행하도록 하면 어떤 reward function이 없더라도 학습이 진행된다.
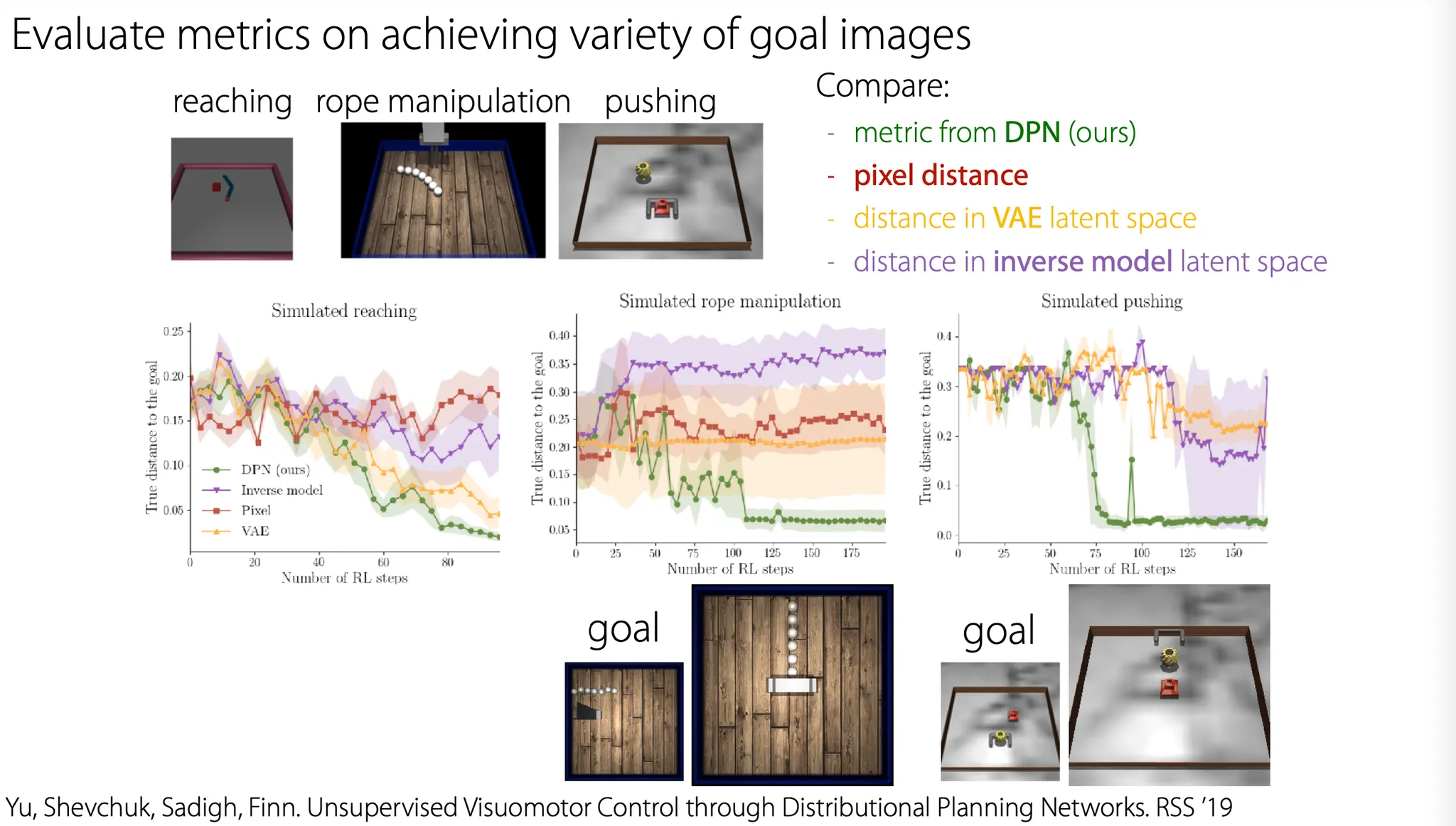
Reward function으로 쓸만한 goal representation을 학습하도록 하는 방법은 없을까?
우선 random noise를 이용해 agent가 무작위로 unlabeled interaction data를 수집하게 한다.
그 후, latent state representation과 latent state model을 학습하는 방법으로 goal state에 도달하는 sequence를 계획하고, goal state에 도달할 경우 그 관측된 sequence를 복원하도록 한다.
Latent space model은 최종적으로는 필요 없고, 학습한 goal representation만 사용하면 된다.
이런 방법을 distribution planning network라고 부른다.
헷갈림... 논문 읽어보기..