Search
Duplicate

[CS330] Lecture 4: Non-parametric(metric-based) Meta-learners

Table of Contents

Optimization-based Meta-Learning

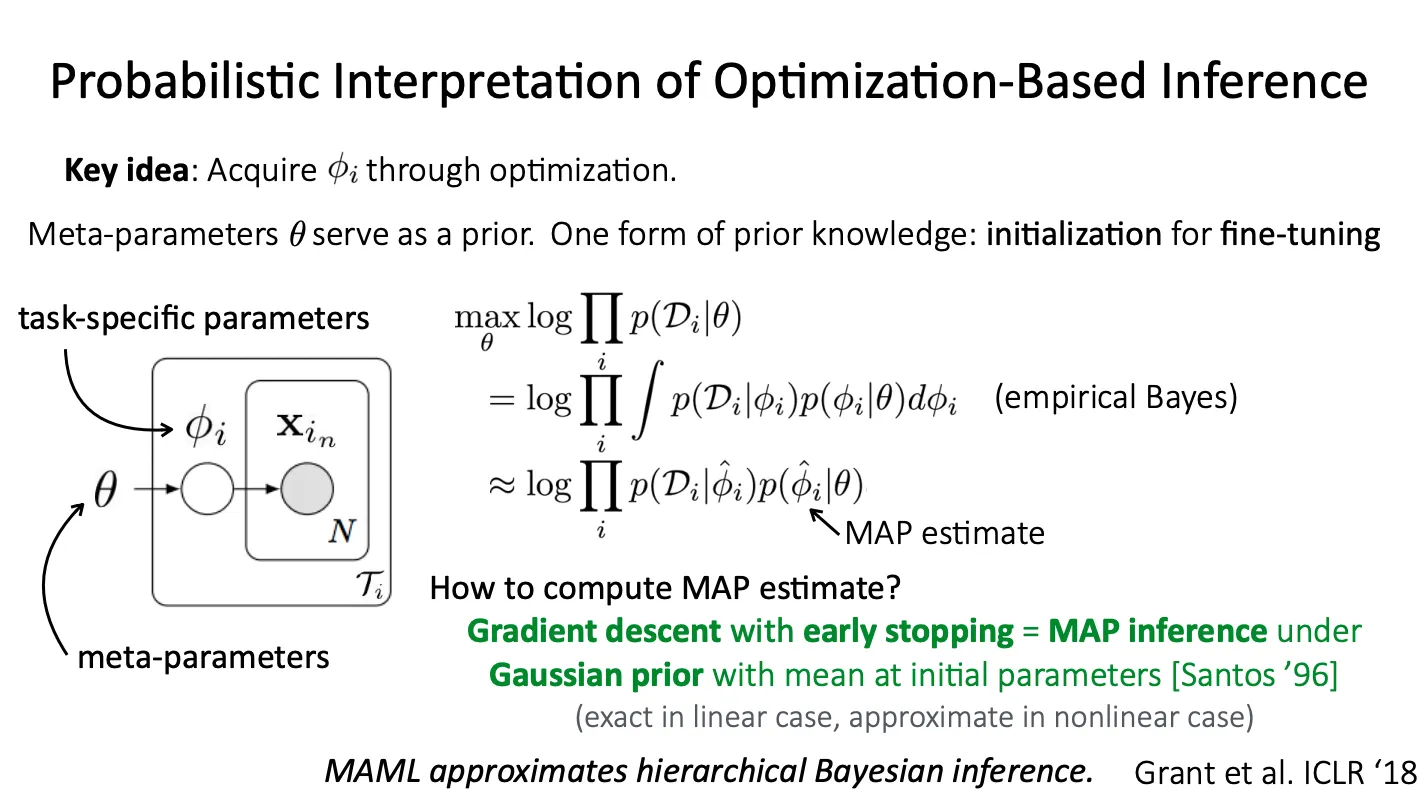
Emperical Bayes

Empirical Bayes:
Procedures for statistical inference in which the prior distribution is estimated from the data.
Standard Bayesian method는 data 관측 전에 prior distribution이 고정되지만empirical Bayes는 data로부터 prior distribution을 estimate한다.
하지만 이를 계산하기 위해서는 integral을 계산해야 하는데, 이는 너무 많은 계산이 필요해 intractable 하다. 따라서 대신 MAP estimate를 사용한다.
MAP estimate는 gradient descent를 끝까지 수행하지 않고 임의의 timestep에서 멈추게 하는 것과 동치이다.
이 estimate는 linear model에서는 exact하고, neural net처럼 non-linear 한 case에서는 approximate이다.

Other priors

MAML에서 사용한 gradient-descent에 early stopping을 적용하는 것은 implicit Gaussian prior를 주는 것이다.
이외에도 prior를 주는 다른 방법들도 있다.

Other challenges

SOTA를 달성하기 위해서 고려해볼만한 사항들
•
How to choose architecture?
Progressive neural architecture search 수행 (Kim et al.)
•
Bi-level optimization can exhibit instabilities
◦
Inner learning rate는 자동으로 학습되도록 하고, outer learning rate는 tuning 해주기 (AlphaMAML)
◦
Inner loop의 parameter의 일부만 optimize (CAVIA)
◦
각 iteration 마다 inner learning rate와 batch normalization 다르게 (MAML++)
◦
Context variable을 추가로 사용해 expressive power를 끌어올림 (CAVIA)
•
Back-propagating through many inner gradient steps is compute- & memory-intensive
◦
dϕidθ\frac{d\phi_i}{d\theta}를 identity로 두고, first order 까지만 계산 (First-order MAML, Reptile)
▪
간단한 few-shot task까지는 꽤 잘 적용되지만, 복잡한 meta-learning task에는 잘 안 됨.
◦
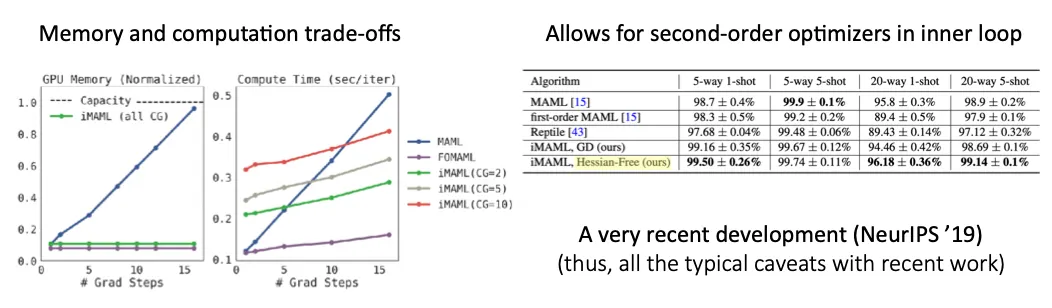
Implicit function theorem을 사용해 meta-gradient 계산 (Implicit MAML)
즉, λ2∥ϕ′−θ∥2\frac{\lambda}{2}\|\phi' - \theta\|^2 term을 추가하여 mean을 θ\theta로 하는 Gaussian regularization을 더 해줌.
ϕ=U(θ,Dtrain)=arg min⁡ϕ′L(ϕ′,Dtrain)+λ2∥ϕ′−θ∥2\phi = \mathcal{U}(\theta, \mathcal{D}^{\text{train}}) = \argmin_{\phi'} \mathcal{L}(\phi', \mathcal{D}^{\text{train}}) + \frac{\lambda}{2}\|\phi'-\theta\|^2
U\mathcal{U}: update procedure
이때, G(ϕ′,θ)=arg min⁡ϕ′L(ϕ′,Dtrain)+λ2∥ϕ′−θ∥2G(\phi', \theta) = \argmin_{\phi'} \mathcal{L}(\phi', \mathcal{D}^{\text{train}}) + \frac{\lambda}{2}\|\phi'-\theta\|^2로 두면,
∇ϕ′G(ϕ′,θ)∣ϕ′=θ=0\nabla_{\phi'} G(\phi', \theta)\vert_{\phi'=\theta} = 0
∇ϕ′L(ϕ′)+λ(ϕ′−θ)=0\nabla_{\phi'}\mathcal{L}(\phi') + \lambda(\phi' - \theta) = 0
ϕ′=θ−1λ∇ϕ′L(ϕ′)\phi' = \theta - \frac{1}{\lambda}\nabla_{\phi'}\mathcal{L}(\phi')
dϕ′dθ=I−1λ∇ϕ′2L(ϕ′)dϕ′dθ\frac{d\phi'}{d\theta} = I - \frac{1}{\lambda}\nabla^2_{\phi'} \mathcal{L(\phi')}\frac{d \phi'}{d \theta}
dϕ′dθ=(I−1λ∇ϕ′2L(ϕ′))−1\frac{d\phi'}{d\theta} = (I - \frac{1}{\lambda}\nabla^2_{\phi'} \mathcal{L(\phi')})^{-1}
따라서 1λ∇ϕ′2L(ϕ′)\frac{1}{\lambda}\nabla^2_{\phi'} \mathcal{L(\phi')}, final optimization point의 Hessian만 계산하면 되고 inner optimization process 전체를 미분해서 계산하지 않아도 된다.
이 term을 계산할 때 conjugate gradient를 계산하는데, iteration을 많이 수행할수록 exact하게 될 것 이고, iteration을 전혀 하지 않으면 first-order MAML과 동치이다.
즉, optimization path 전체에 대해 differentiate 하지 않아도 됨.

Takeaways - 장단점

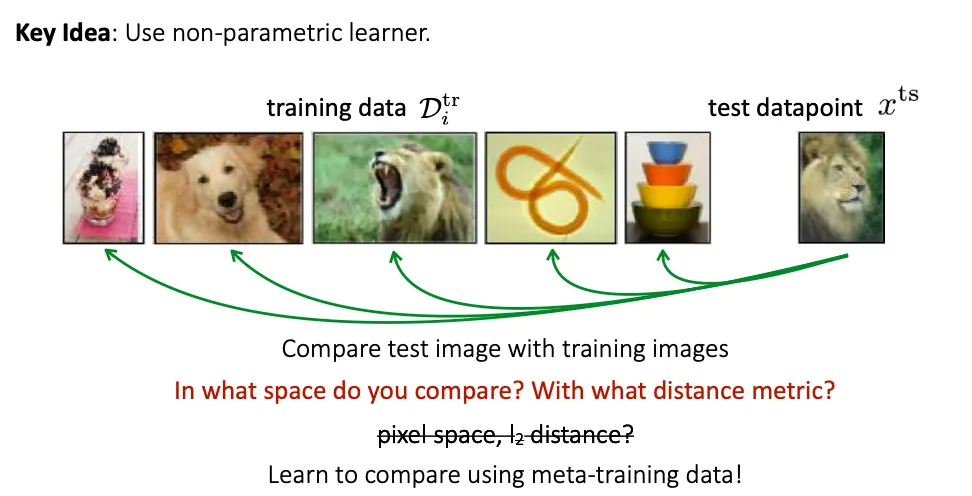
Non-parametric Few-shot Learning

ex) Siamese networks, Matching networks, Prototypical networks
Non-parametric learner 를 생성해낼 수 있는 parametric meta-learner 를 만들 수 있을까?

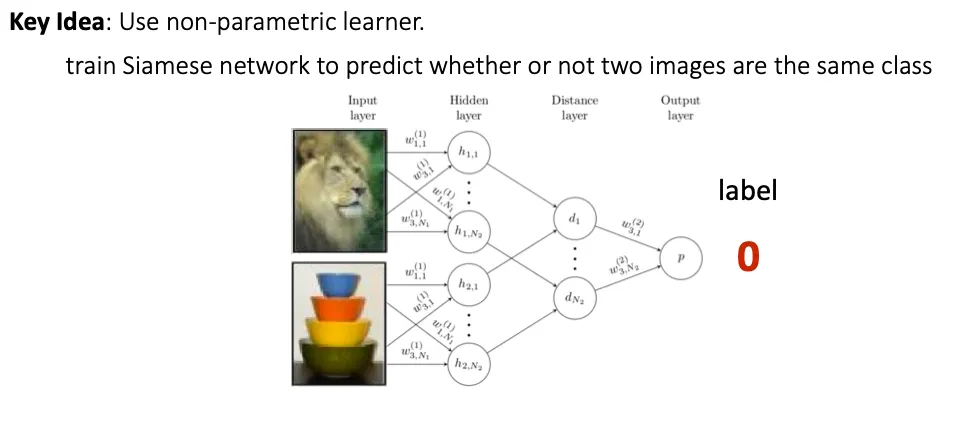
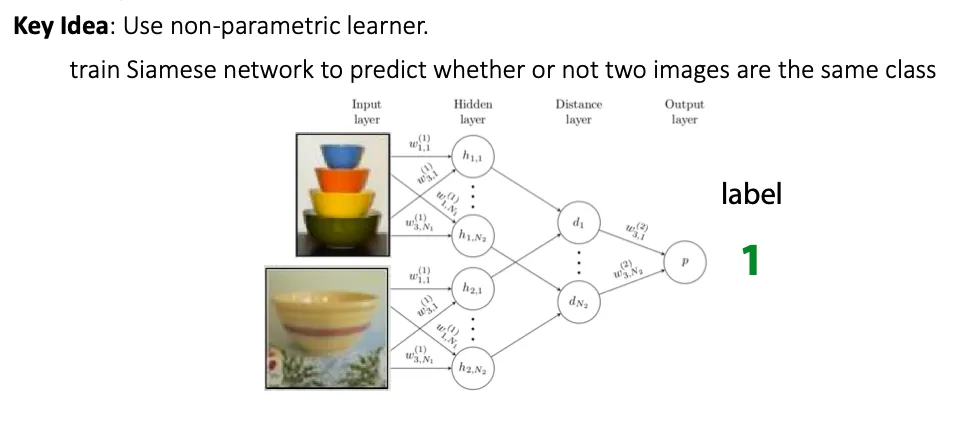
Siamese Network

Siamese network는 두 input image들을 비교해서 같은 class 이면 1, 다른 class 이면 0을 output 하도록 했다.
그런데 Meta-training 시에는 binary classification을 수행하고, meta-test에서는 N-way classification을 수행하게 된다. 이를 match 할 수 있을까? → Matching networks

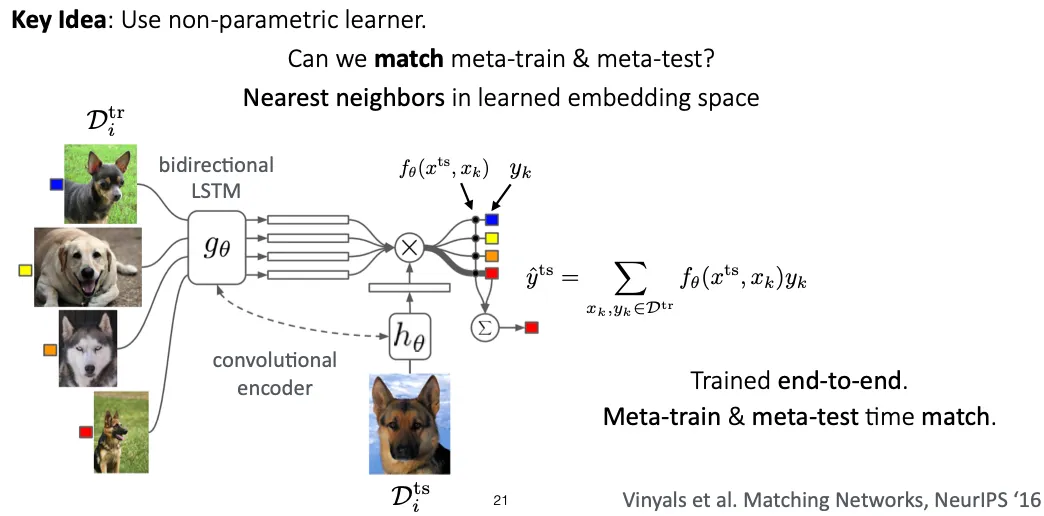
Matching Networks

CS330 Lecture 4 slide
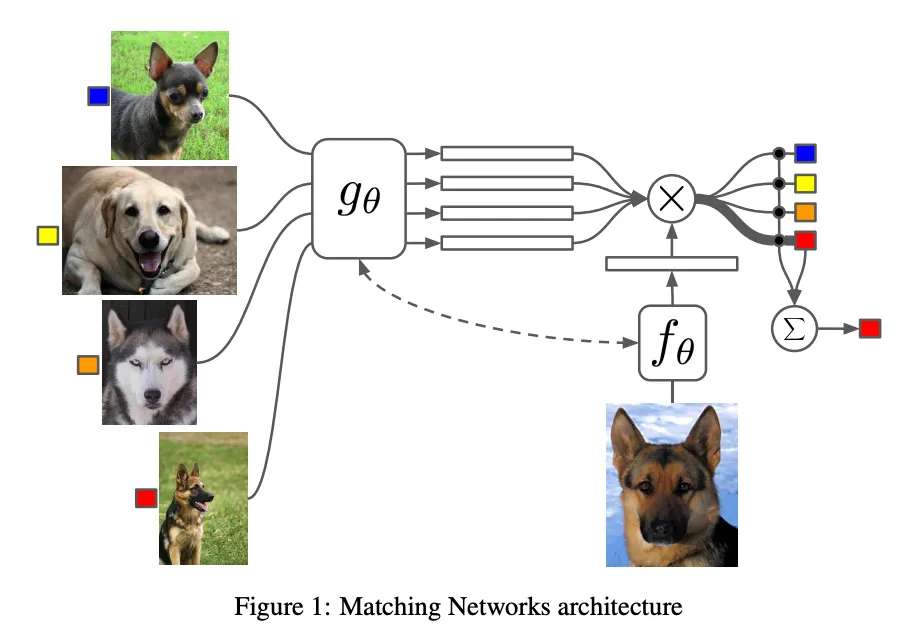
Matching Networks
y^=∑i=1ka(x^,xi)yi\hat{y} = \sum^k_{i=1}a(\hat{x}, x_i)y_i
a(x^,xi)=ec(f(x^),g(xi))∑j=1kec(f(x^),g(xi))a(\hat{x}, x_i) = \frac{e^{c(f(\hat{x}), g(x_i))}}{\sum^k_{j=1}e^{c(f(\hat{x}), g(x_i))}}
먼저 Attention kernel aa 를 통해 xix_i와 x^\hat{x}의 유사도(cosine similarity)를 구하여 softmax를 취한 값을 weight로 삼는다. 이 weight를 각 xix_i의 label인 yiy_i와 곱해서 x^\hat{x}의 label이 무엇이 될지의 확률을 weighted sum으로 구한다.
이때 f, g는 CNN 등의 feature extractor이다.
Support set 전체를 고려해주기 위해 bidirectional LSTM을 추가로 사용했다.
f(x^,S)=attLSTM(f′(x^),g(S),K)f(\hat{x}, S) = \text{attLSTM}(f'(\hat{x}), g(S), K)

Algorithms of Non-parametric methods

Non-parametric approach에서는 parameter ϕ\phi 가 없고 그냥 deterministic 하게 계산된다.
One shot 보다 많다면 어떻게 해야할까? → 해당 class의 prototype을 정하고, 그걸 비교하면 어떨까? → Prototypical Networks

Prototypical Networks

Properties of Meta-Learning Algorithms

세 접근 방식 모두 computation graph 관점에서 해석할 수 있고, 서로 mix & match 할 수도 있다.