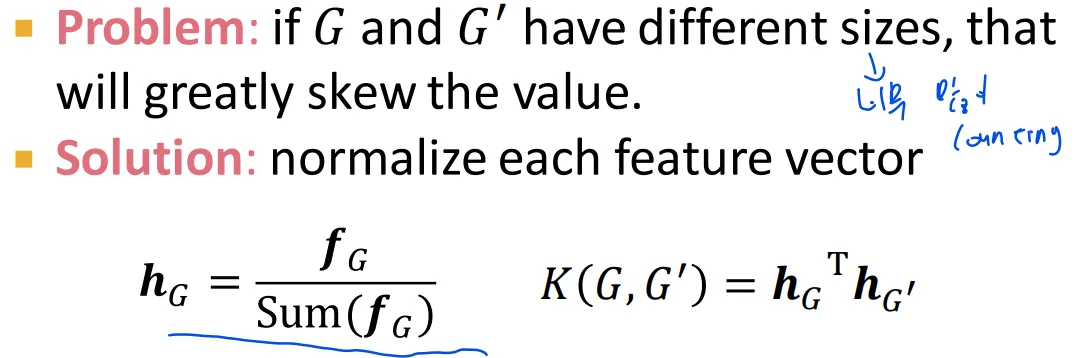Traditional Methods for Machine Learning in Graphs
•
Traditional ML pipeline
◦
기존 ML은 데이터(feature) x에서 y가 나옴
◦
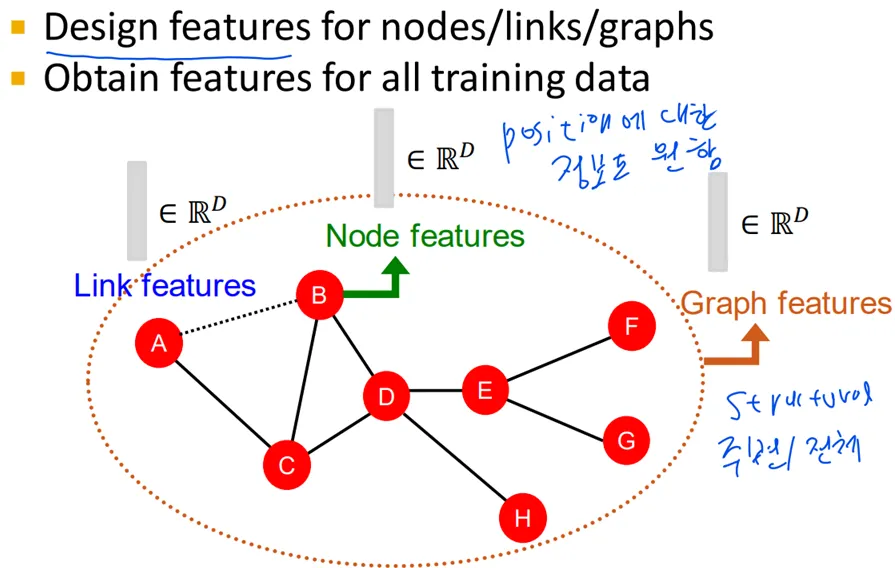
Grpah를 어떻게 데이터(feature)화 시킬지에 대한 고민이 필요
◦
Global하게 structural한 특성을 볼 수도 있고, local하게 볼 수도 있음
Node-Level Tasks and Features
•
Node-level task overview
◦
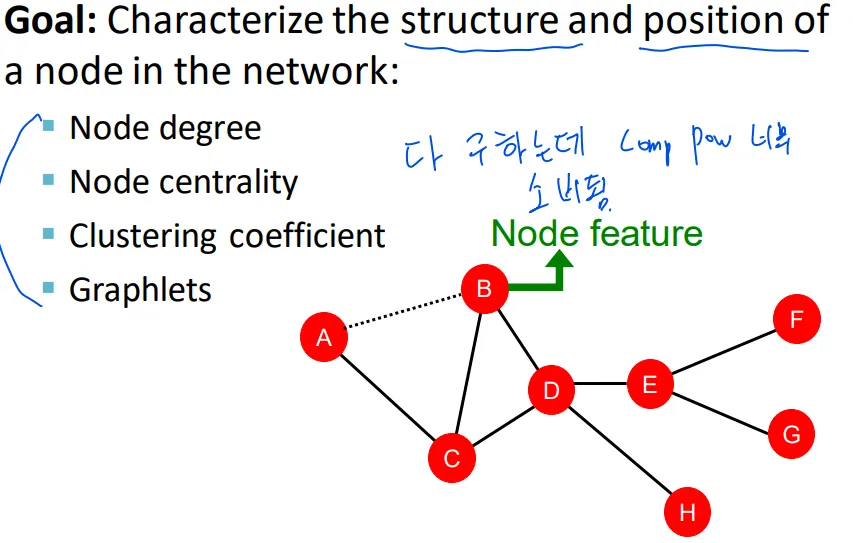
Node-level의 feature를 얻으려 함. 간단하게 보면 node degree도 feature로 볼 수 있음
◦
Node degree는 node 구분이 어려운 문제가 있음. C랑 E가 둘다 degree가 3임
•
Node centrality
◦
Eigenvector centrality
▪
Eigenvector centrality는 내 주위에 중요한 node가 있으면 나도 중요하다는 뜻
▪
내 중요도가 이웃들의 중요도에도 영향을 미치기 때문에 recursive하게 구할 수도 있고, 식 형태를 행렬로 표현하면 그게 eigen vector를 구하는 거랑 같아서 eigen vector 구하는 문제로 바꿀수도 있음
◦
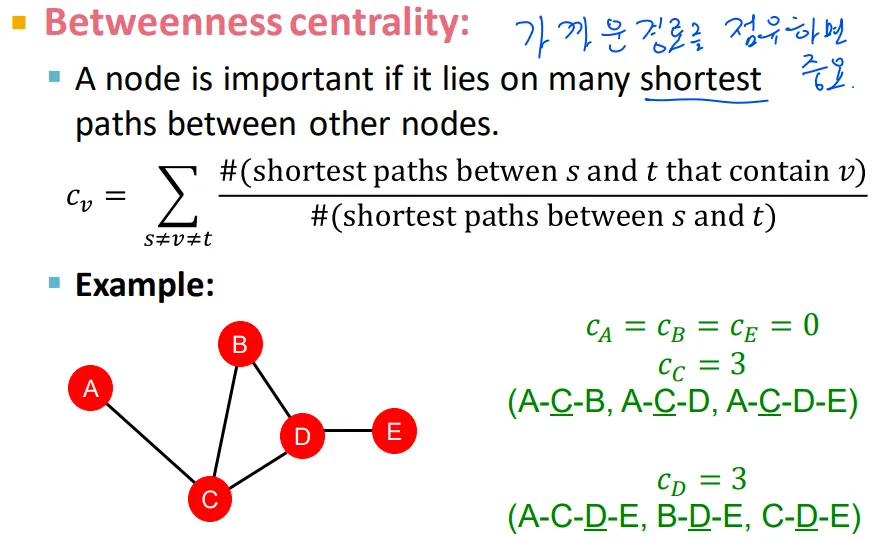
Betweenness centrality
▪
Node 사이의 최단 경로에 내가 포함되면 betweenness centrality 증가
◦
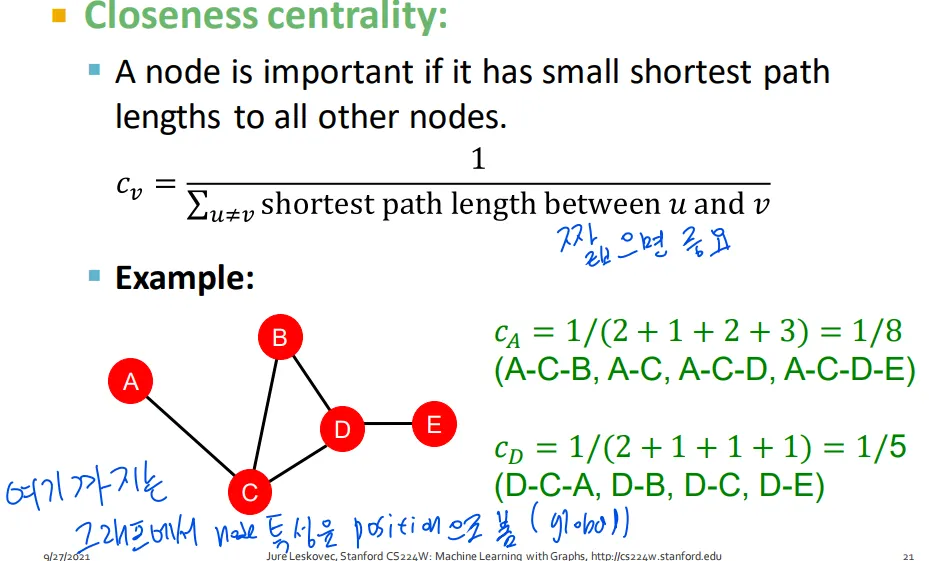
Closeness centrality
▪
내가 다른 node랑 가까우면 closeness centrality 증가
•
Node features
◦
이제 local한 position에 대한 feature를 생성
◦
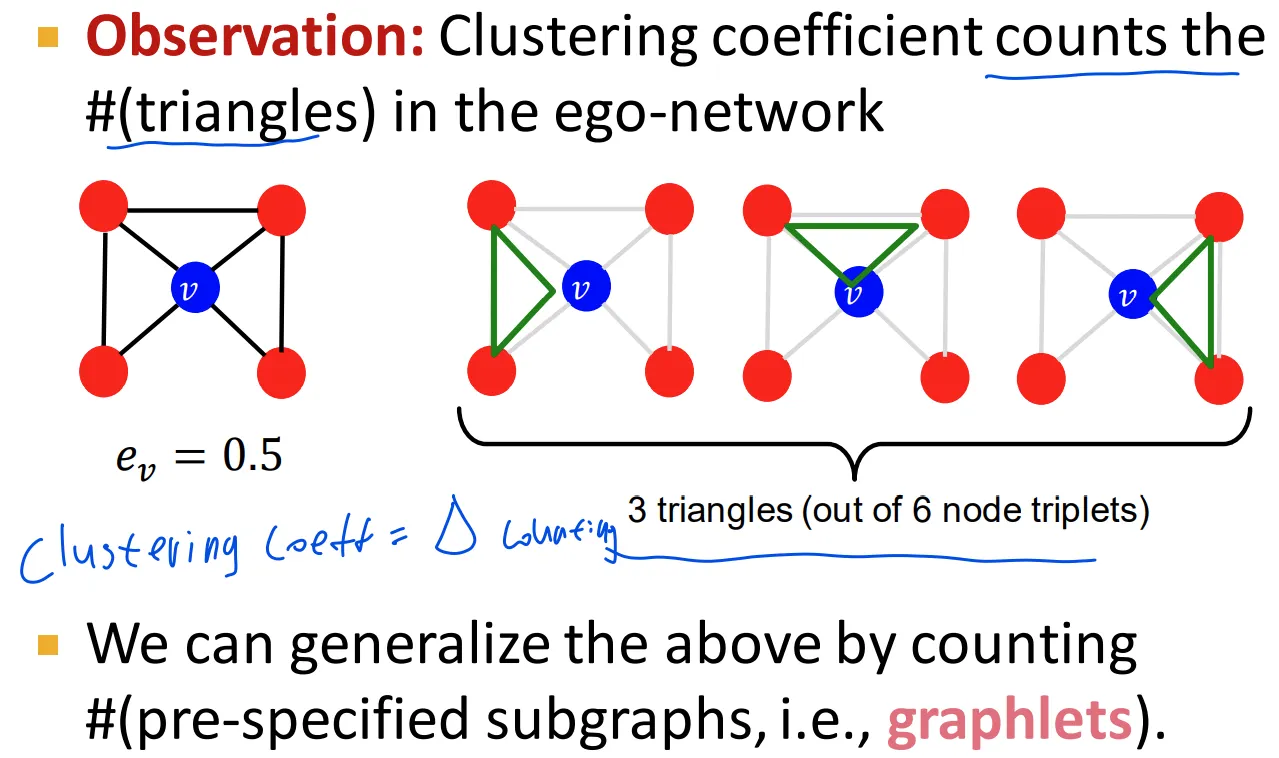
Clustering coefficient
▪
내 친구들은 서로 친구인가? 친구이면 clustering coefficient 상승. 내 주위의 triangle counting과 같은 문제
▪
마치 내 주위의 subgraph를 counting하는 것 같고, 이는 graphlet과 연결됨
◦
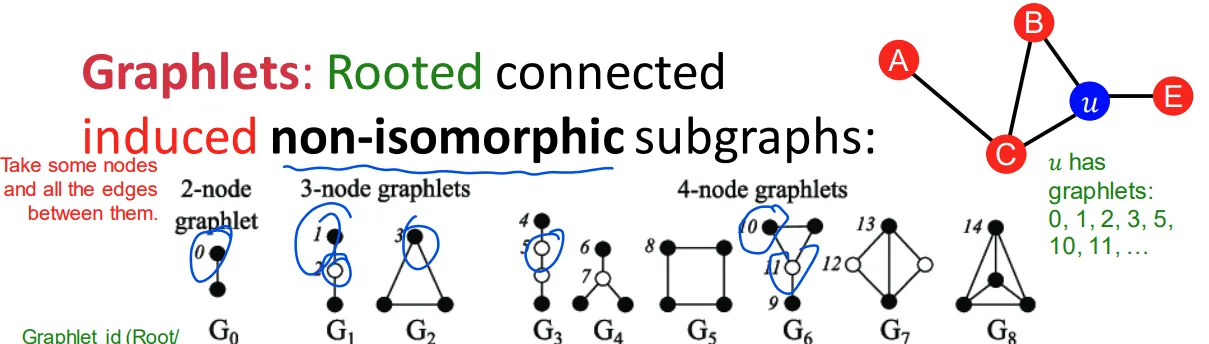
Graphlets
▪
Induced subgraph는 기존 graph에서 일부 node와 일부 node들 사이 edge를 그대로 가져온 것
▪
Graph isomorphism은 연결 상태가 동일한 그래프인지 아닌지를 나타냄
▪
4-hop에는 73개의 가능한 graphlet 존재, 이 graphlet counting으로 feature를 만들 수 있음
▪
Counting 결과가 graphlet degree vector (GDV)
•
지금까지의 내용은 모두 structure-based features
Link Prediction Task and Features
•
Formulation
◦
기존에 있는 link를 지우고 해당 link를 예측하게 문제 설정
◦
이 다음 time step의 link를 예측하게 문제 설정 (3D simulation의 graph evolution)
•
단순화 하기
◦
간단한 모델로는 node 사이의 # of common neighbors를 구해서 그 수가 큰대로 link 만들수도 있음
•
Distance-based feature
◦
두 node 사이의 최단 거리를 feature로 설정. 하지만 이는 가능한 연결의 개수는 반영 못함
•
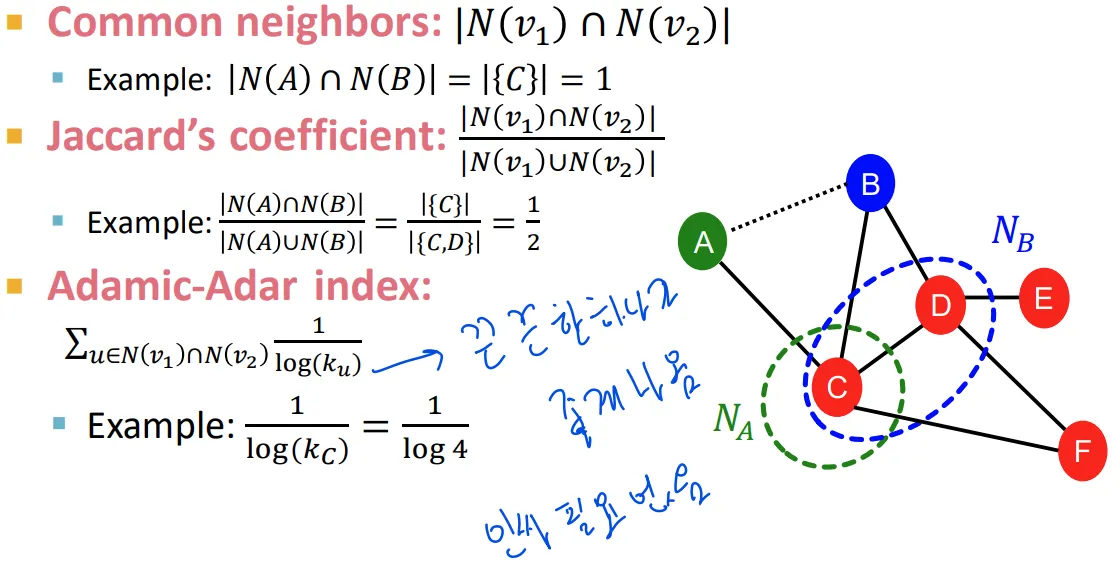
Local neighborhood overlap
◦
두 node 사이의 # of shared node를 카운팅
◦
하지만 공통 이웃이 없으면 feature가 없어지는 문제 발생
•
Global neighborhood overlap
◦
multi-hop에서도 working하는 feature 필요
◦
Katz index 활용. 두 node 사이의 가능한 walks 조합을 파악
◦
등비급수의 합으로 볼 수 있고, 등비급수 합 공식에 따라서 식 변형 가능. 다만 발산하거나 할 경우에는 존재 안할수도 있음
Graph-Level Features and Graph Kernel
•
Kernel methods
◦
Kernel matrix가 모두 양이면서, 각각 라는 함수를 취한 것의 내적이 되게 설정
•
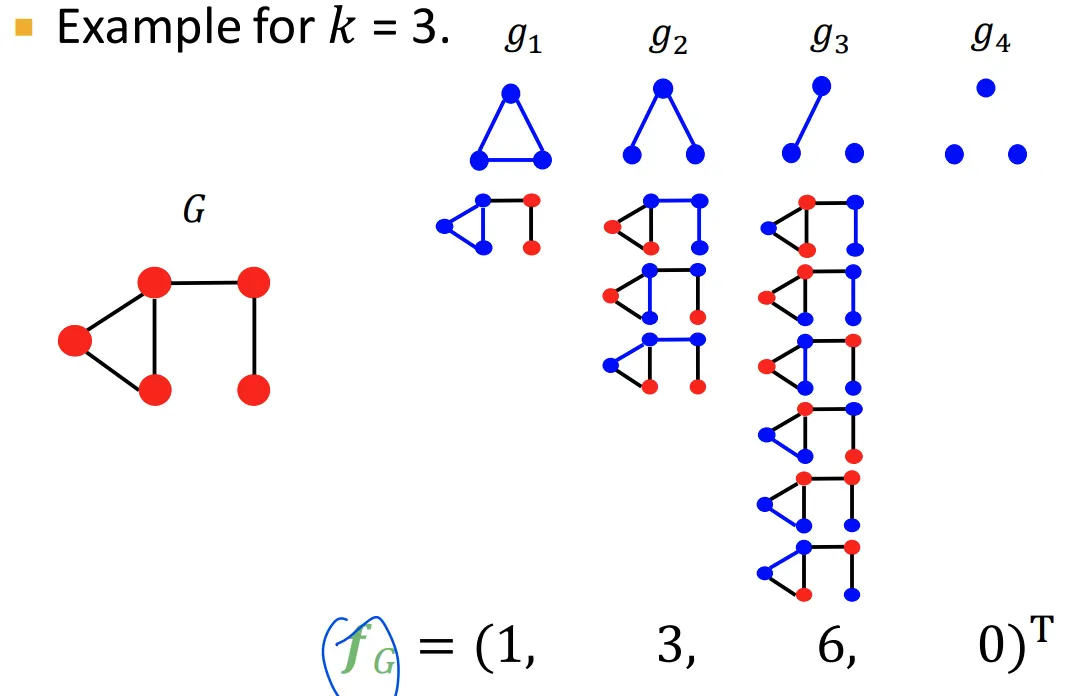
Graphlet kernel
◦
Graph에 있는 graphlet들의 bag-of-words
◦
끊어진 그래프도 관계 없이 카운팅
◦
k=3에 대해서는 4개의 graphlet, k=4에 대해서는 11개의 graphlet이 존재
◦
너무 큰 graph는 graphlet 숫자가 많은데, normalize로 문제 해결
◦
당연히 다 세는 문제이기 때문에 NP-hard한 알고리즘
•
Weisfeiler-Lehman kernel
◦
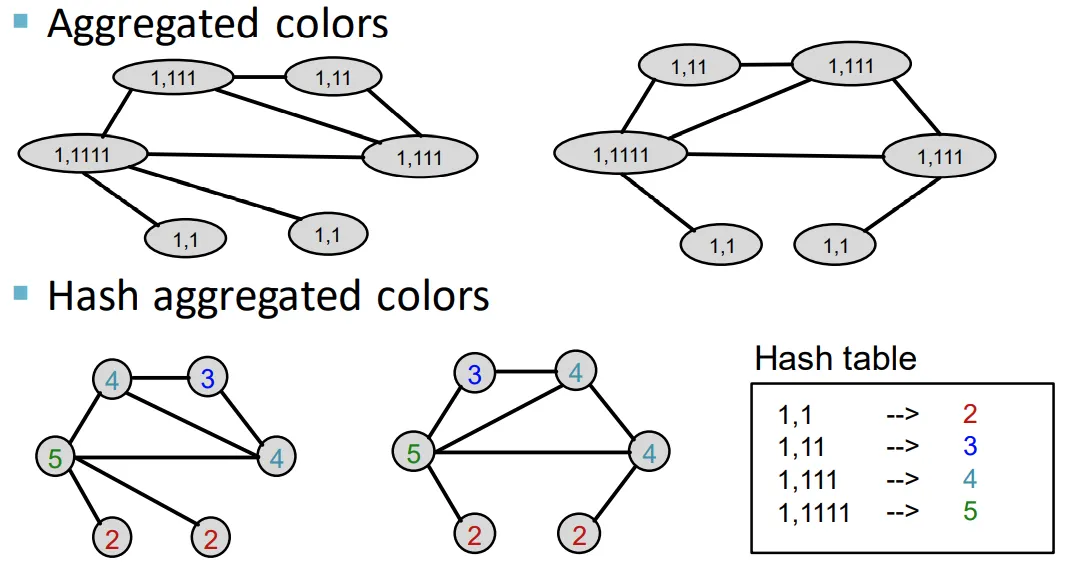
Computational cost를 줄이기 위해 hash 함수활용
◦
K번 알고리즘을 돌리면 k-hop까지 반영 가능
◦
Node의 hash 함수의 결과가 새로운 color가 됨
◦
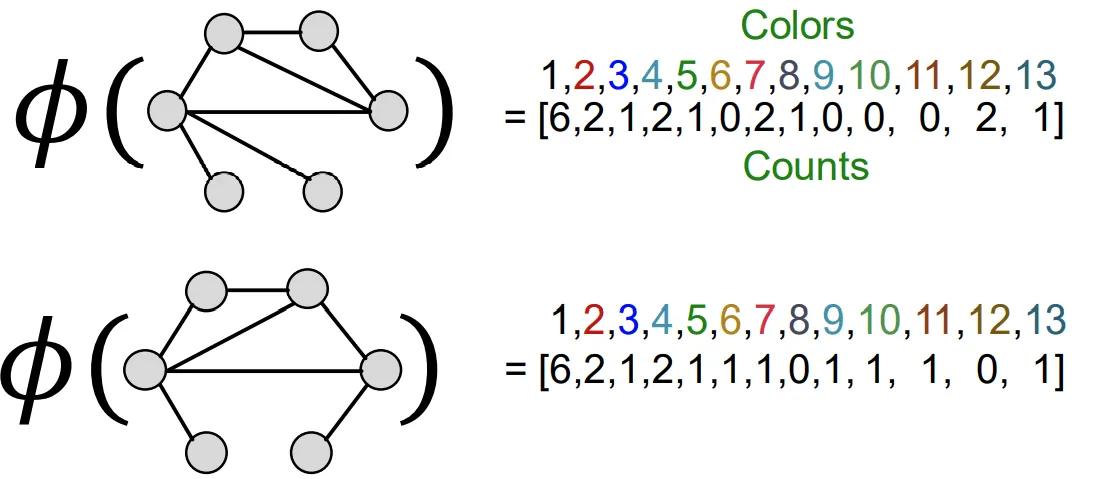
신규 color의 수를 세고, 그것을 벡터화 시킴