Fast Neural Subgraph Matching and Counting
Subgraph를 구별하고 세는 방법들
→ ML을 써서 가능함
순서
•
Subgraphs and Motifs
•
Neural Subgraph Representations
•
Mining Frequent Subgraphs
1. Subgraphs and Motifs
요약
•
subgraph, motif는 graph의 building block으로 쓰인다
•
subgraph의 frequency, significance를 통해 각 graph의 unique characteristics를 구별
•
random graph를 통해 motif들의 z-score를 구할 수 있다.
1.1. Subgraph definition
•
Node-induced subgraph : subgraph node가 target graph node에 포함되고, edge들도 다 포함되는 경우
•
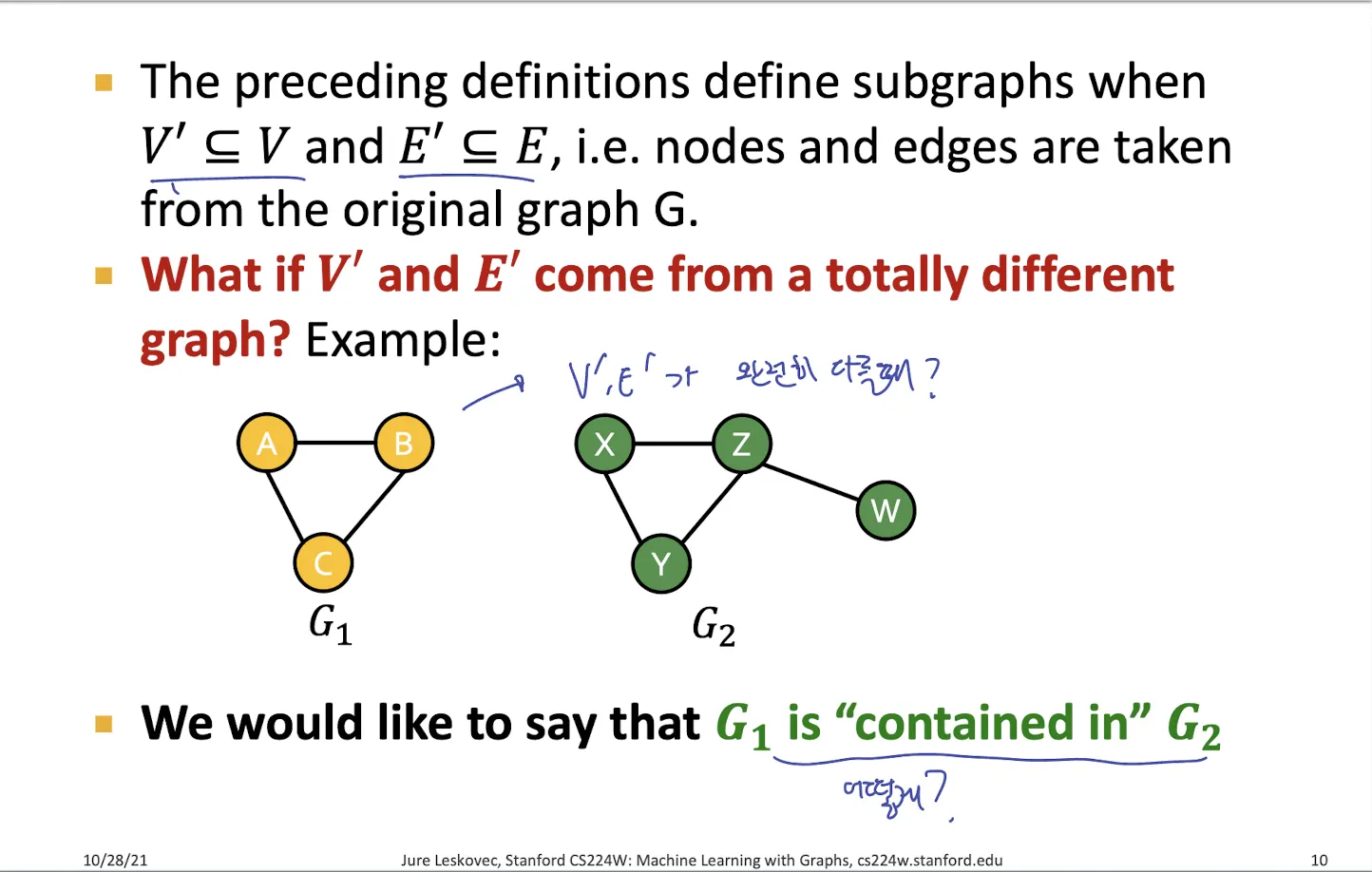
Edge-induced subgraph : subgraph edge가 target graph edge에 포함되고, node들도 다 포함되는 경우
→ 하지만 아래 그림과 같이 subgraph node와 targe graph node의 라벨이 완전히 다를 때 subgraph라 할 수 있는가? 어떻게 하는가?
→ Graph isomorphism
1.2. Graph Isomorphism
•
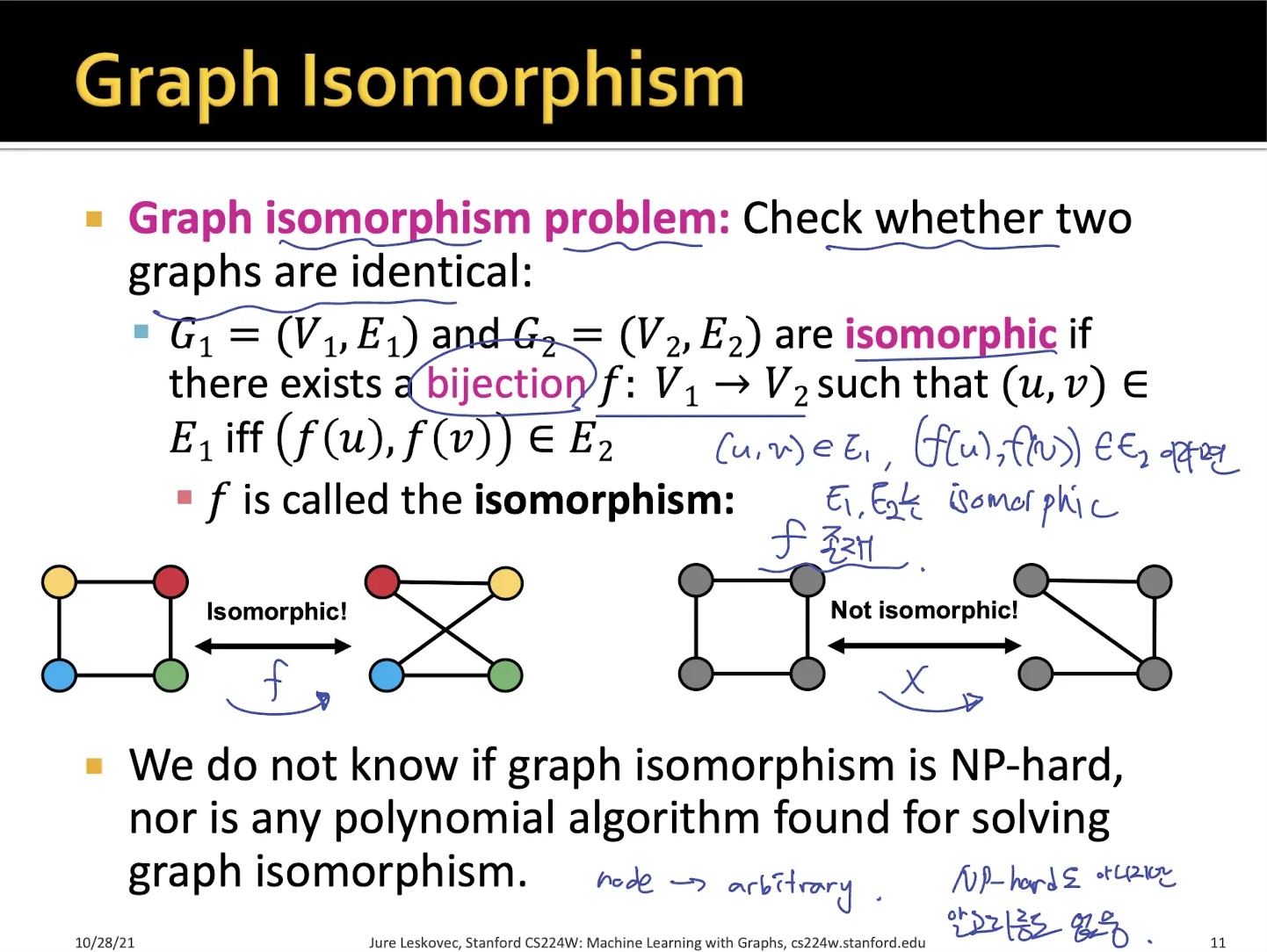
graph가 서로 isomorphic 한지 알아보려면, 두 graph들의 node를 mapping하는 어떤 함수가 존재하면 된다.
•
graph isomorphism은 NP-hard인지 모르고, mapping function을 찾는 알고리즘도 없다.
•
subgraph isomorphism은 subgraph가 isomorphic 한 경우이다.
•
NP-hard에 속함
1.3. Network Motifs
•
Motif란?
•
그래프에서 반복적으로 등장하는 중요한 패턴들
•
Motif가 필요한 이유는 graph의 성격을 해석할 수 있기 때문이다.
•
feed-forward loop, parallel loop, single-input modules 등 해당 환경에서 주로 나타나는 motif들이 있다.
→ motif가 얼마나 자주나타나는지 (frequency), 얼마나 중요한지 (significant or z-score)를 측정한다
1.4. Subgraph Frequency
•
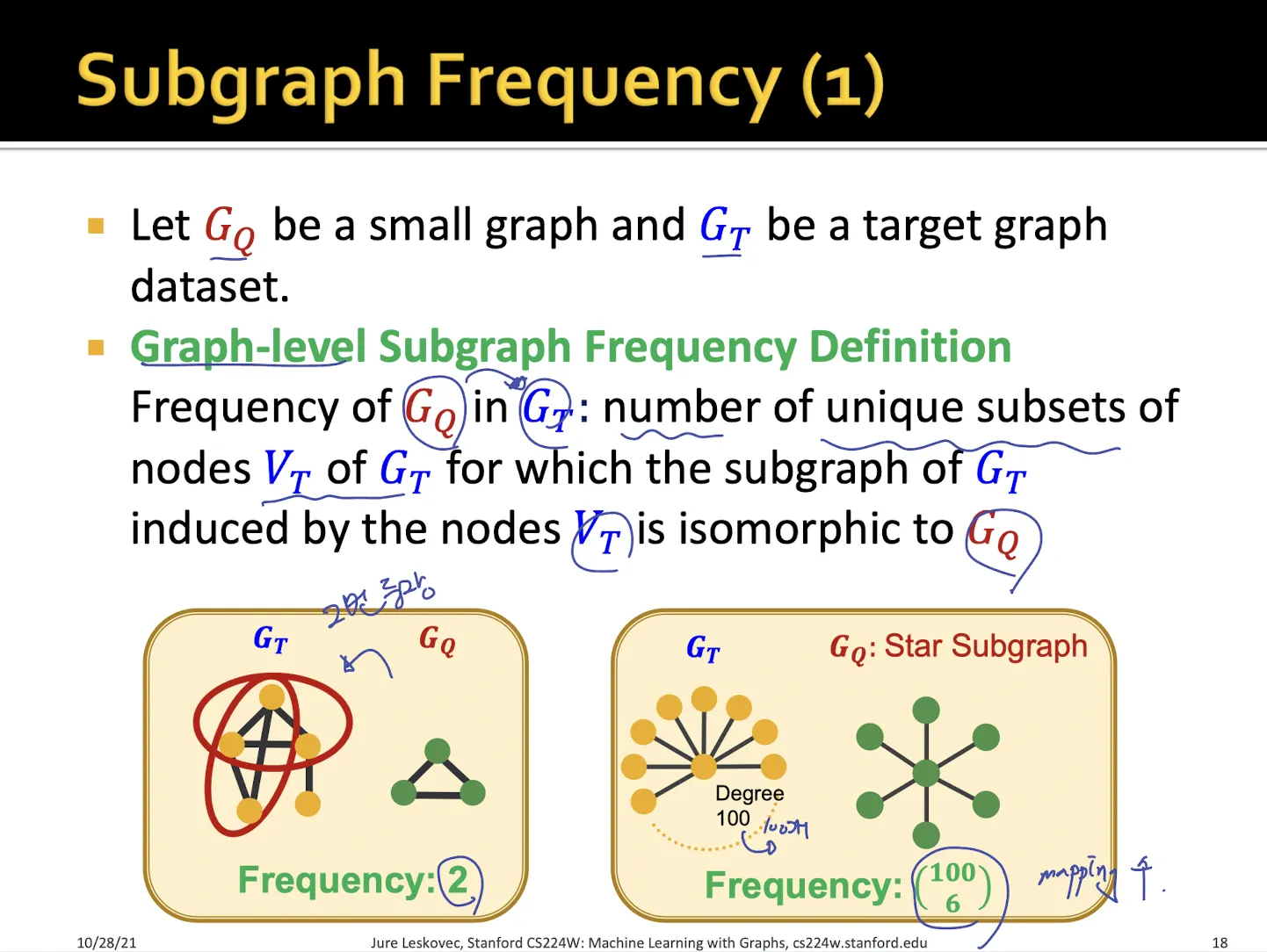
Frequency를 측정하는 방법은 graph-level 과 node-level로 나눌 수 있다.
•
Graph-level에서는 모든 node를 abitrary라 생각하고 subgraph의 개수를 센다
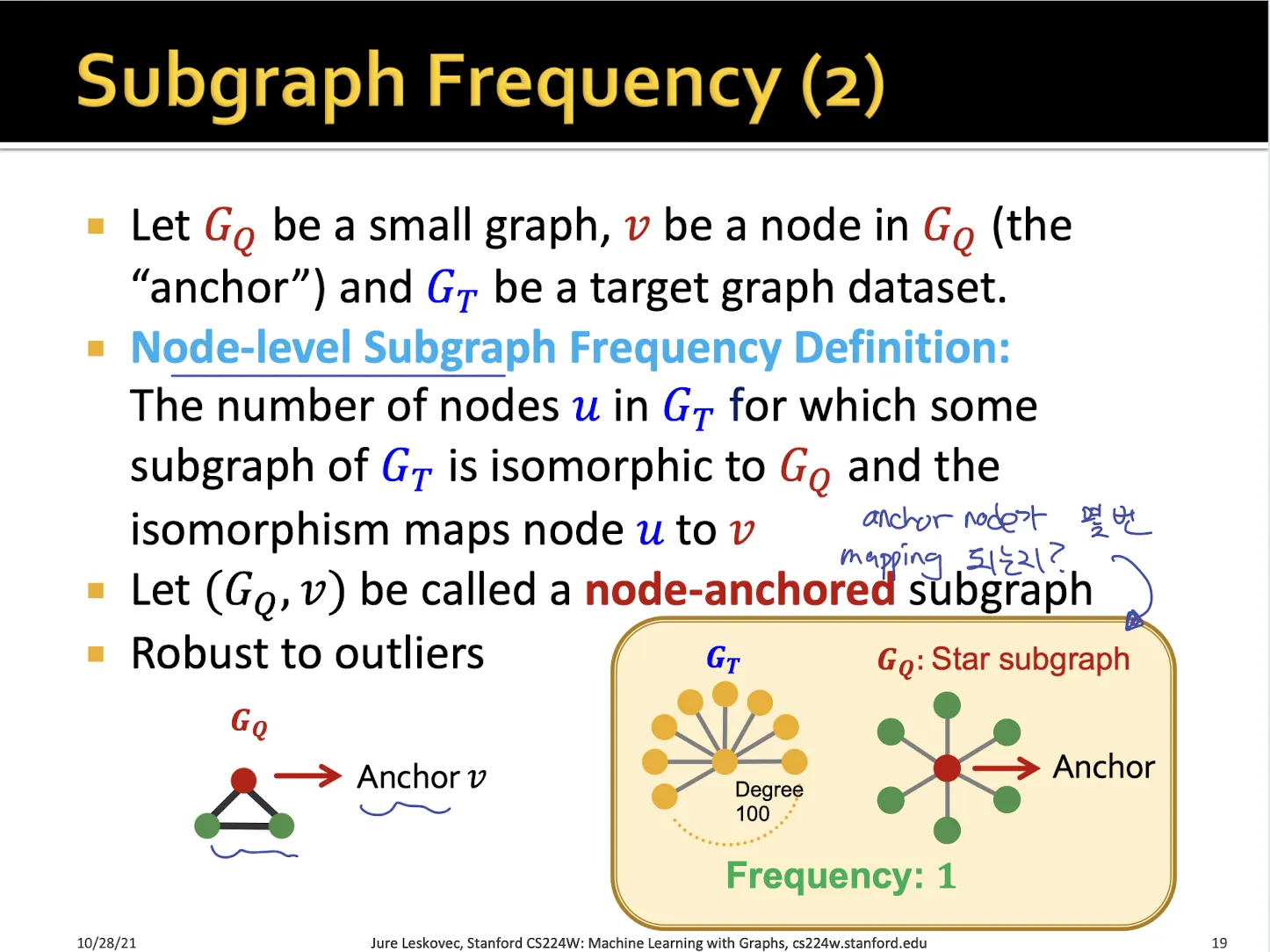
•
Node-level에서는 anchor node가 그래프에서 몇 번 등장하는지 센다
1.5. Motif Significance
•
Significance를 측정하는 방식
•
해당 motif가 real network에서 많이 등장하고 random network에서는 많이 등장하지 않는다면, 해당 motif는 real network에서 중요한 subgraph일 것이다.
→ 어떻게 random graph를 만드는가?
→ 2가지 방법
•
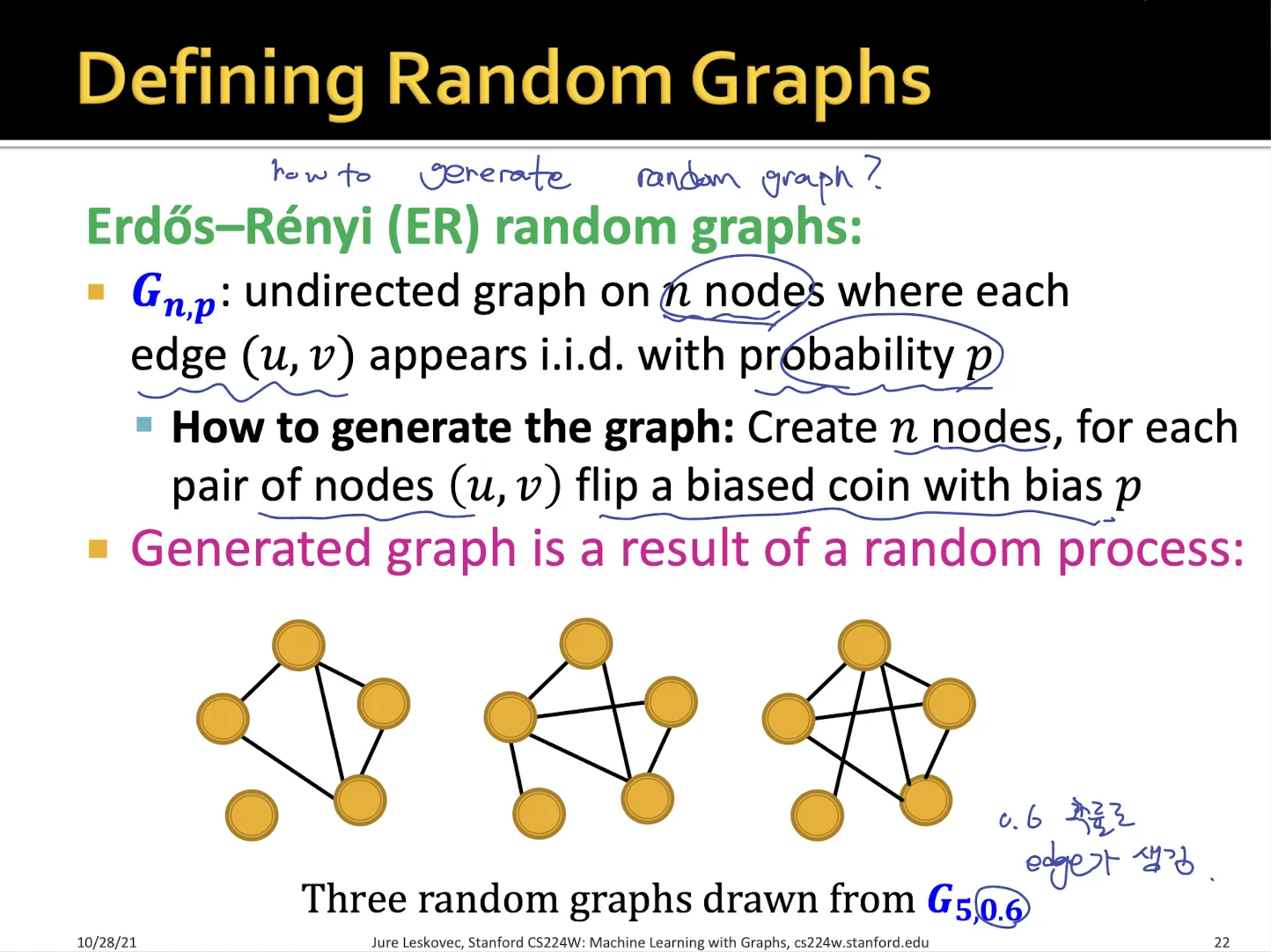
ER random graph
•
몇 개의 node가 graph에 들어가있는지 설정, 특정 확률로 node끼리의 edge가 존재
•
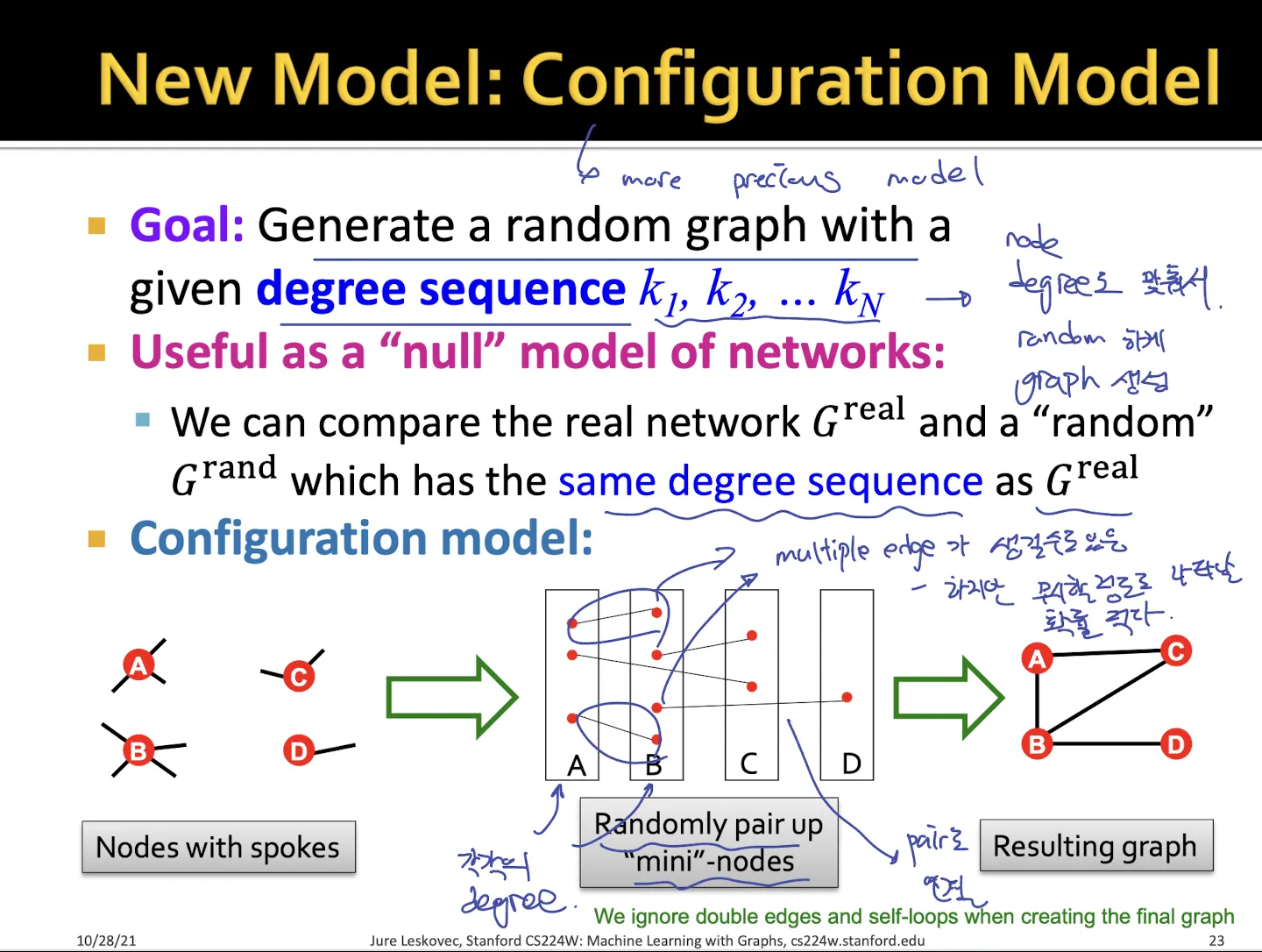
Configuration Model
•
각 node들의 degree까지 미리 정해둠
•
pair로 degree만큼 생성된 각 node들을 무작위로 연결
→ 두 node를 연결하는 edge가 1개가 아니라 여러개인 multiple edge가 생길 수도 있지만 확률이 매우 낮아서 괜찮다고 함
1.6. Motif Significance Measure
•
위에서 처럼 random 하게 graph를 만들어서 motif가 몇 개인지 카운팅
→ 수학적으로 어떻게 significance를 나타낼 수 있는가?
•
각각의 motif에 대해서 를 계산할 수 있다.
•
는 real network의 motif가 random network의 motif의 개수와 얼만큼의 차이가 나는지를 나타낸 것이다.
•
z-score를 통해 network significance profile 를 구할 수 있다.
•
는 각 motif의 z-score를 normalize한 것이다.
•
network의 종류에 따라서 significance profile이 달라지게 된다.
•
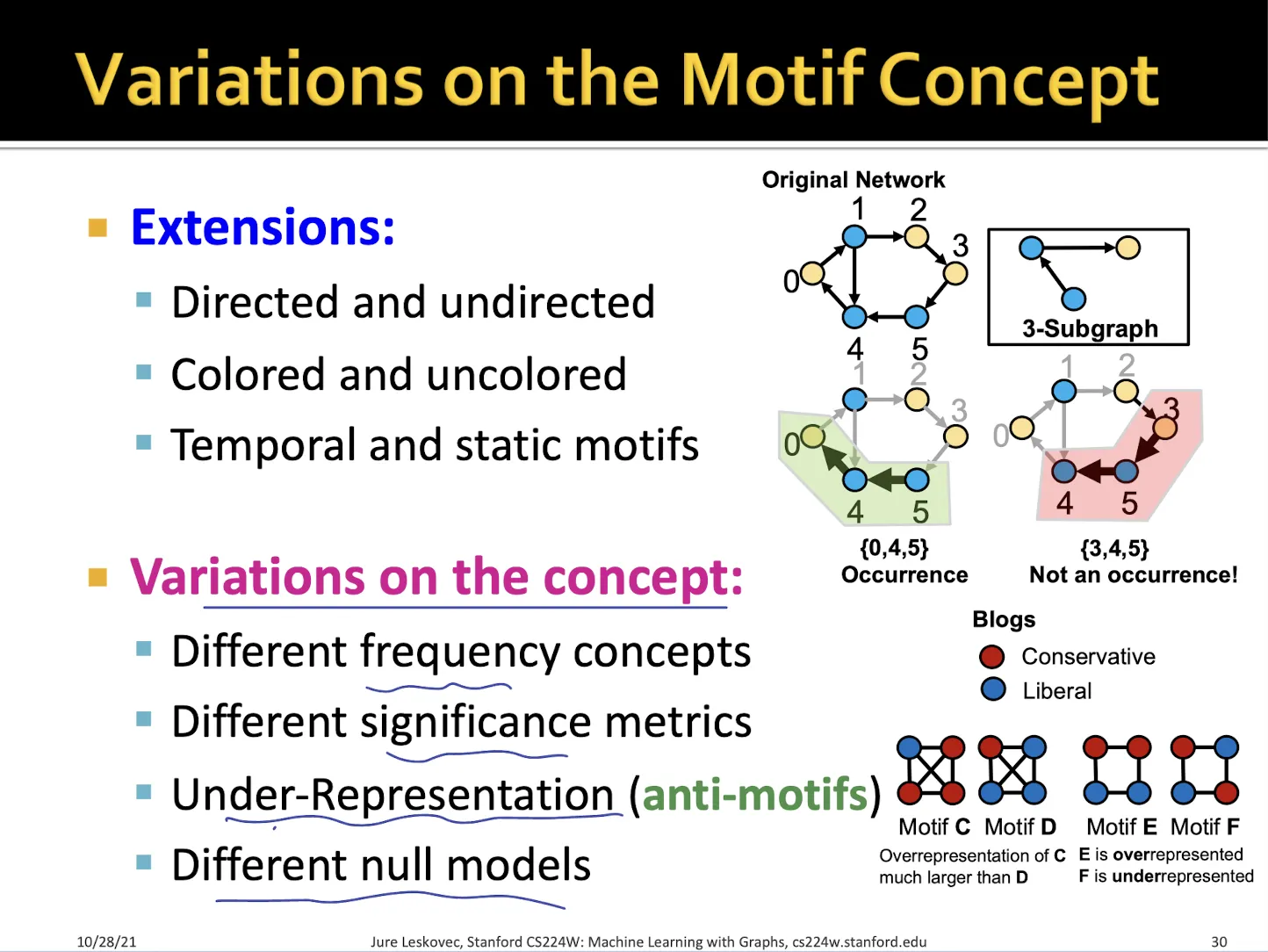
Z score가 커질수록 over representation으로 random한 network에 비해 해당 motif가 상당히 많이 등장한 것이다.
•
Z score가 작아질수록 under representation으로 random한 network에 비해 해당 motif가 등장하지 않은 것이다.
→ over representation 과 under representation 모두 network에서 중요한 의미를 가진다.
•
social network에서 6번 motif가 상대적으로 작은 z-score를 가지고 13번 motif가 상대적으로 큰 z-score를 가짐을 볼 수 있다.
Summary
•
z-score로 motif의 significance를 파악할 수 있다
2. Neural Subgraph Matching
subgraph matching을 ML task로 만들어서 푸는 방법 소개
2.1. Task Define
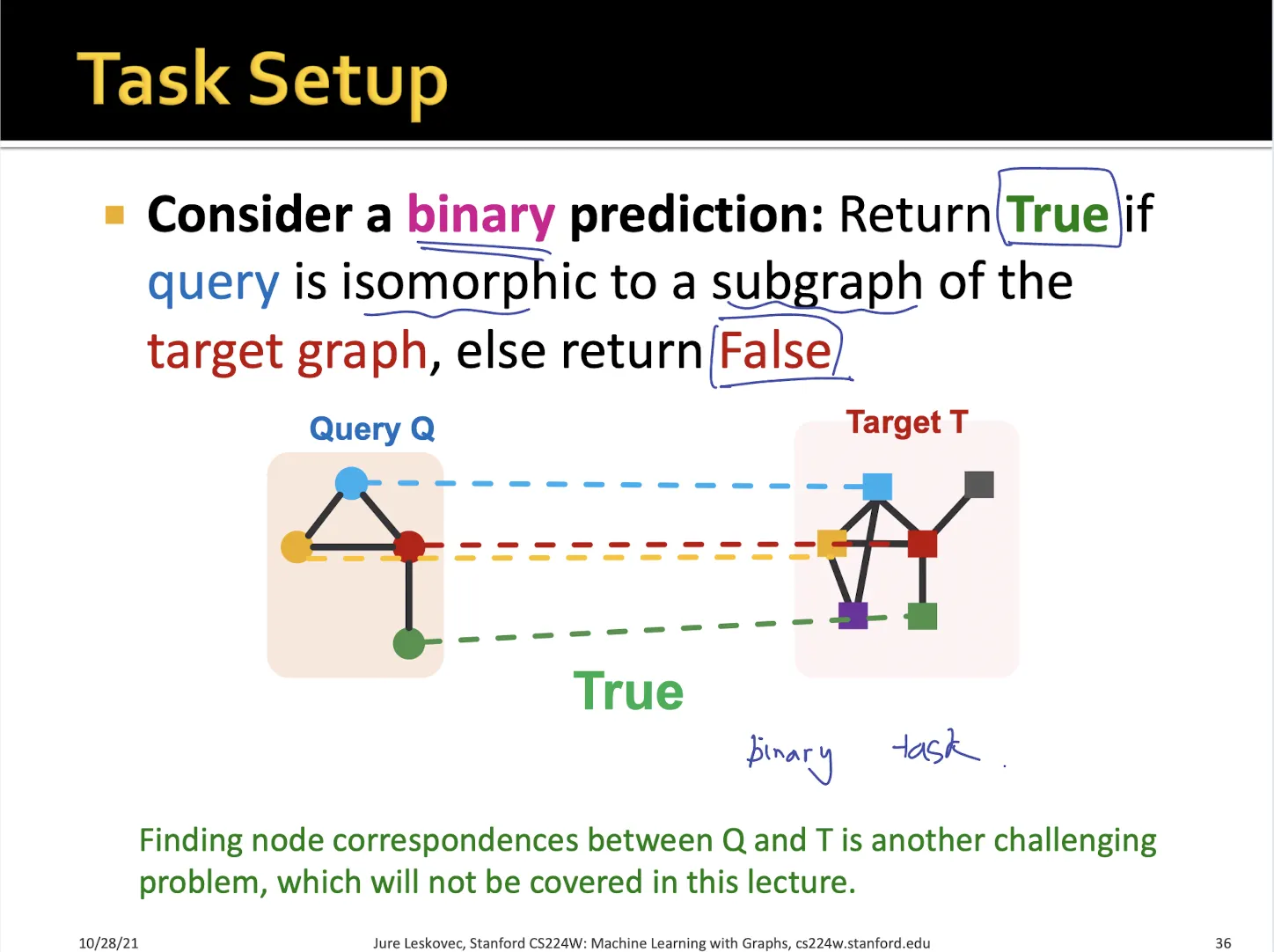
•
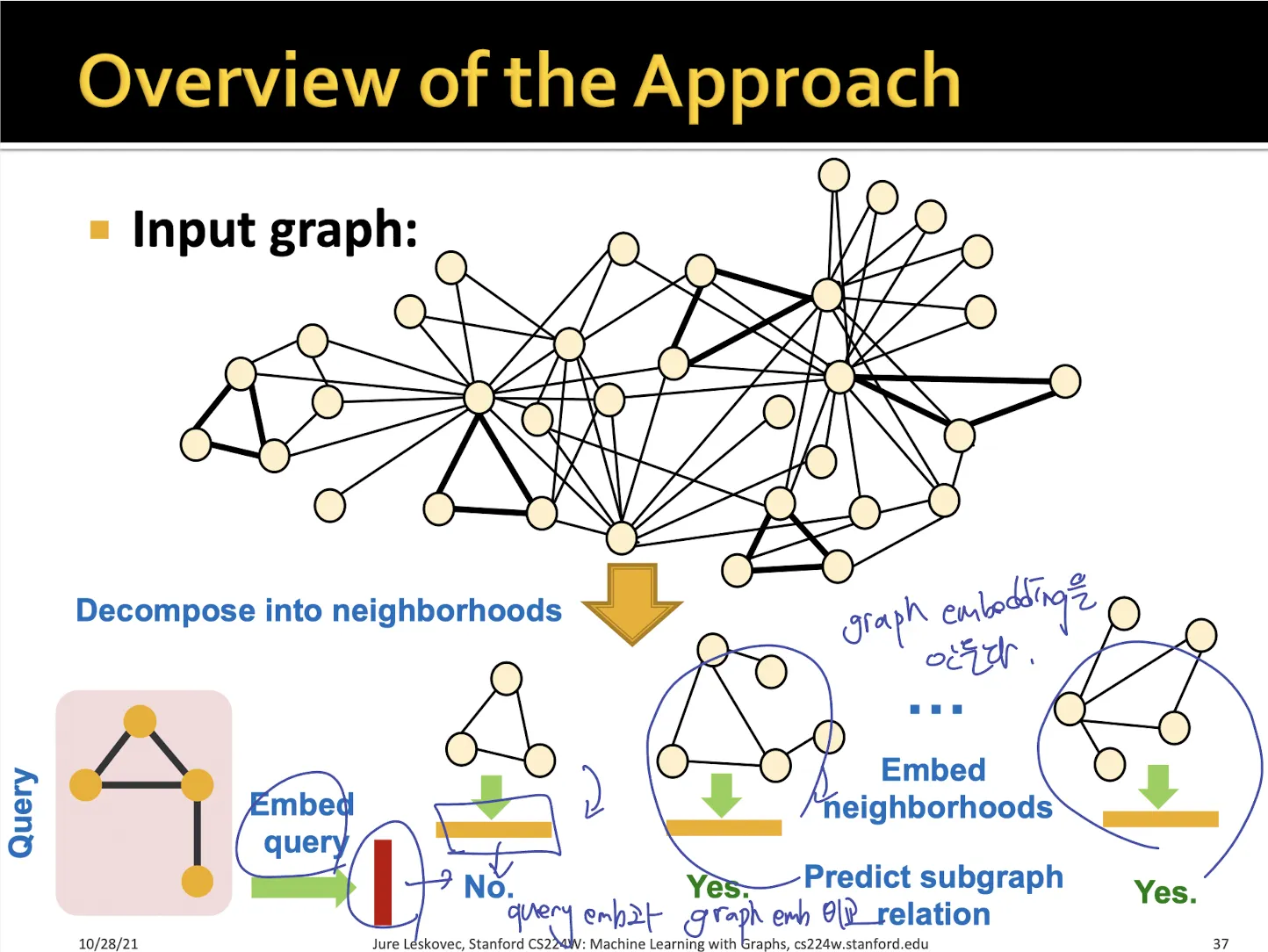
query graph가 target graph에 속하는지 binary prediction task로 생각할 수 있다.
•
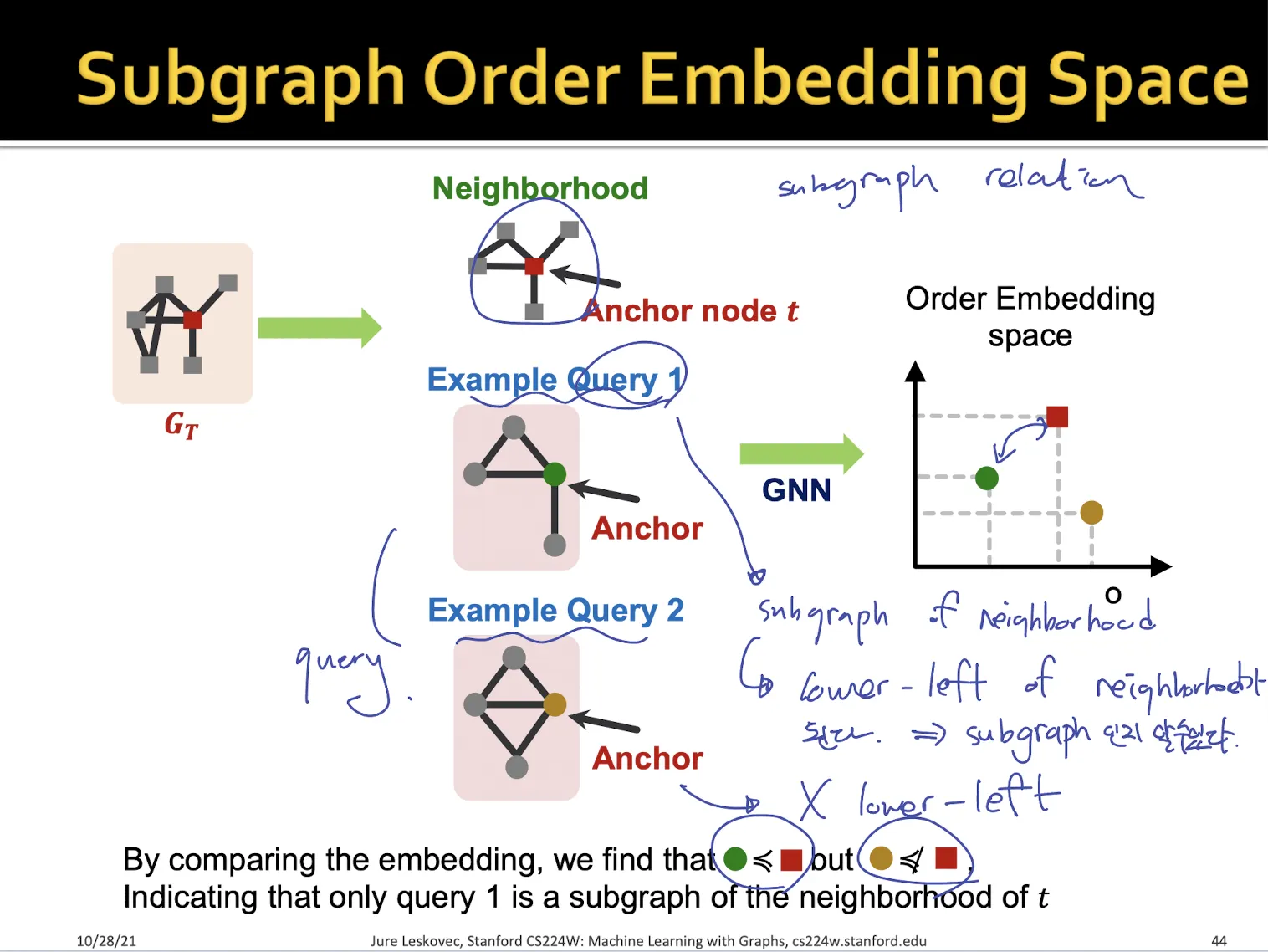
query graph의 embedding과 target graph 에서 sampling하여 neighbor hood embedding을 구해서 비교한다.
2.2. Neural Architecture
•
subgraph인지 판단하는 방법으로 2가지 neural architecture가 있다
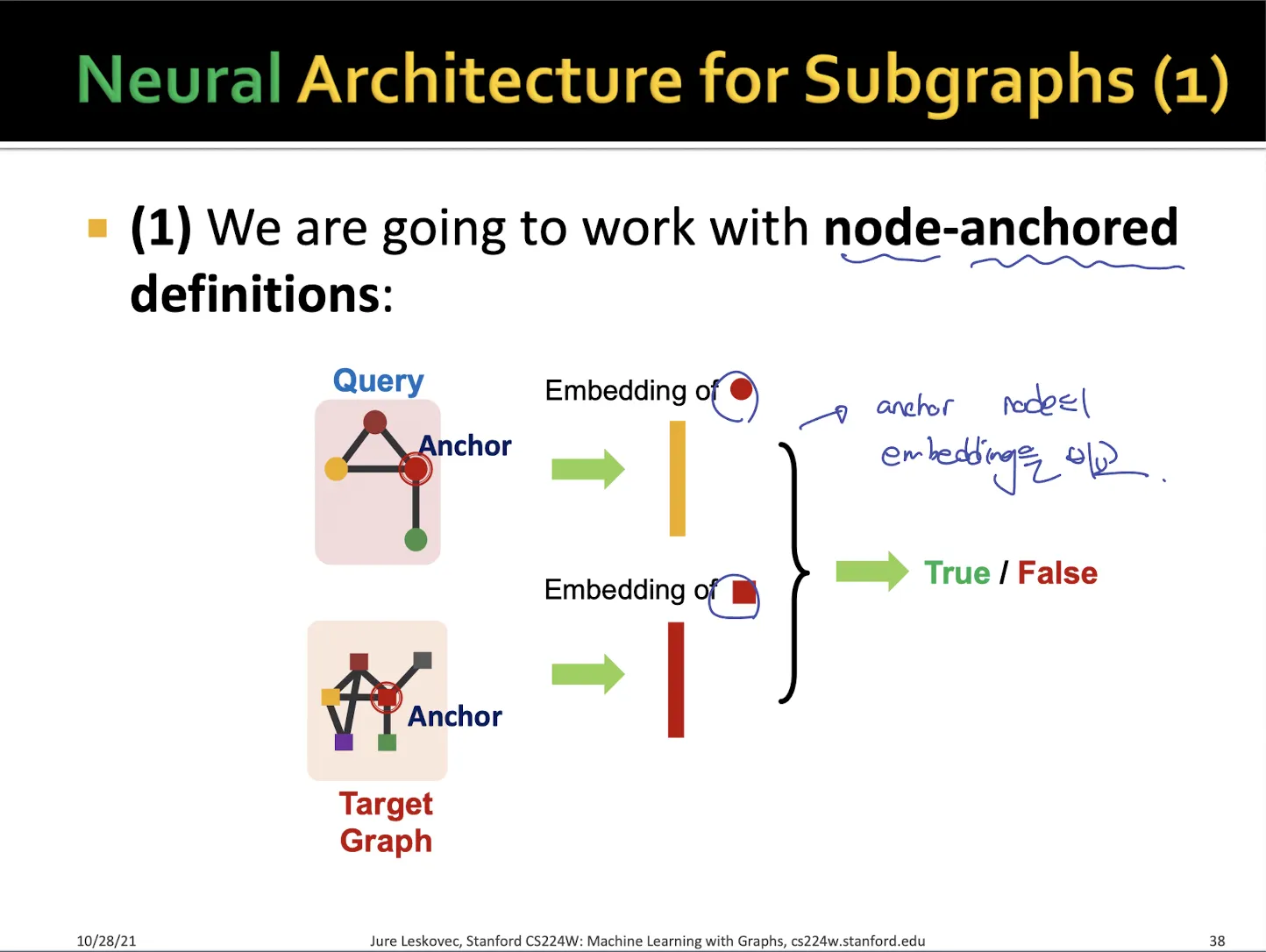
•
anchor node의 embedding을 비교하는 방법
•
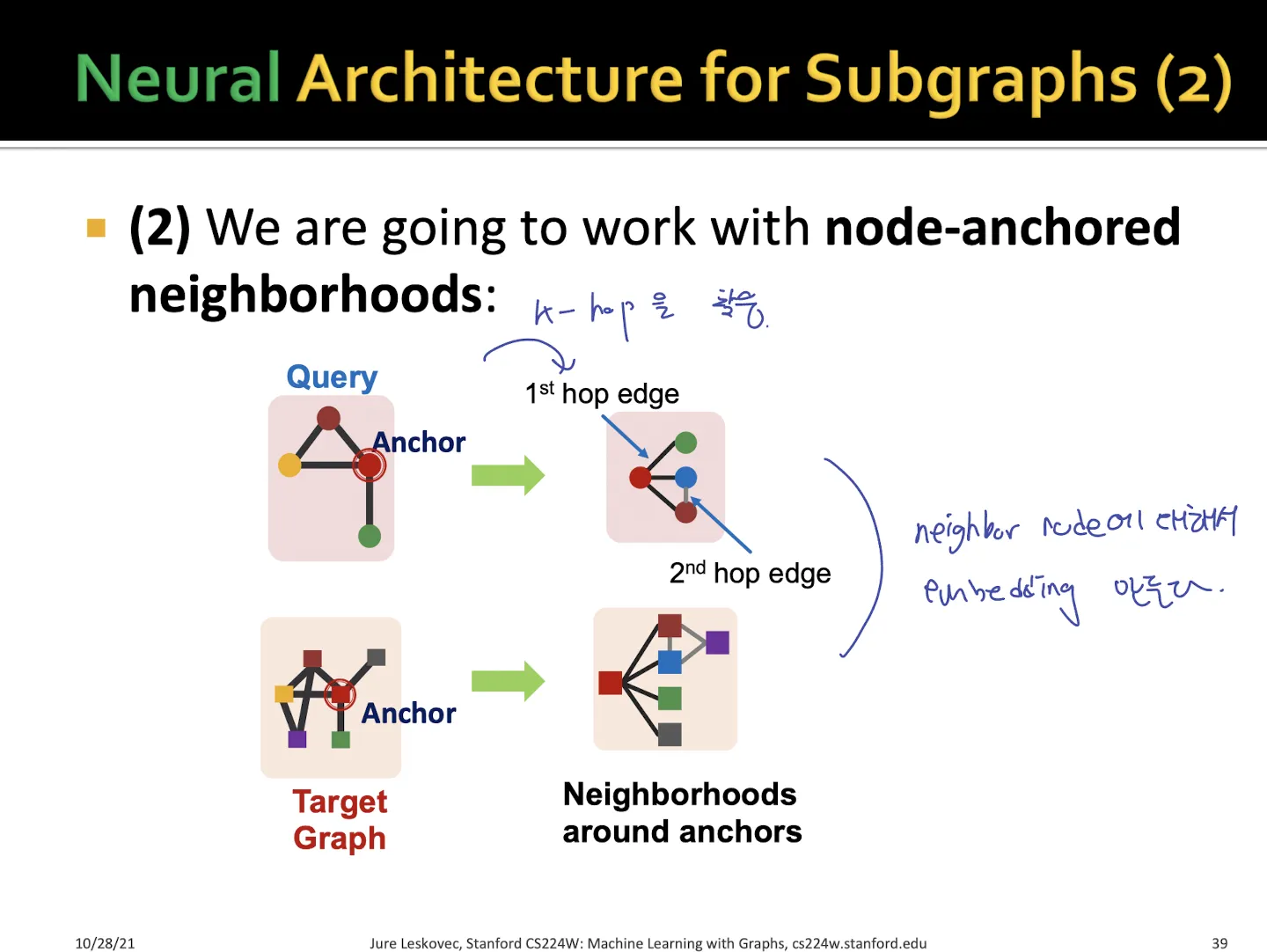
anchor node의 neighbor 들을 embedding으로 만들어서 비교하는 방법
•
target graph 에서 각 anchor에 대해서 k-hop neighborhood embedding을 뽑아낸다.
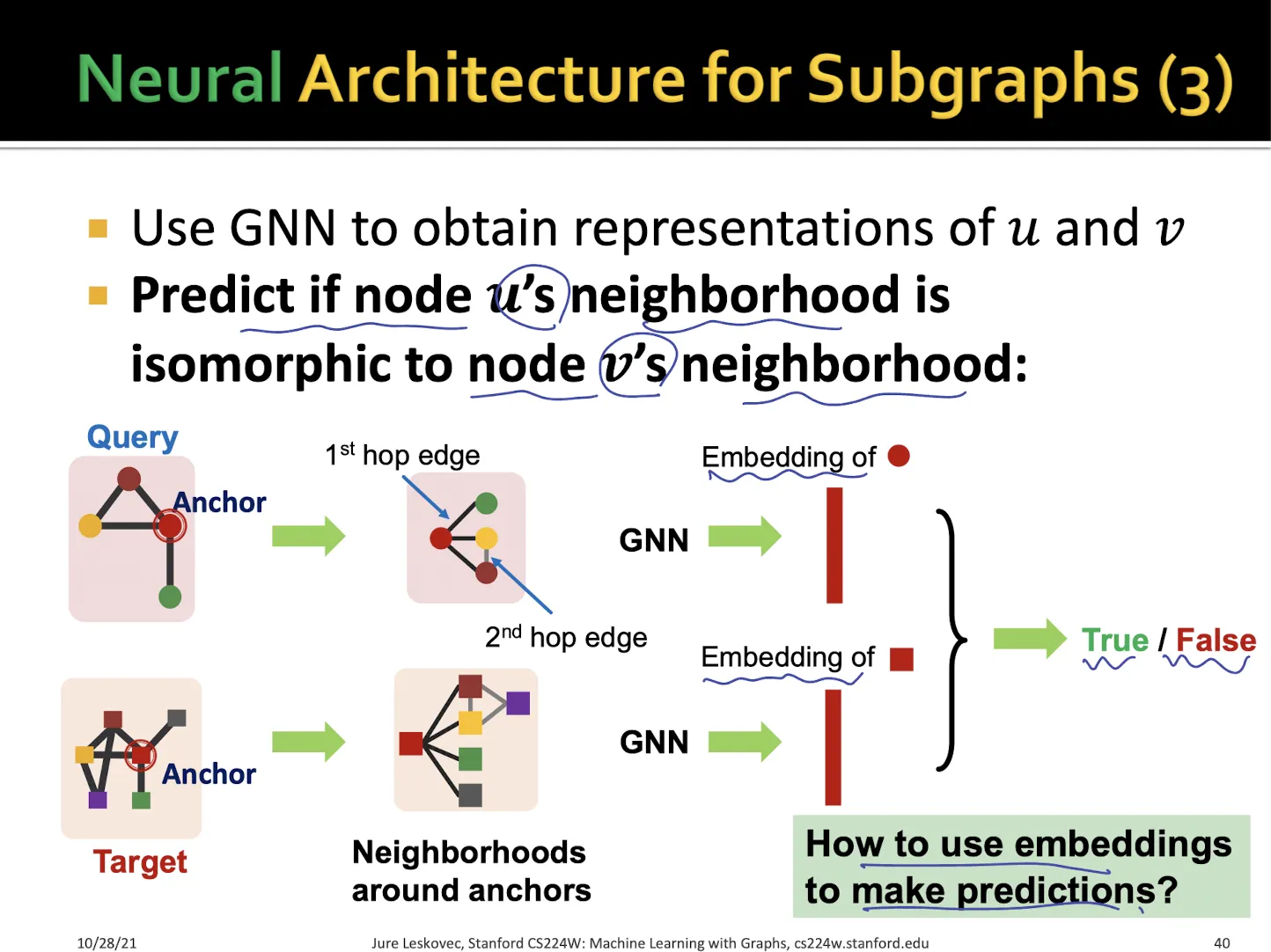
•
마찬가지 방법으로 에 대해서도 neighborhood embedding을 구한다.
→ embedding은 구했지만 어떻게 가 의 subgraph인지 알 수 있는가??
→ order embedding space
2.3. Order Embedding Space
•
embedding space의 모든 차원에 대해서 값이 작을 때 lower-left라고 한다.
•
모든 dimension이 non-negative 하다고 가정
•
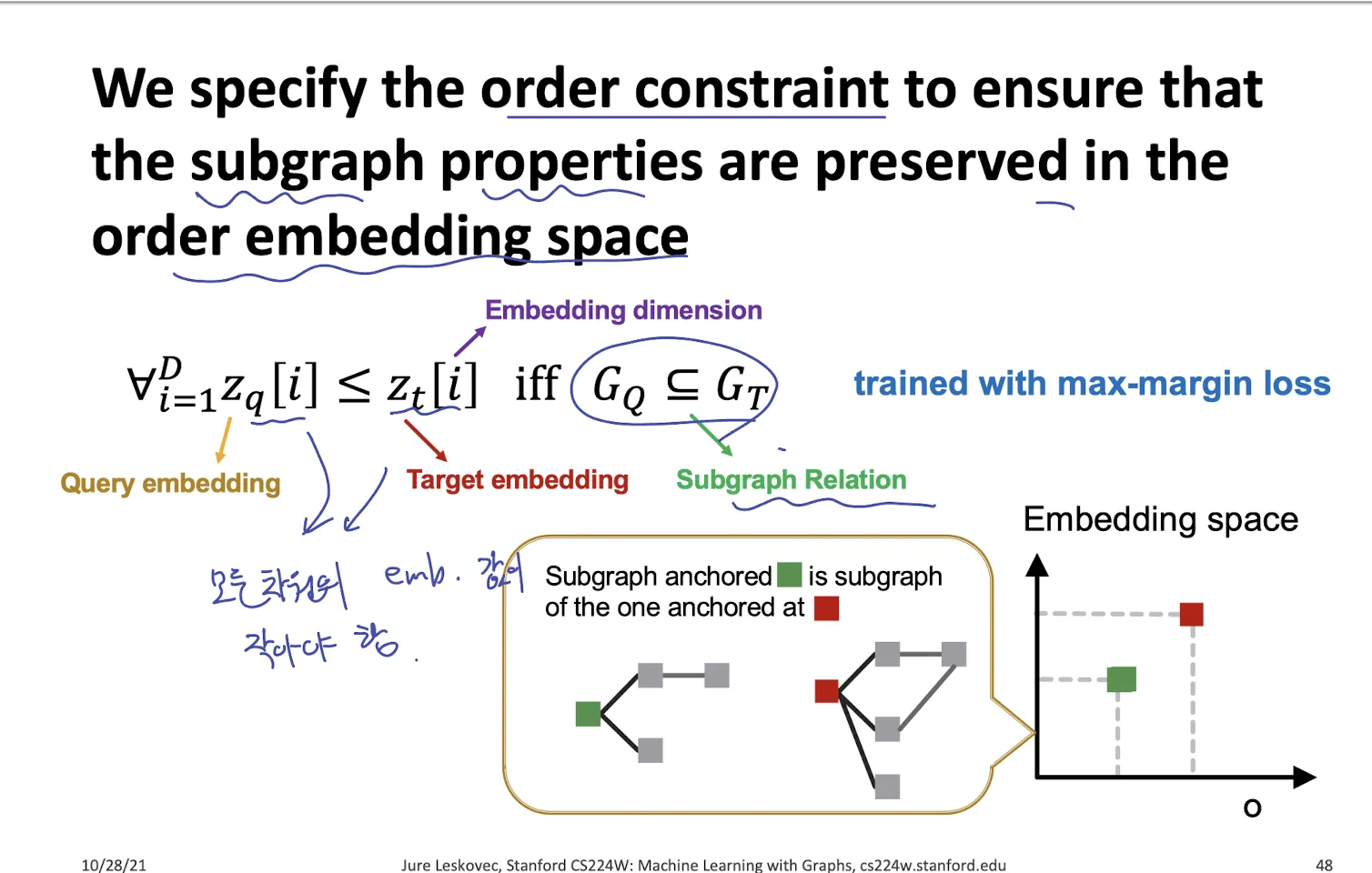
query graph의 node embedding에 대해서 target graph의 node embedding 보다 lower-left라면 subgraph라 말할 수 있도록 모델링
→ 어떻게 이렇게 학습할 수 있는지는 그 다음 슬라이드에서 설명
•
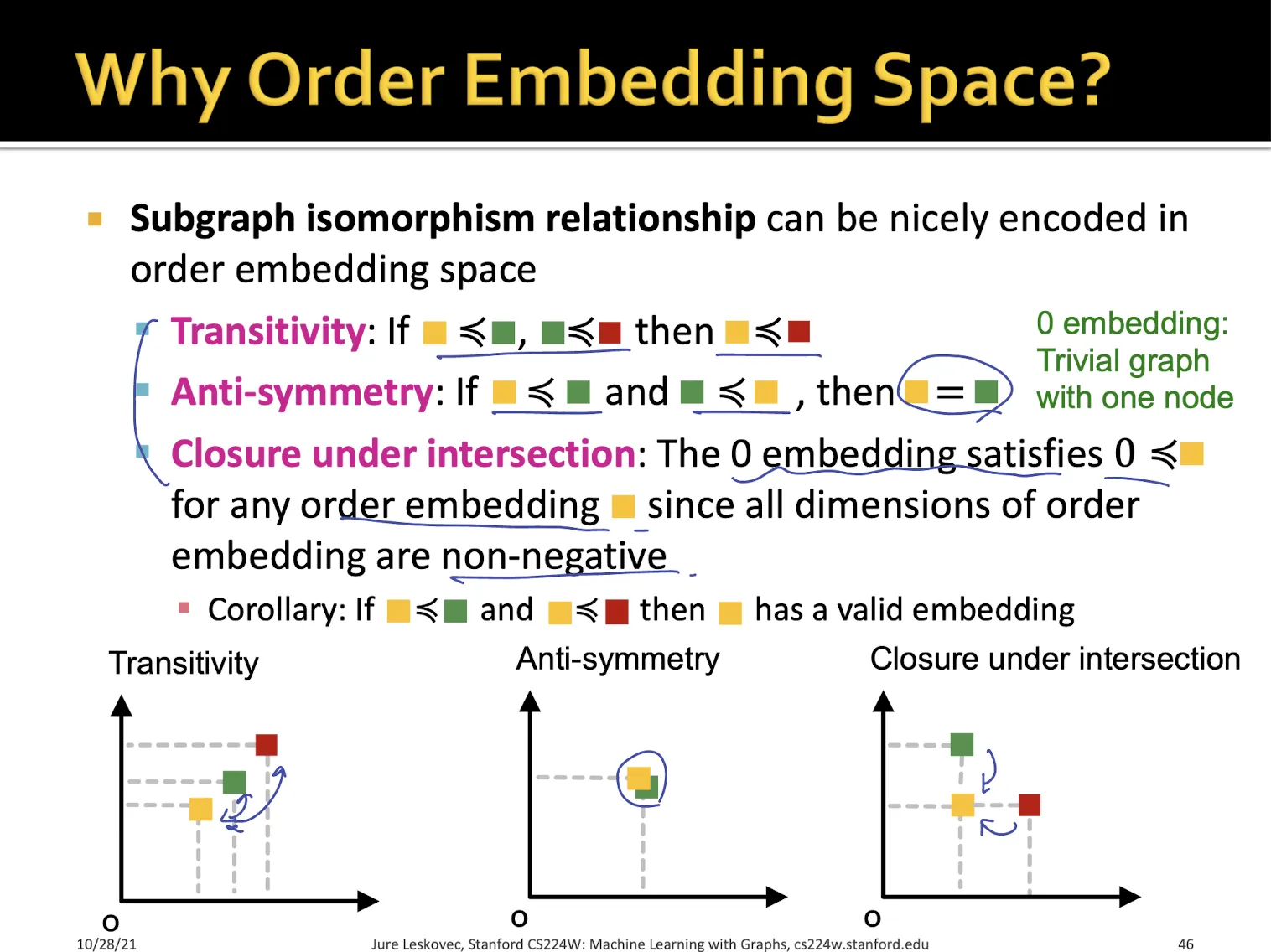
order embedding space를 사용하는 이유
•
여러가지 특징이 있음
2.4. Loss Function
•
lower-left 이면 subgraph가 되도록 학습하고 싶음
•
Max-margin loss
•
lower-left라면 E 가 0이고, 만약 lower-left가 아니라면 E > 0 값을 가진다.
→ lower-left에 가까워질수록 E는 0에 가까워진다.
→ subgraph에 대해서 E를 loss function 처럼 생각한다면, subgraph인지 판단하는 모델을 학습할 수 있지 않을까?
•
가 의 subgraph의 관계일 때 이 되도록 order embedding을 학습했다면, 이면 subgraph, 이면 subgraph가 아니라고 예측할 수 있다.
2.5. Training
•
training을 하는 방법?
•
positive example - query graph와 target graph가 subgraph 관계라면 를 최소화
•
negative example - subgraph 관계가 아니라면? 를 최소화
→ 의 값이 가 되도록 학습하는 것
→ 는 0보다 큰 hyperparameter
•
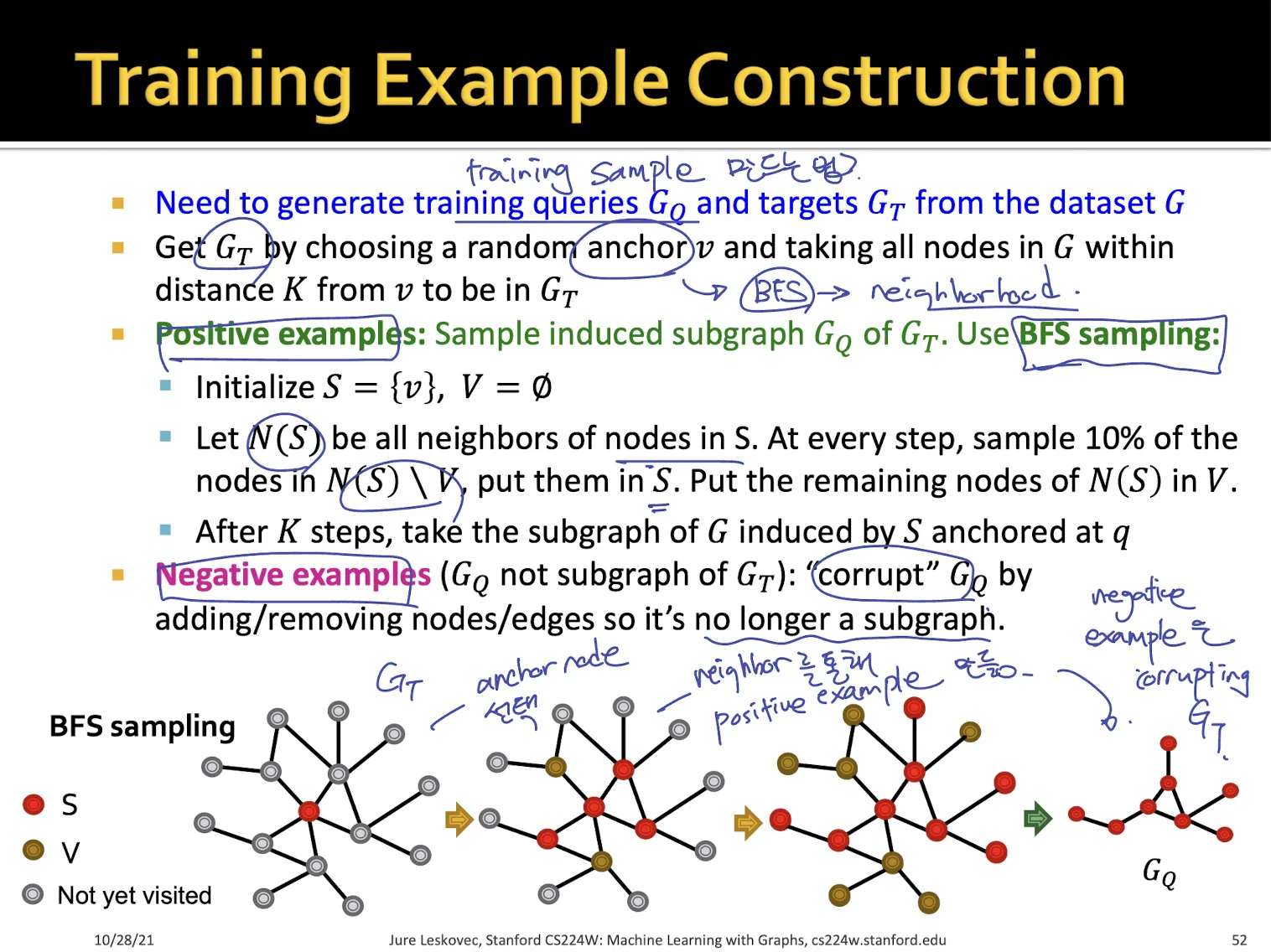
training set은 target graph에서 anchor를 뽑아 neighbor node들을 sampling하여 만든다.
•
negative example의 경우 위에서 뽑은 positive example graph에서 edge나 node를 날려서 만든다.
•
training sample 수?
◦
매 iteration에서 새로운 training pair를 뽑아낸다 - overfitting 방지
•
depth?
◦
3~5 depth 사용
Summary
•
NP-hard 문제를 ML로 풀 수 있다
→ 하지만 ML 이기 때문에 100% 확신하는 결과는 아니라고 생각
3. Finding Frequent Subgraphs
Subgraph의 frequency를 세는 방법?
•
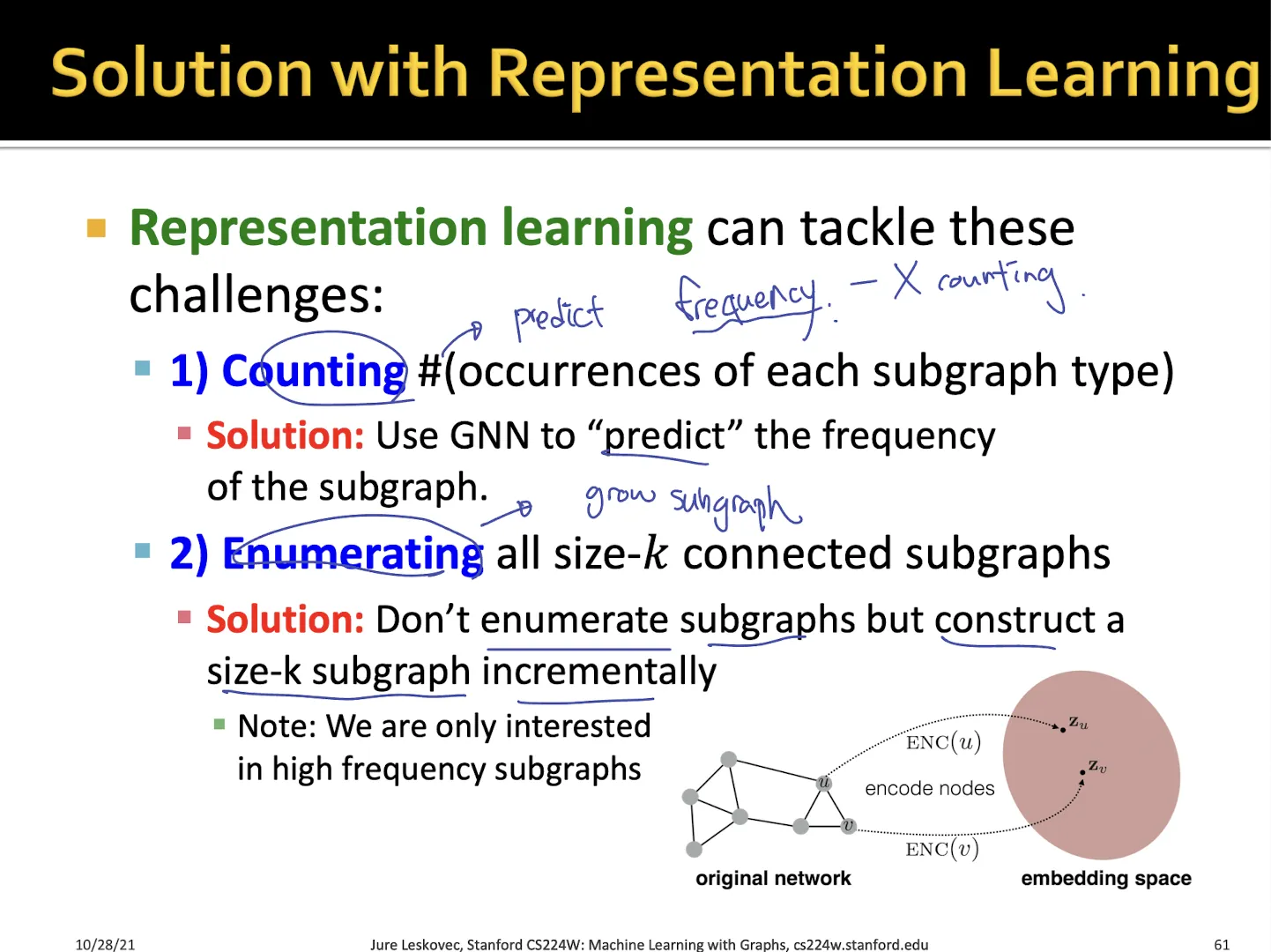
subgraph frequency를 counting하는 것이 아니라 predict 해야함
•
size-k 의 가능한 subgraph들을 모두 계산해야 함, k의 값을 증가시킬 수 있는가
•
size-k인 graph 중 target graph에서 가장 많이 나타난 graph를 찾는 것
3.1. SPMiner
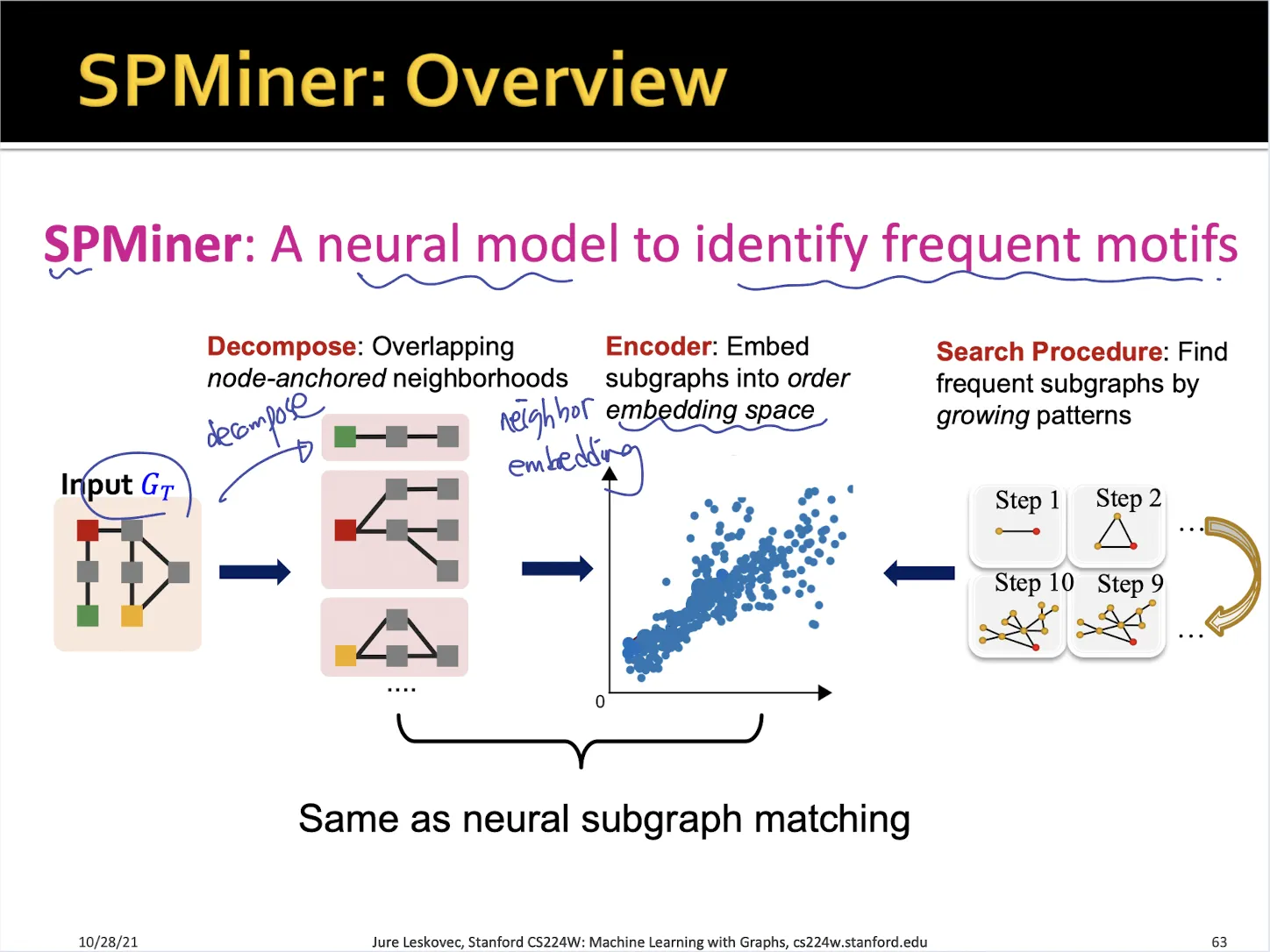
•
target graph에 대해서 여러개의 sample graph로 쪼갠뒤 graph embedding을 구한다
•
각 size 별로 frequent한 subgraph를 greedy algorithm으로 구한다
→ brute force algorithm으로 세는 것보다 훨씬 빠르고 효율적이다
3.2. Motif frequency estimation
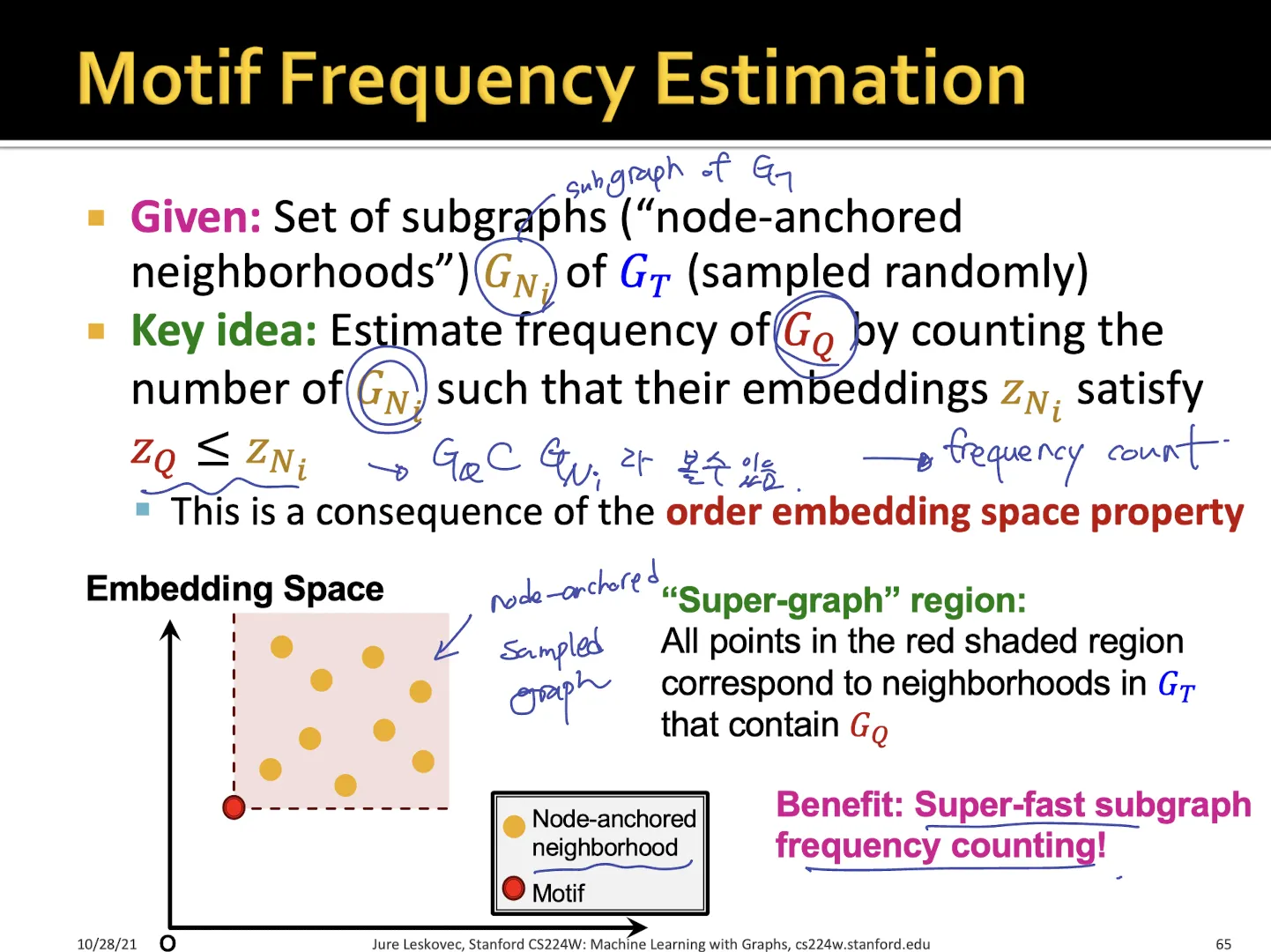
•
target graph의 sampling된 subgraph에 대해서 motif가 lower-left 라면?
•
motif는 subgraph 들에 속하는 것으로 볼 수 있다.
→ sampling된 subgraph에 motif에 속해있는 것이므로 motif의 target graph에 대한 frequency를 구하는 것과 같다
3.3. SPMiner Search Procedure
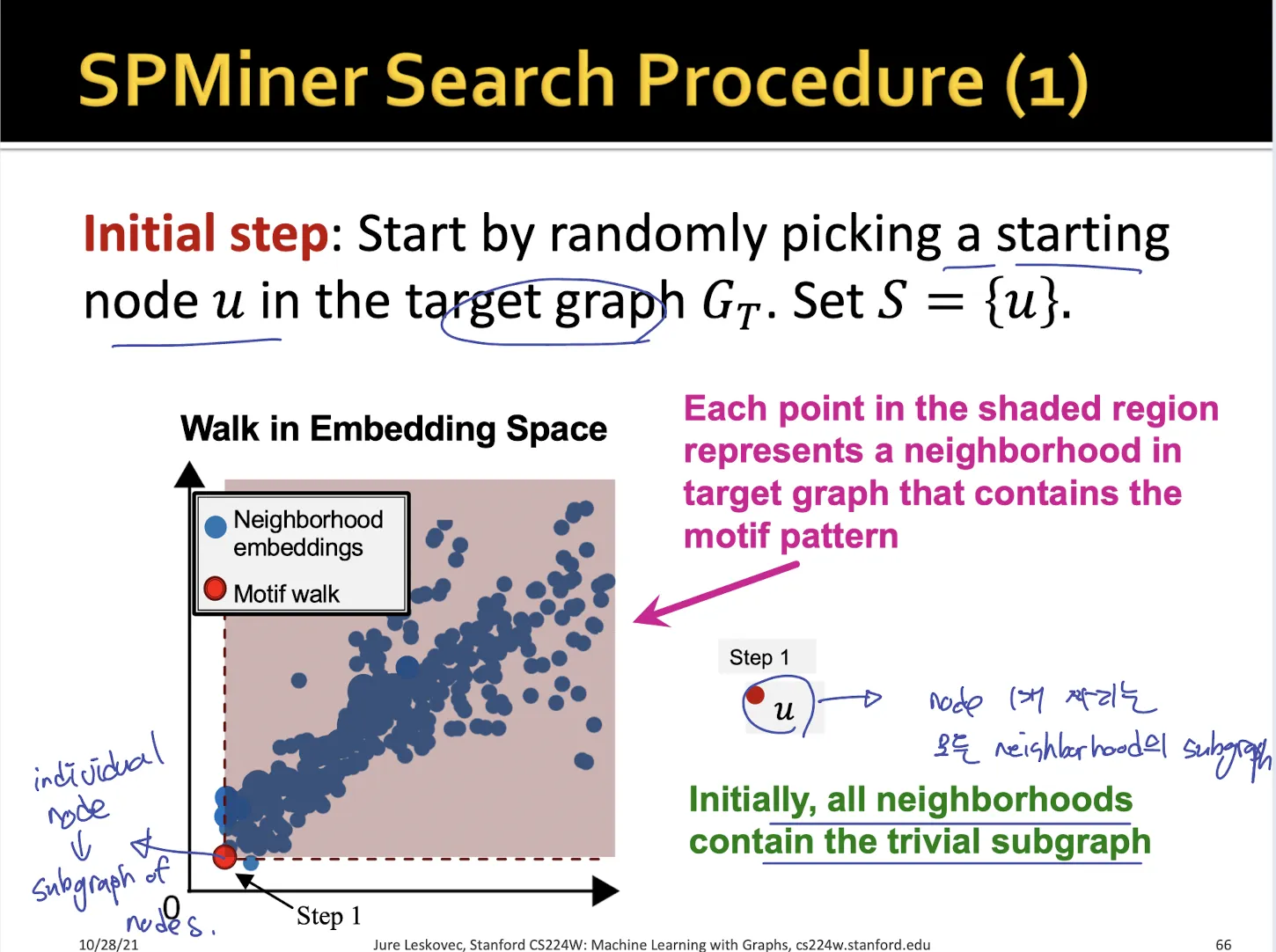
•
처음에는 size 1 node graph로 시작한다
•
모든 sample subgraph (neighborhoods) 에 대해서 포함되어 있다
•
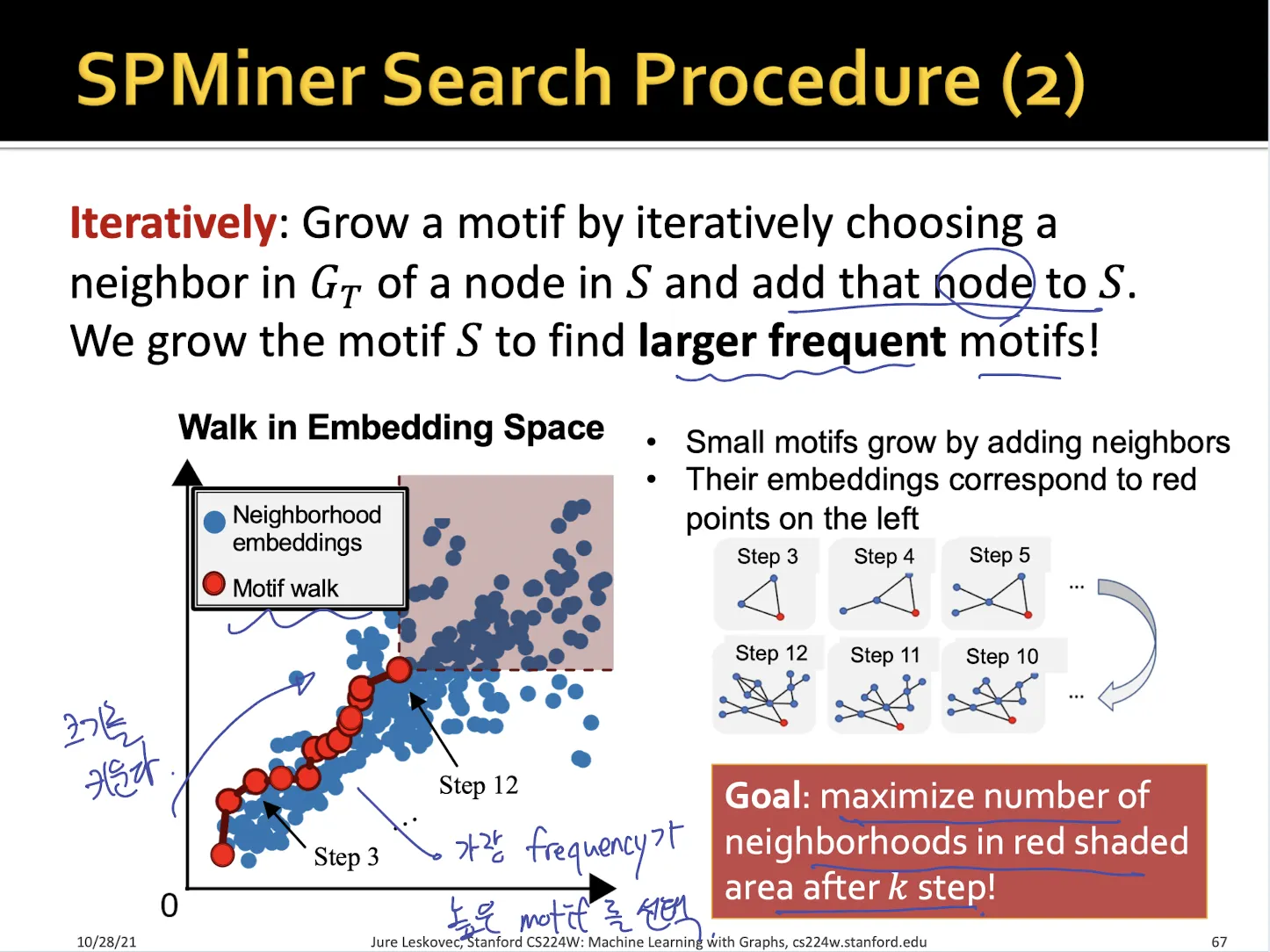
size 를 증가시키면서 shaded region을 최대로 하는 motif를 찾는다. → 매 step에서 node를 1개씩 추가
•
shaded region은 해당 motif가 포함되어 있는 neighborhoods 들의 영역으로 이 크기가 클수록 motif의 frequency가 높다는 것이다.
•
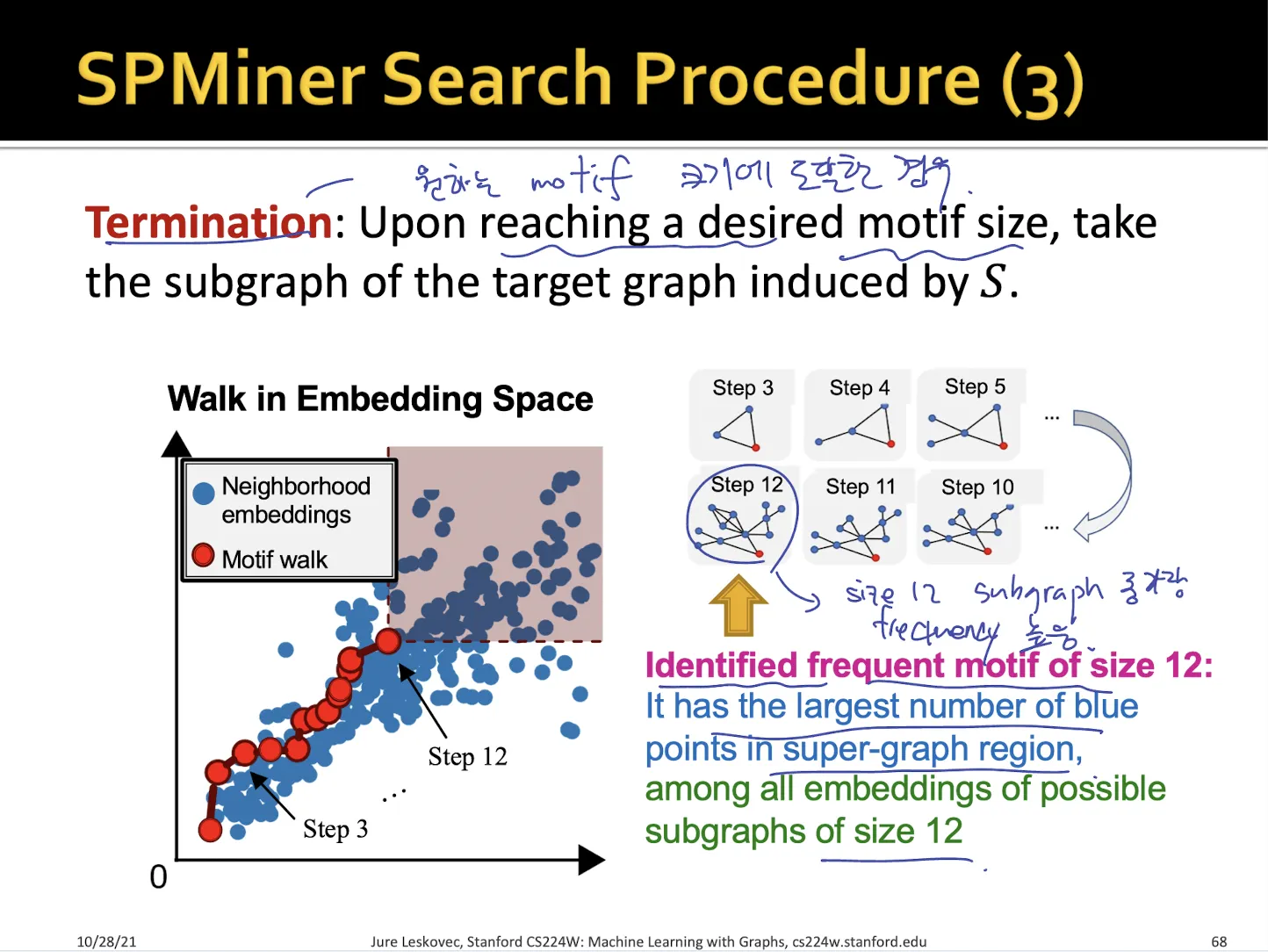
원하는 size에 도달하면 끝낸다.
•
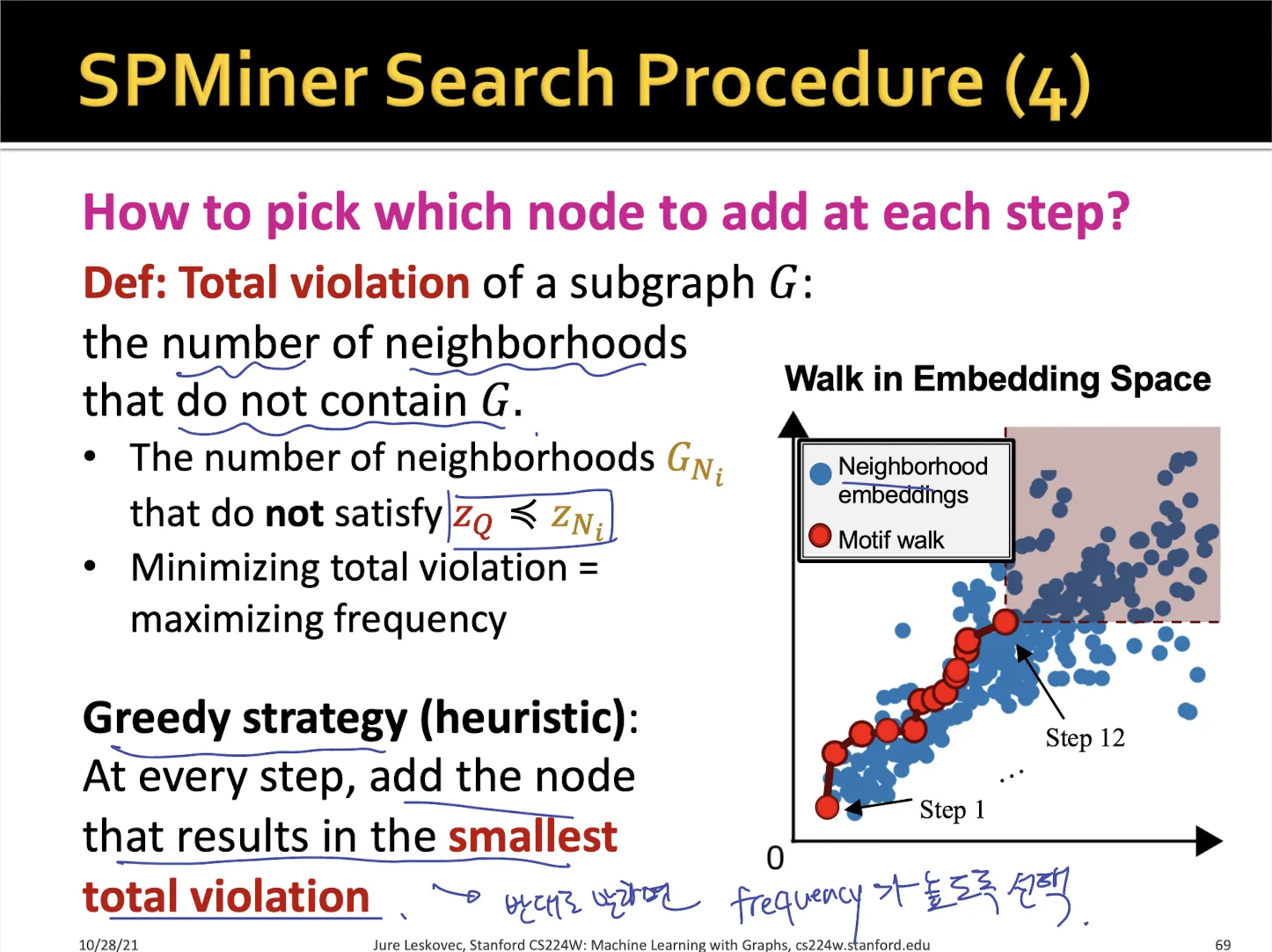
size가 커지는 매 step마다 total violation이 가장 작은 node를 추가하여 motif를 찾는다. (greedy algorithm)
•
total violation은 해당 motif가 포함되지 않은 neighborhoods 들이다.
→ total violation이 작을 수록 motif가 neighborhoods들에 많이 포함되어 있는 걸로 생각할 수 있다.
3.4. Result
•
small motif에 대해서
•
size 9 정도 까지는 실제 frequency를 거의 정확하게 예측하고 있다.
•
y축 : 해당 size에서 가장 많이 등장한 motif의 frequency 수
•
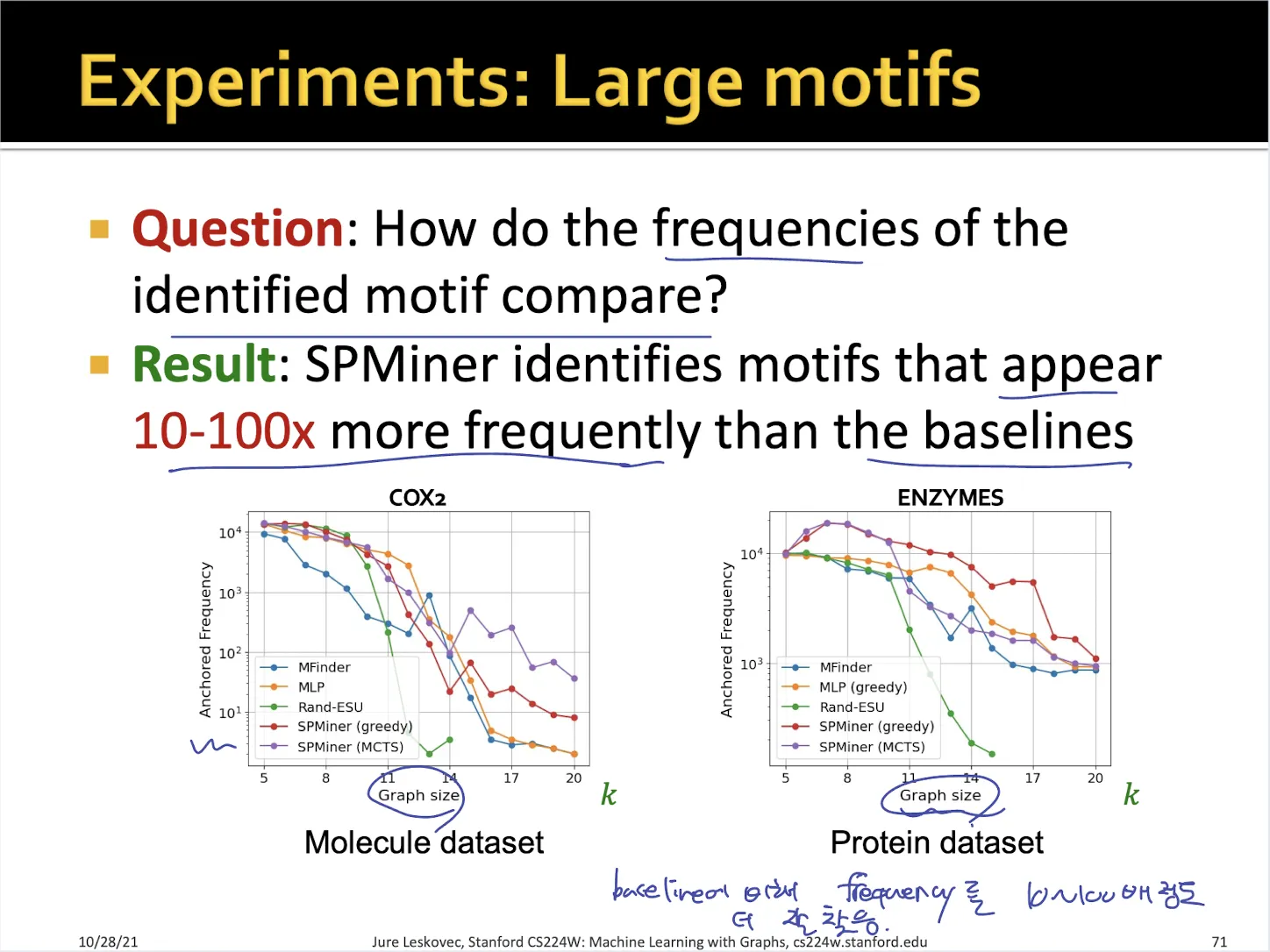
large motif에 대해서
•
large motif의 경우 다른 traditional algorithm에 비해서 더 높은 frequency를 예측함
→ SPMiner를 통해서 frequency가 더 높은 motif를 찾았다고 볼 수 있다.