Search

[CS224W] Lecture 3

Recap

•
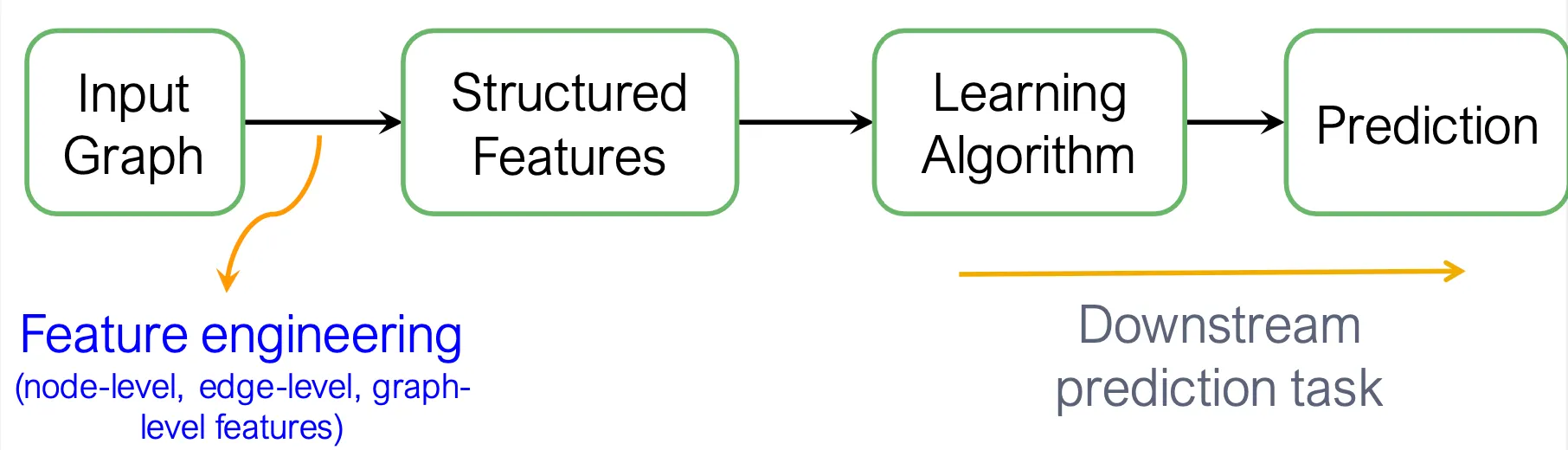
Traditional ML for Graphs
Traditional ML framework은 주어진 input graph에 대해, node-, edge-, graph-level feature를 선택하여 조합하고, SVM, neural network 등의 algorithm을 사용해 최종 prediction을 진행한다.
•
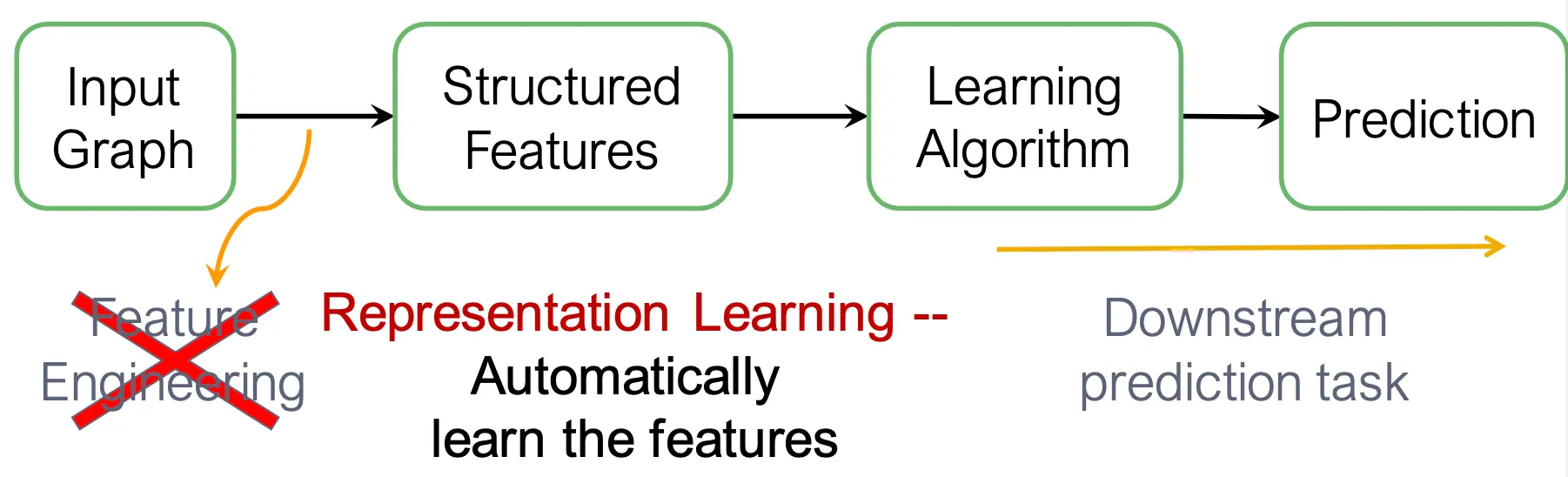
Graph Representation Learning
◦
Representation learning은 manual한 feature engineering 보다는 down stream task에서 필요한 feature를 자동으로 학습한다.
◦
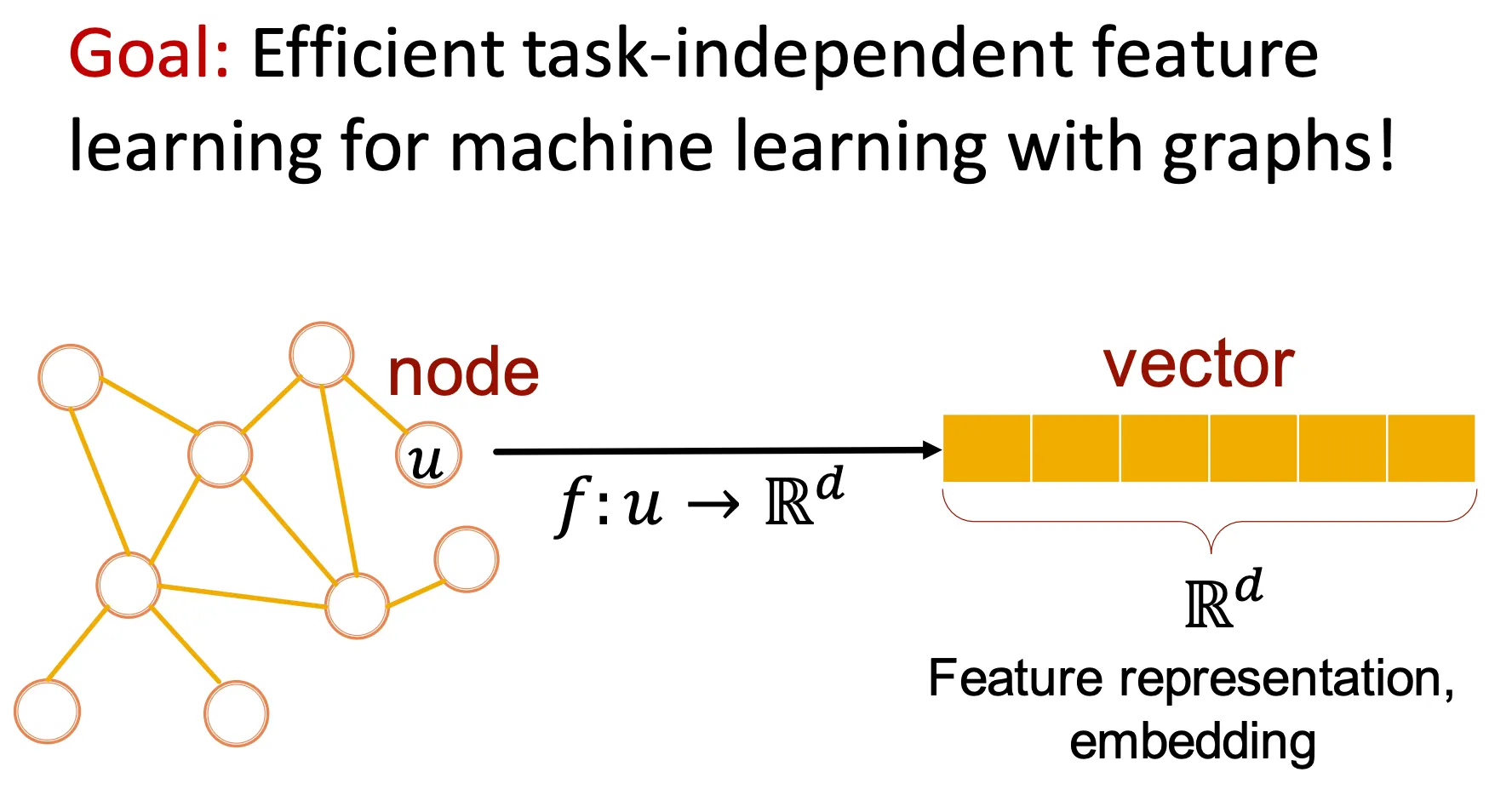
이런 representation learning의 목적은 다양한 task에서 범용적으로 사용할 수 있는 node-, edge-, 또는 graph-level embedding을 얻어내는 것이다.
•
Why Embedding?
◦
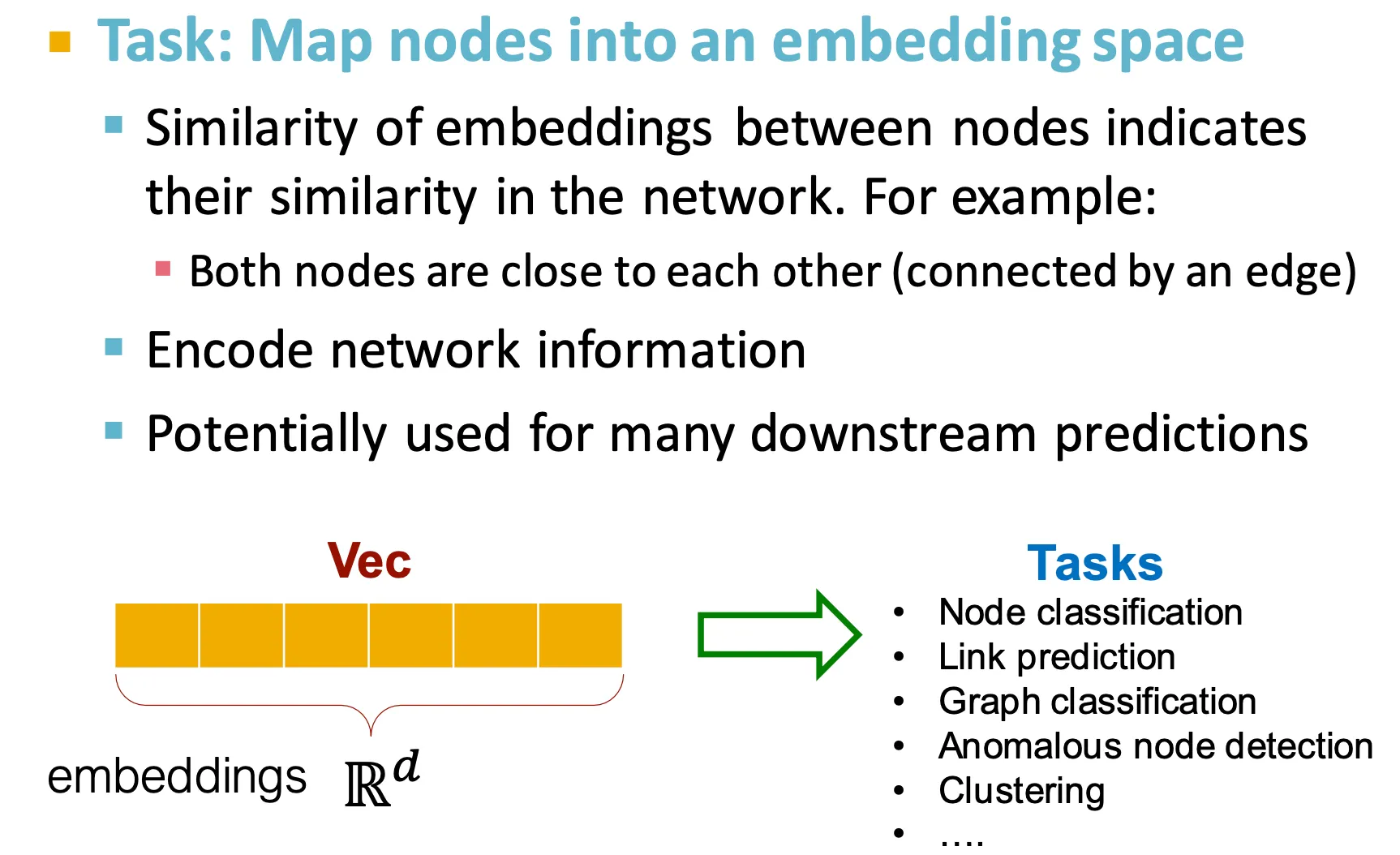
Node를 embedding space로 mapping 하는 task
보통 node들끼리의 embedding의 similarity는 그 node들이 속한 network에서의 similarity를 의미한다.
이런 embedding은 다양한 downstream prediction에 사용될 수 있다.
•
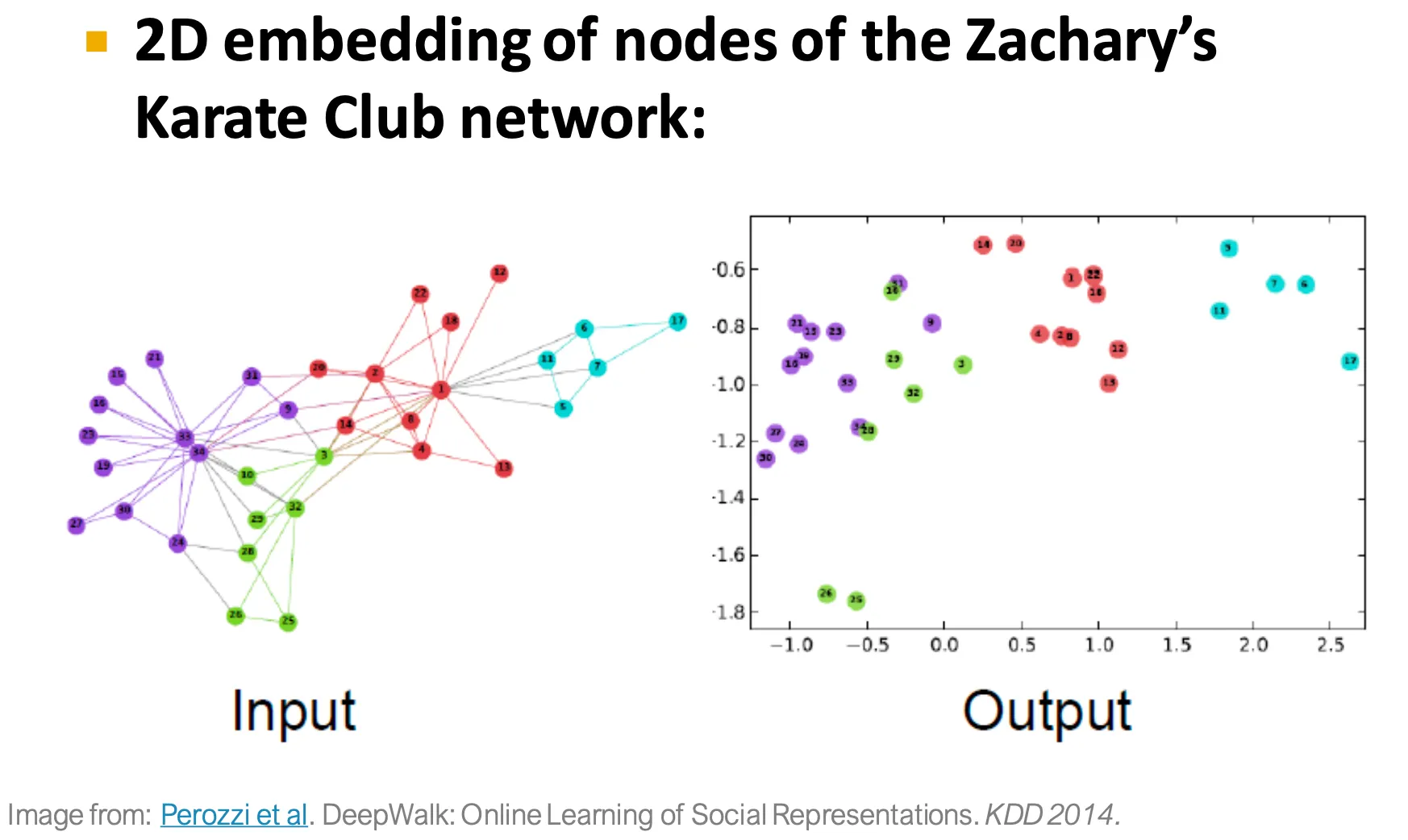
Example node embedding
◦
Input graph를 DeepWalk으로 embedding하여 2D space에 mapping한 결과.

Node Embeddings: Encoder and Decoder

•
Setup
◦
Notation
▪
GG: graph
▪
VV: vertex set
▪
AA: adjacency matrix
여기서는 편의 상 node feature나 다른 추가 정보는 없다고 가정한다.
•
Embedding Nodes
◦
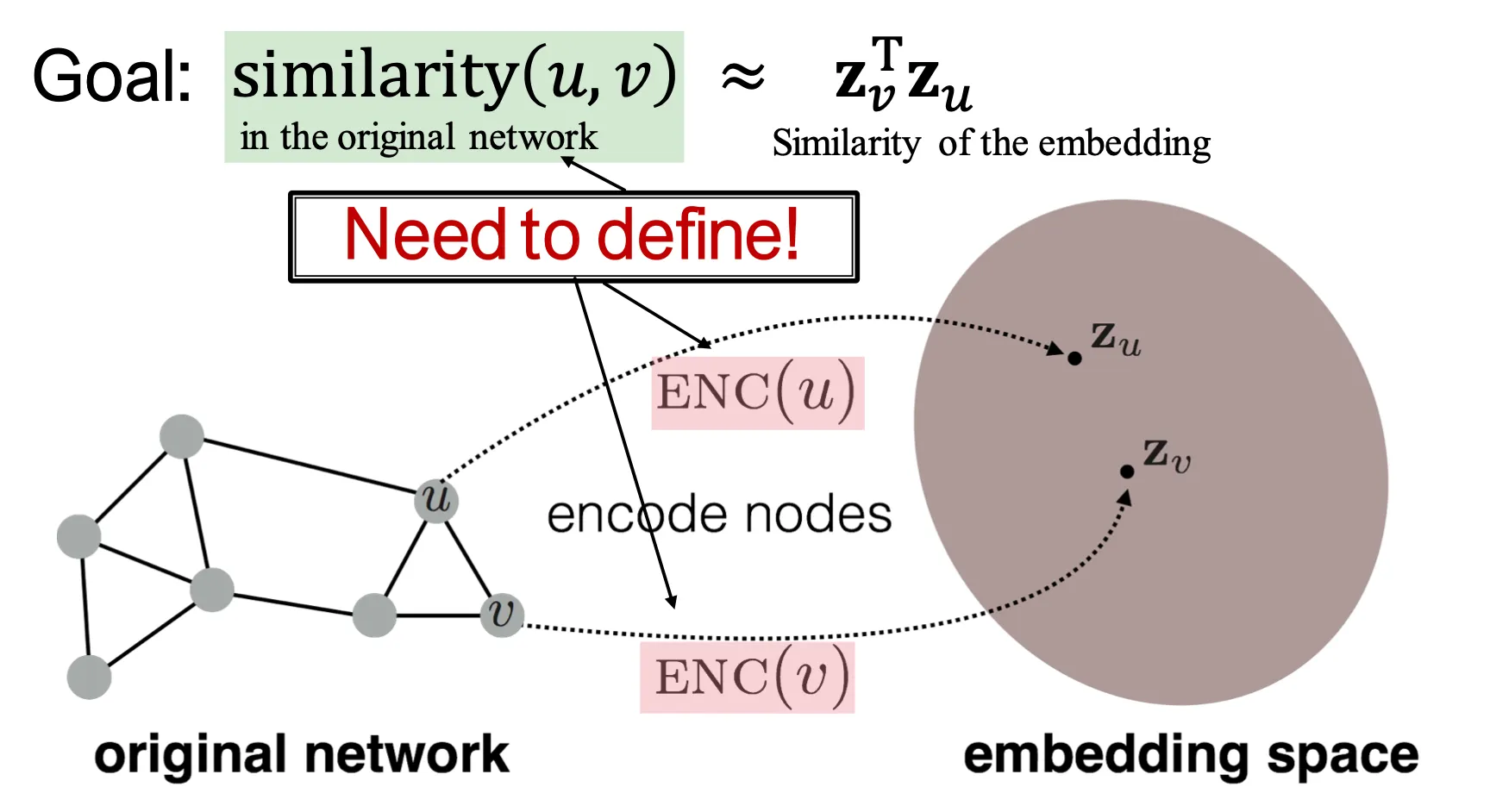
Node embedding의 목적은 embedding space에서의 similarity가 graph에서의 similarity를 반영하도록 하는 것이다.
◦
이를 위해서는 original network에서의 similarity를 먼저 정의해야 한다.
•
Learning node embeddings
◦
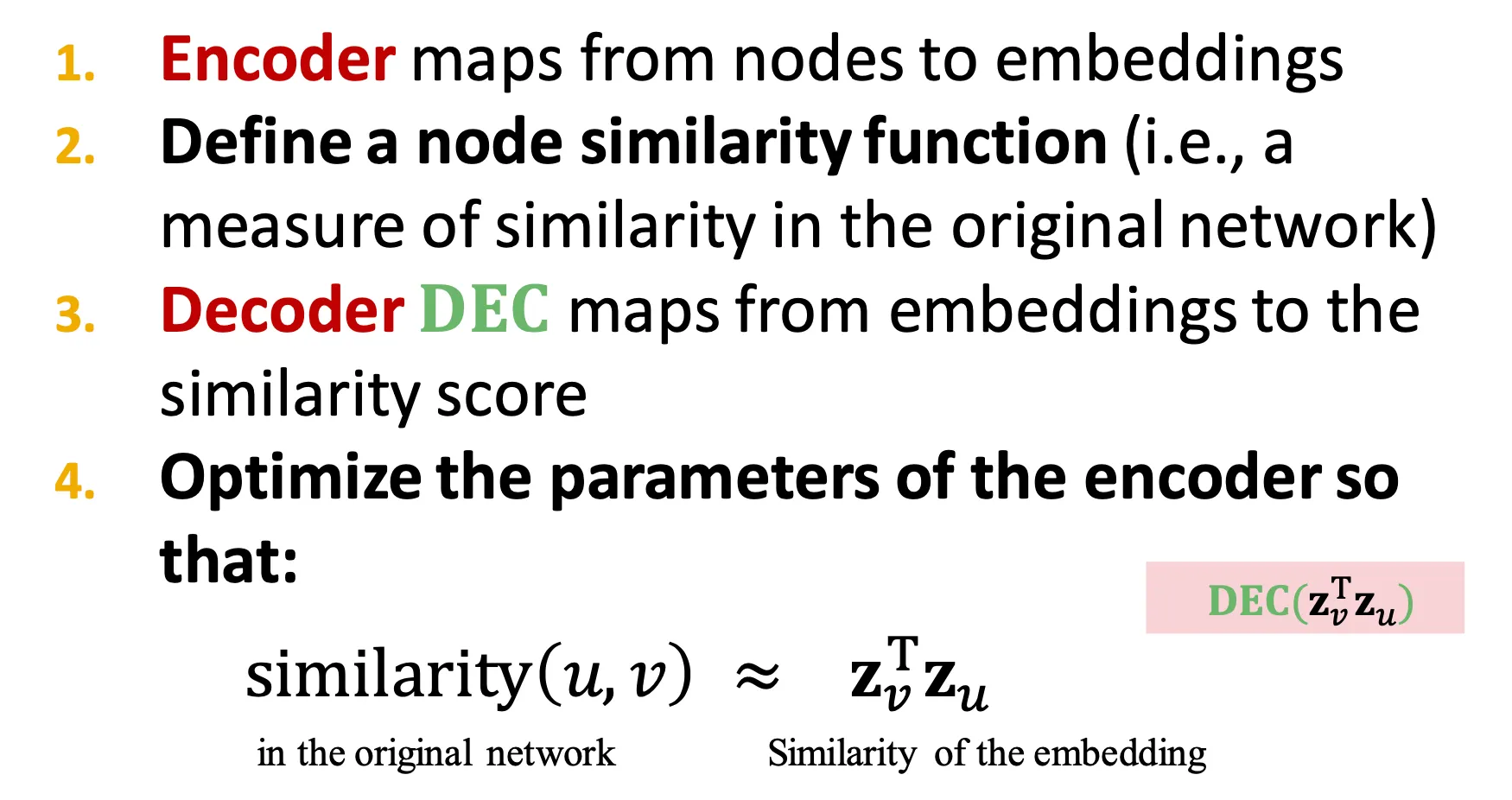
Encoder는 node를 embedding으로 mapping 한다.
◦
Node similarity function을 정의한다.
◦
Decoder는 embedding을 similarity score로 mapping 한다.
◦
Encoder의 parameter를 조정하여 original network에서의 similarity와 embedding vector 간 similarity가 유사하도록 한다.
•
Two key components
◦
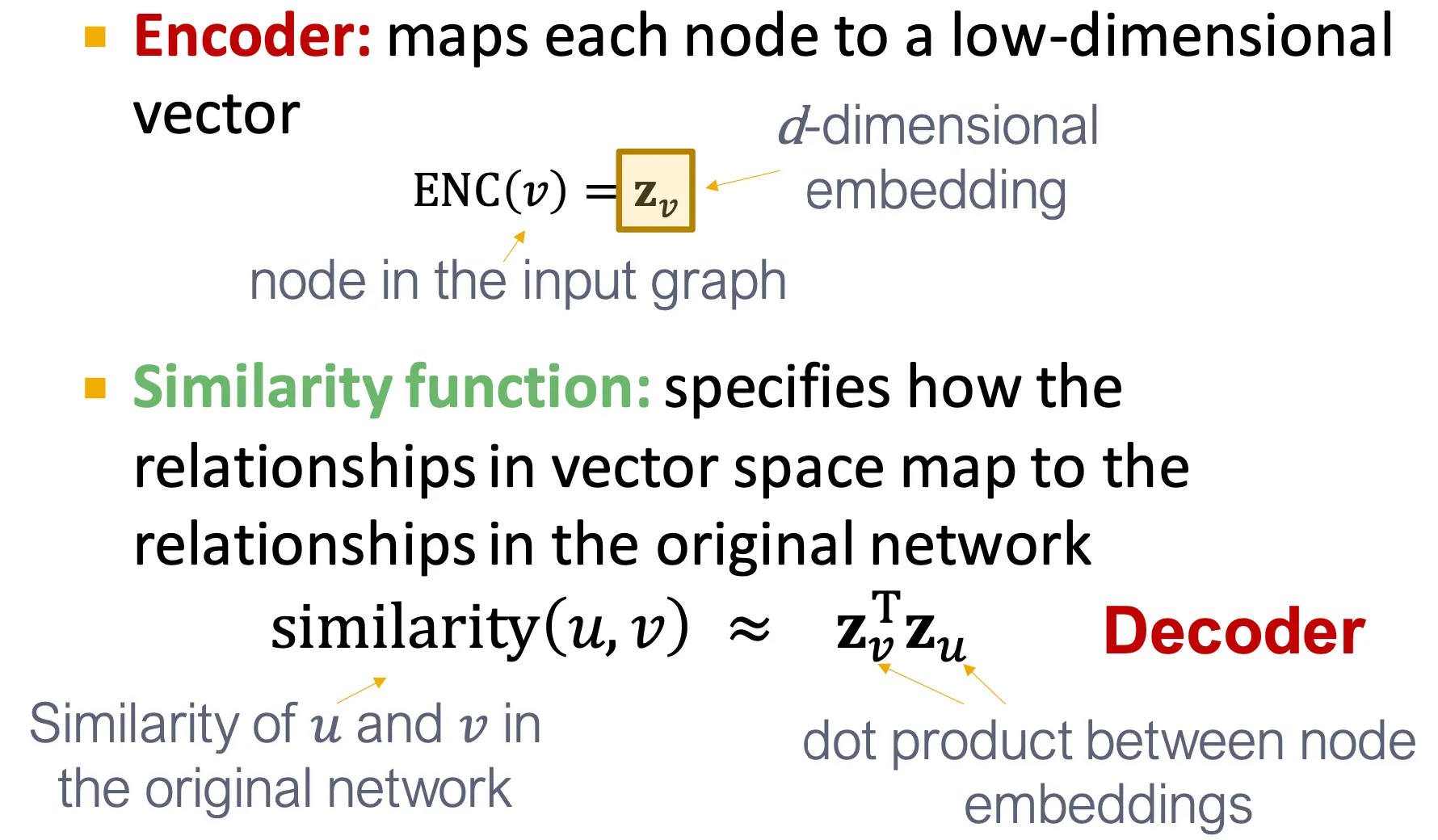
Encoder는 각 node를 low-dimensional vector로 mapping 한다.
◦
Similarity function은 vector space에서의 관계가 original network에서의 관계로 mapping 되는지 정의 한다.
•
Shallow embedding
◦
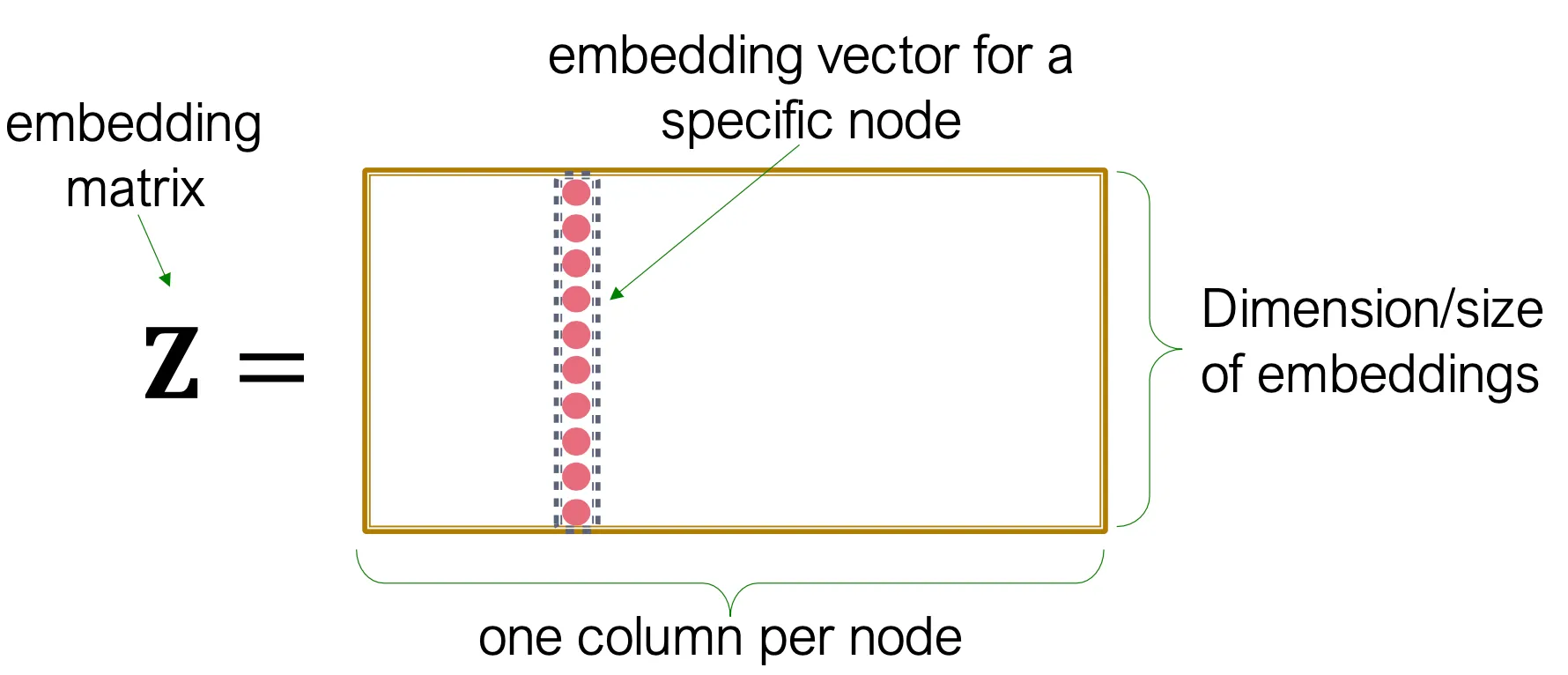
간단하게 생각하면 encoder는 embedding lookup으로 볼 수 있다.
◦
각 column은 그 index에 해당하는 node에 대한 embedding vector를 담고 있다.
◦
각 node는 각 embedding vector로 assign 되고, 직접 이 embedding vector가 optimize 된다.
유명한 방법으로는 DeepWalk, node2vec 등이 있다.
•
Framework summary
•
How to define Node Similarity?
◦
Node similarity를 어떻게 정의하느냐가 매우 중요하다.
ex) 두 node가 연결이 되어 있거나, neighbor를 공유하거나, structural role이 비슷하거나…
◦
앞으로 random walk을 활용한 node similarity definition에 대해 공부할 것이다.
•
Note on Node Embeddings
◦
Random walk을 활용한 node embedding 방법은 unsupervised / self-supervised 방법이다.
▪
Node label이나 feature를 추가적으로 활용하지 않는다.
▪
이 방법의 목적은 network structure를 유지하는 coordinate를 estimation 하는 것이다.
▪
이 embedding들은 task에 의존적이지 않다.

Random Walk Approaches for Node Embeddings

•
Notation
◦
zu\mathbf{z}_u: node uu의 embedding
◦
P(v∣zu)P(v | \mathbf{z}_u): node uu에서 시작하여 node vv를 visit할 확률
•
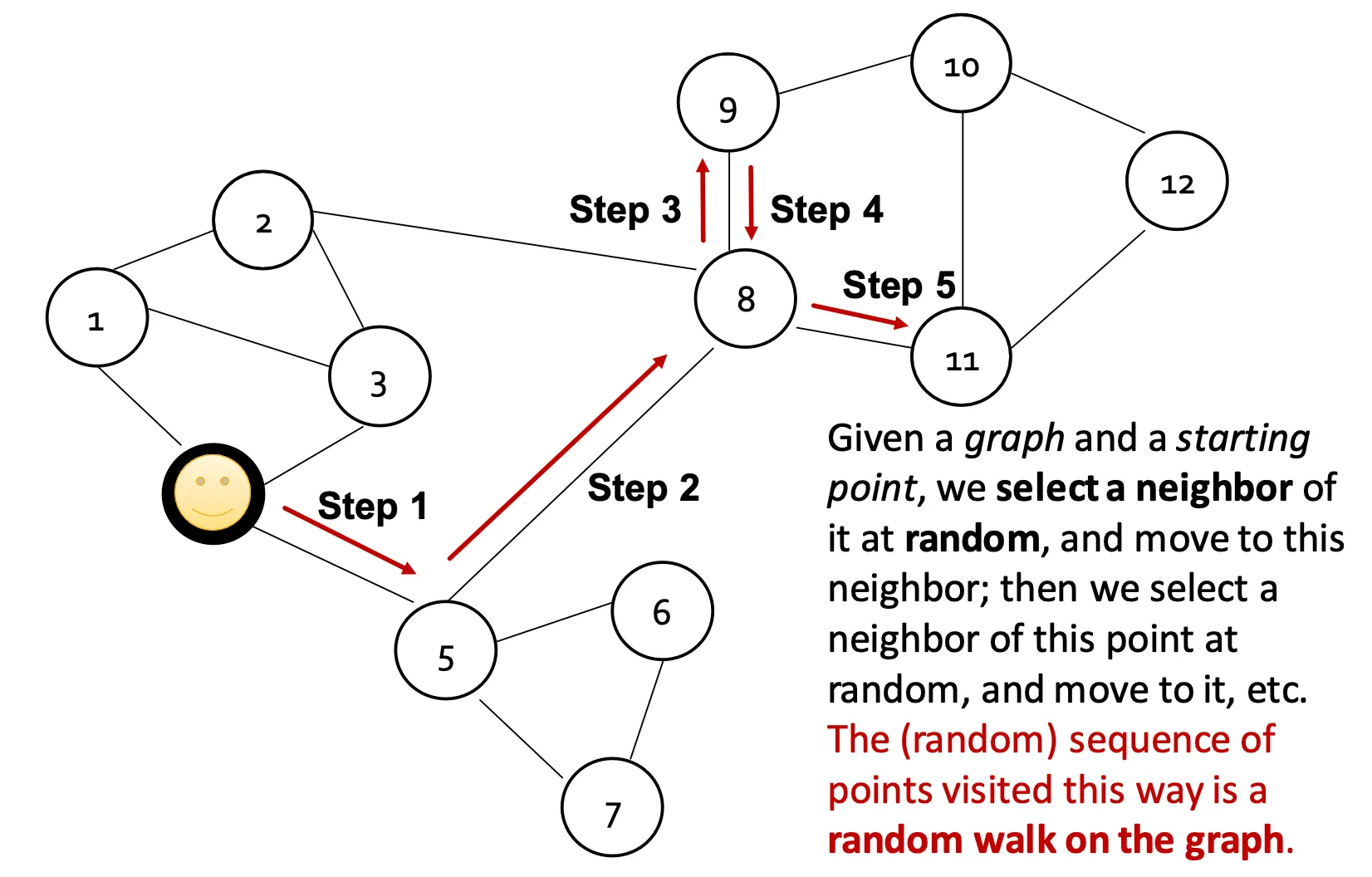
Random Walk
•
Random Walk Embeddings
◦
zu⊤zv\mathbf{z}^\top_u\mathbf{z}_v: random walk해서 node uu와 vv가 같은 walk에 등장할 확률
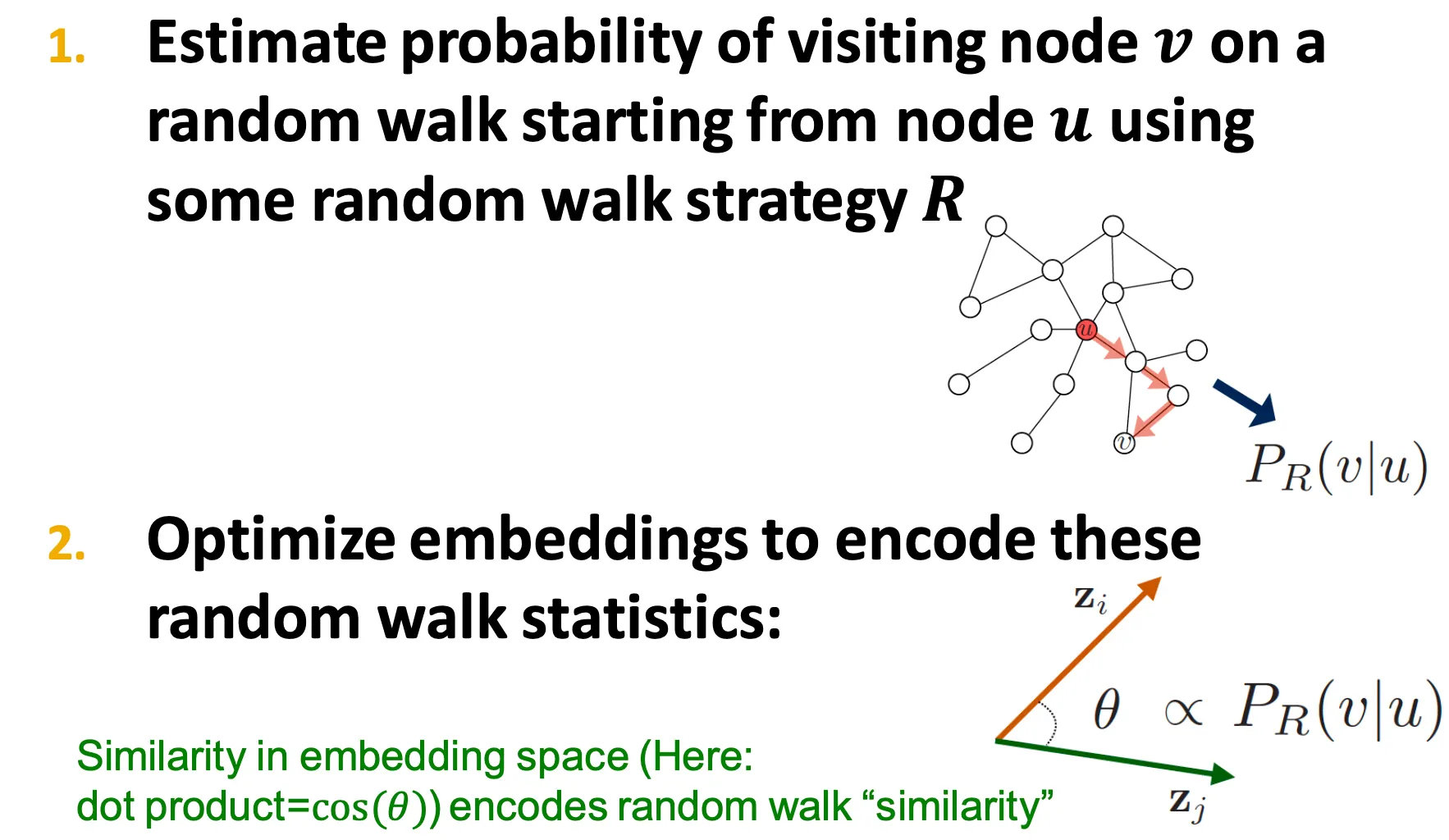
1.
어떤 random walk 방법 RR을 통해 수행하는 random walk에서 node uu 에서 시작해 node vv를 방문할 확률을 estimate 한다.
2.
이 embedding을 원하는 similarity measure에 맞게 optimize 한다.
•
Why Random Walks?
◦
Random walk을 수행하는 이유
1.
Expressivity
Node similarity를 정의하는데에 있어 local과 higher-order neighborhood 정보를 모두 활용할 수 있다.
2.
Efficiency
학습 시에 모든 node pair를 consider 하지 않아도 되고, random walk에 함께 등장하는 node 들끼리의 pair만 고려해도 된다.
Random walk이 많아지면 모든 node pair가 더 efficient 하지 않나..?
•
Unsupervised Feature Learning
◦
이런 random walk 방법은 unsupervised feature learning에 해당하고, 네트워크에서 가까운 node 들을 가깝게 embedding 하는데 목적이 있다.
◦
‘가까운’ node 라고 함은 어떤 random walk 전략 RR 상에서 함께 등장하는 node 들이라고 할 수 있다.
•
Feature Learning as Optimization
◦
수식적으로 optimization problem으로 formulation 해보면,
max⁡f∑u∈Vlog⁡P(NR(u)∣z)\max_f \sum_{u \in V} \log P(N_R(u) | \mathbf{z}) 이다.
즉, 이 log probability를 maximize 하는 node embedding을 찾는 문제이다.
•
Random Walk Optimization
◦
Random walk 수행 순서
1.
어떤 고정된 길이 만큼의 random walk을 수행한다.
2.
각 node에서 시작한 random walk에서 함께 방문된 node 들을 multiset 안에 기록해둔다.
3.
Node uu에서 시작하여 neighbor들 NR(u)N_R(u)을 예측할 수 있도록 embedding을 optimize 한다.
◦
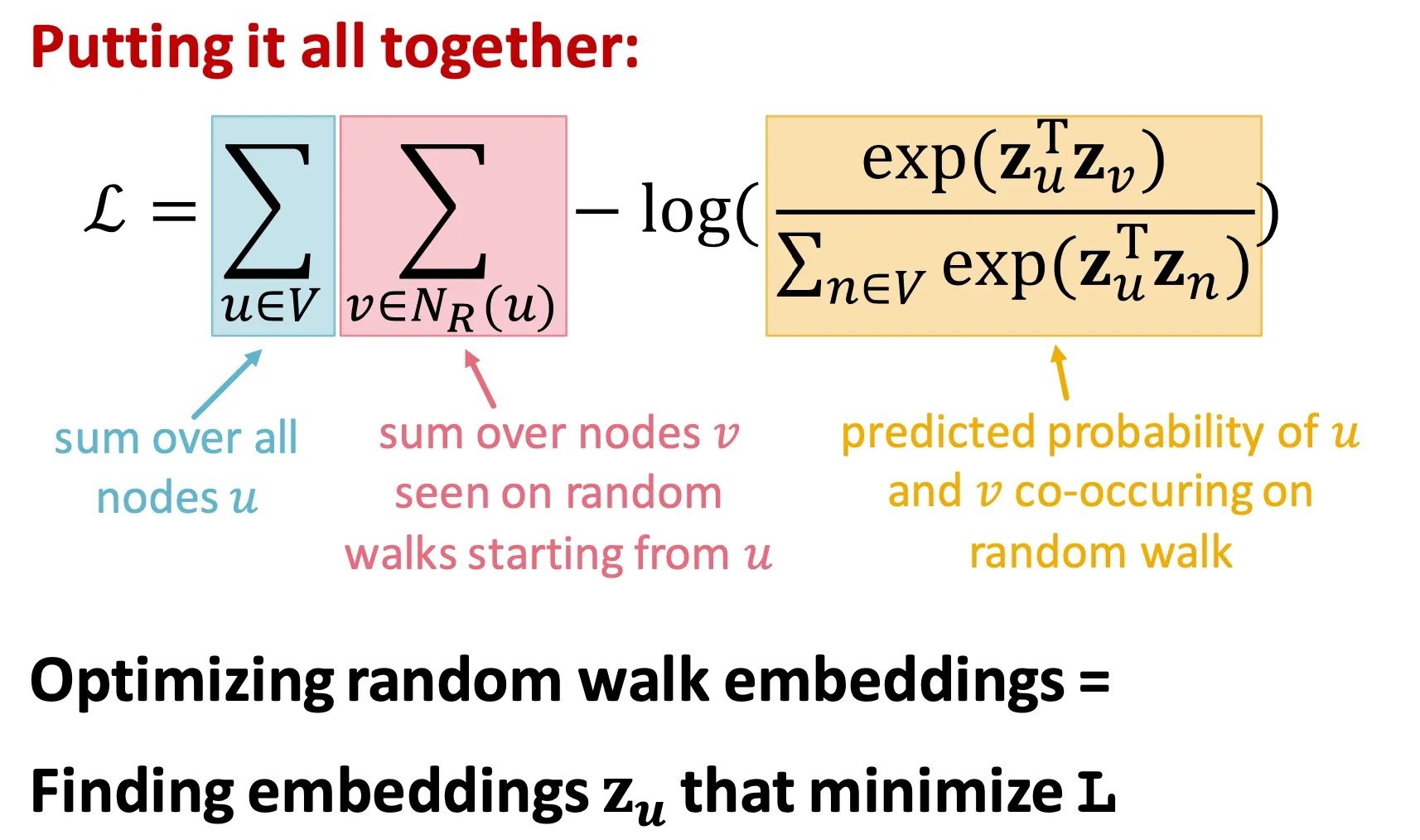
Loss (minimization) 형태로 표현하면 L=∑u∈V∑v∈NR(u)−log⁡(P(v∣zu))\mathcal{L} = \sum_{u \in V} \sum_{v \in N_R(u)} - \log (P(v|\mathbf{z}_u)).
◦
이 때 P(v∣zu)P(v|\mathbf{z}_u)는 softmax를 활용해 exp⁡(zu⊤zv)∑n∈Vexp⁡(zu⊤zn)\frac{\exp(\mathbf{z}^\top_u \mathbf{z}_v)}{\sum_{n \in V}\exp(\mathbf{z}^\top_u \mathbf{z}_n)} 로 parametrize 할 수 있다.
▪
Softmax를 활용하는 이유는 모든 node들(nn) 대비 같은 random walk에 등장하는 node(vv)가 더 비슷하게 embedding 되게 하기 위해서 이다.
◦
하지만 이를 naïve하게 optimize 하면 굉장히 오래 걸린다.
이는 normalization term (분모)이 모든 node 들에 대해 계산해야 하기 때문이다.
이를 approximation 할 수 없을까?
•
Negative Sampling
◦
한 가지 방법은 negative sampling을 해서 분모 term으로 사용하는 것이다.
◦
kk개의 negative sample을 뽑아서 사용한다고 했을 때,
kk가 높아지면 estimate가 더 robust 해지고, negative event에 더 bias가 실린다.
•
Stochastic Gradient Descent
◦
Optimization은 neural net에서 많이 사용하듯이 SGD를 쓸 수 있다.
•
Random Walks: Summary
•
How should we randomly walk?
◦
DeepWalk, ‘13
▪
가장 간단한 방법으로, 정해진 길이만큼의 unbiased random walk을 모든 node들에 대해서 수행할 수 있다.
•
node2vec: biased walks
◦
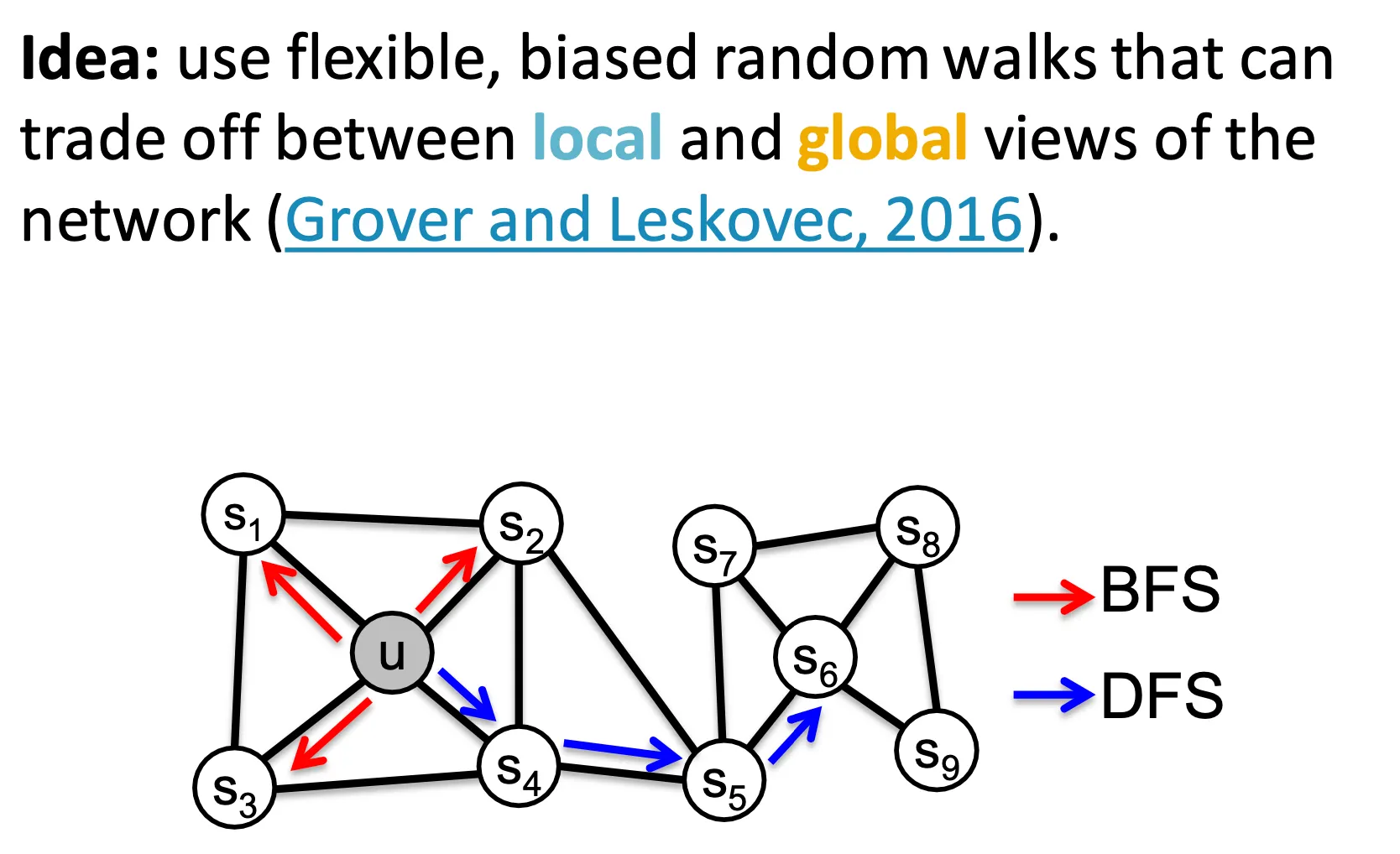
node2vec의 idea는 biased 2nd order random walk을 수행하여 local 및 global view를 담는 것이다.
▪
DeepWalk의 generalization 이라고 할 수 있다.
◦
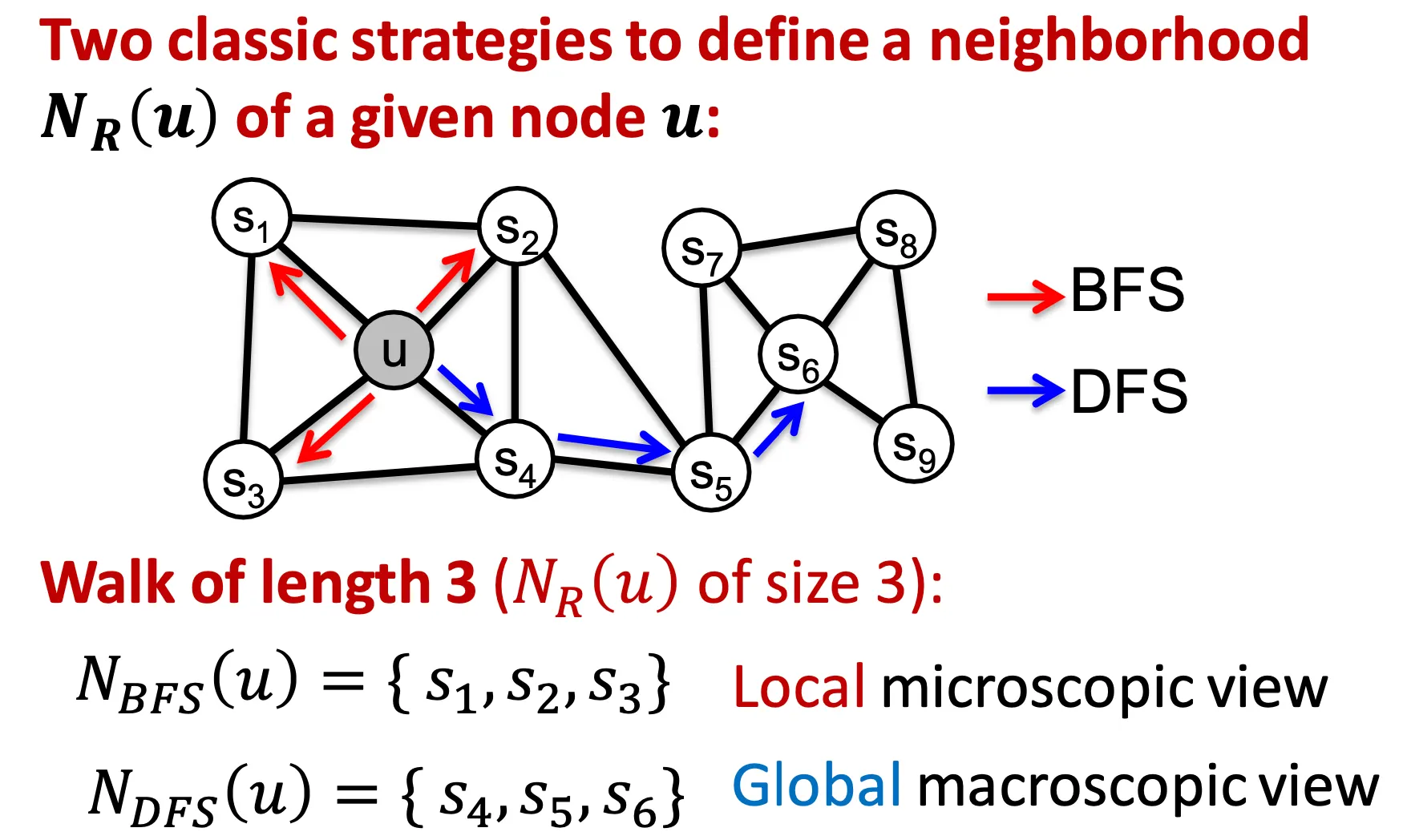
Local view는 BFS, global view는 DFS 스타일로 수행한다.
•
Interpolating BFS and DFS
◦
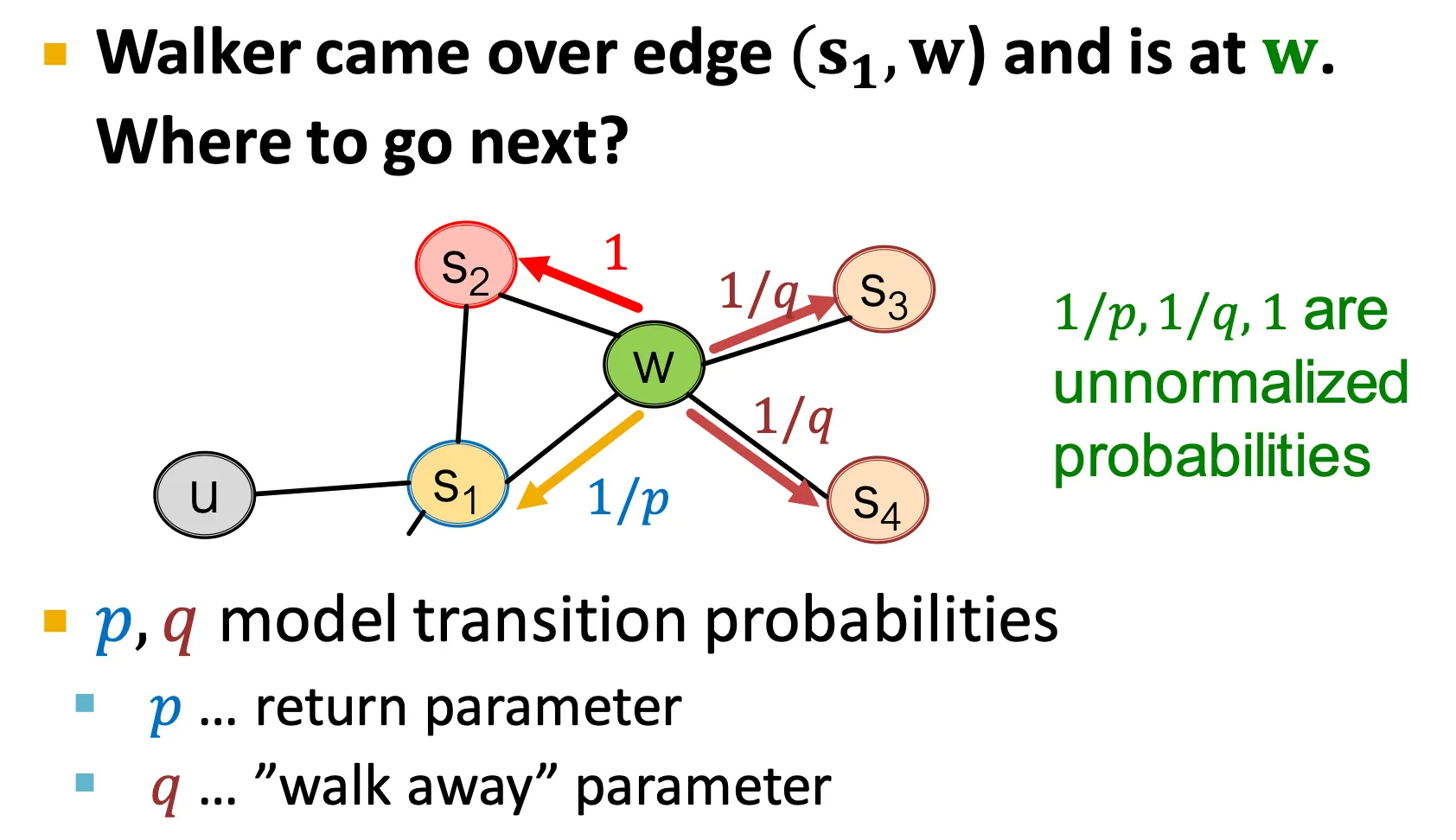
node2vec은 두 가지 parameter 를 사용한다.
▪
pp: return parameter
기존 node로 돌아오는 확률
▪
qq: in-out parameter
BFS, DFS 중 어떤 쪽에 더 가중치를 줄지 정하는 확률
•
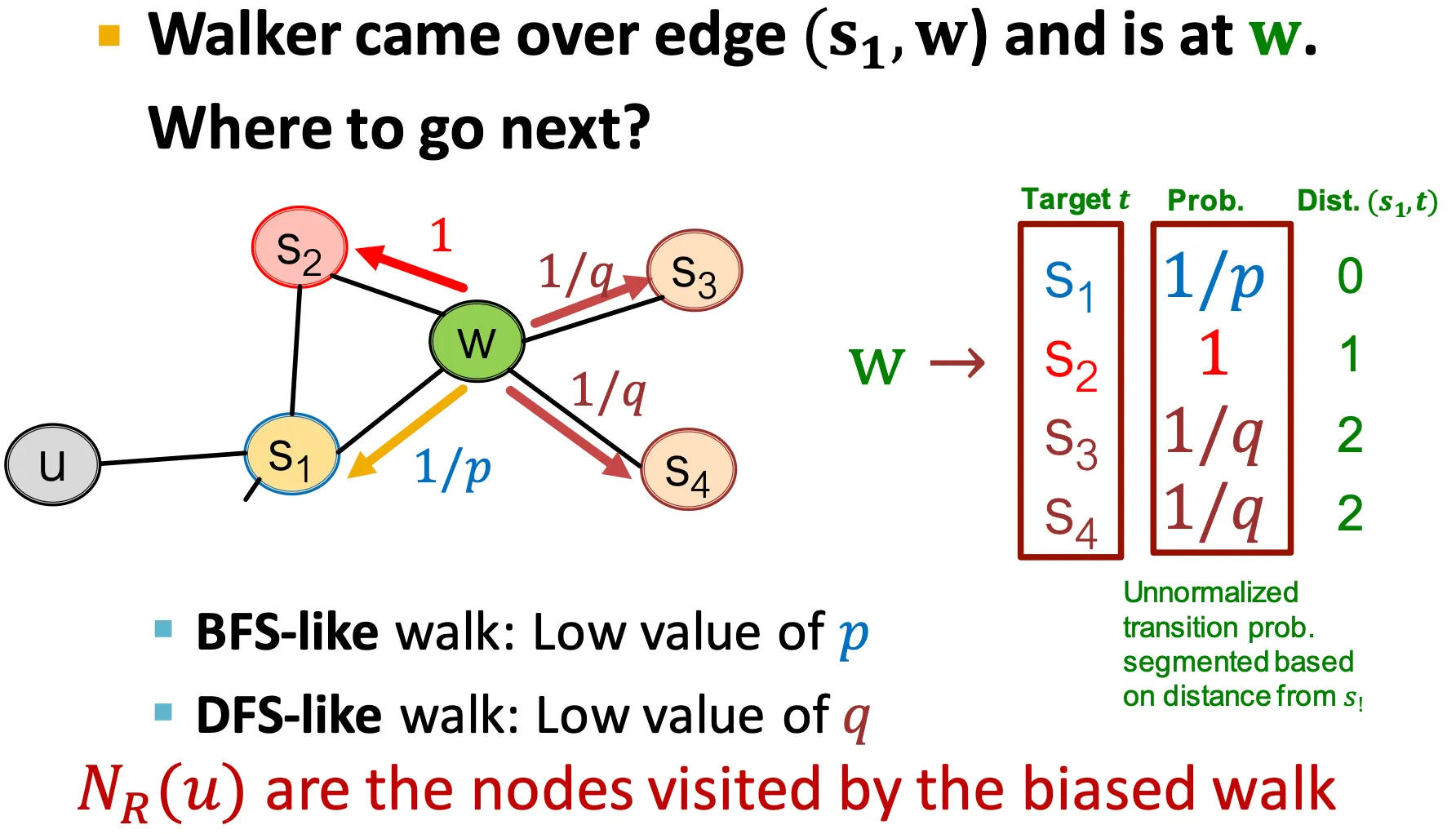
Biased Random Walks
◦
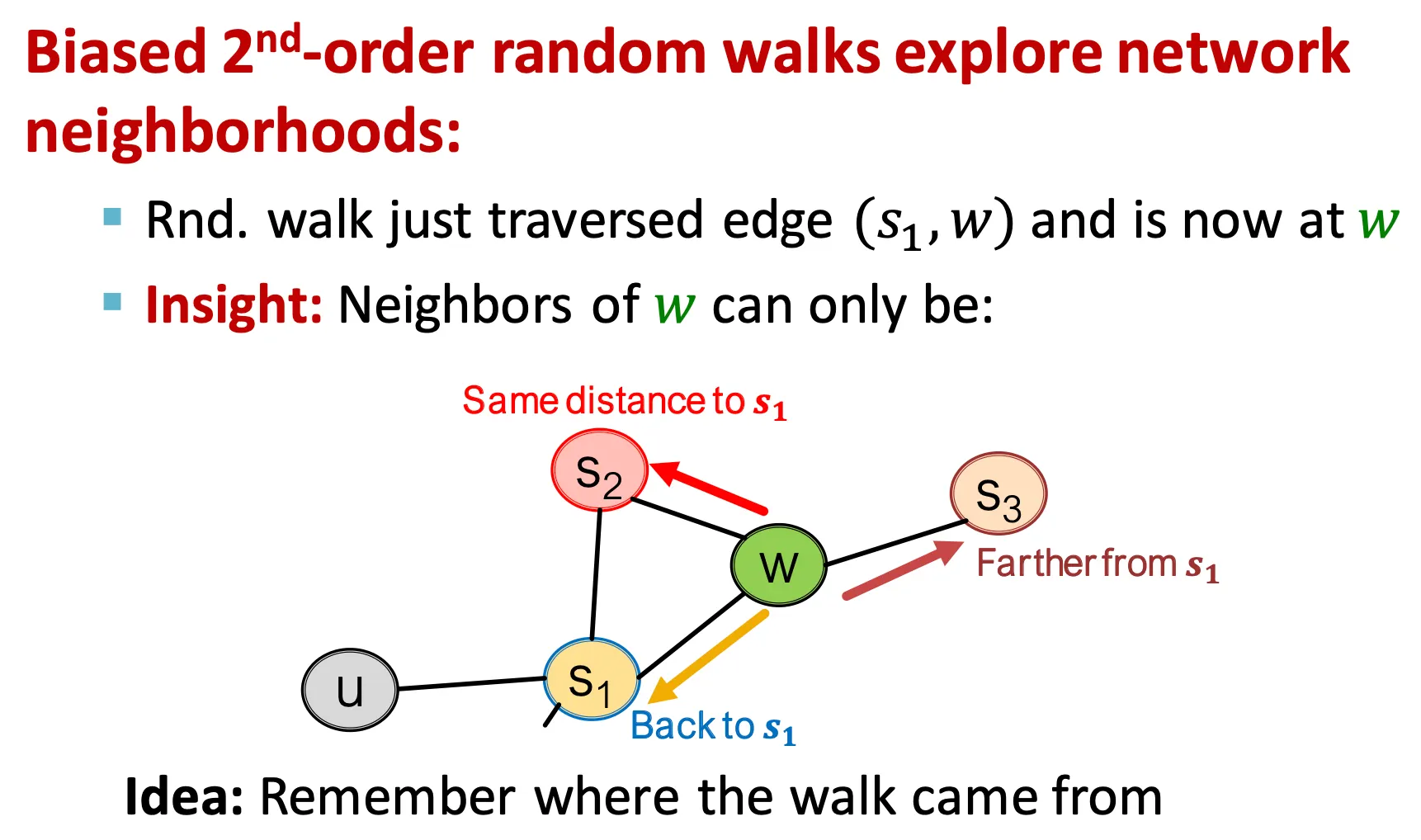
기본으로 이전 node를 기억한다.
▪
이전 node와 다음으로 이동할 node 사이의 거리를 기준으로,
0: 이전 node 다시 방문
1: 이전 node와 현재 node와 모두 연결된 node 방문
2: 이전 node에는 연결되어 있지 않고, 현재 node와만 연결된 node 방문
▪
pp가 낮을수록 BFS 스타일의 random walk 수행
▪
qq가 낮을수록 DFS 스타일의 random walk 수행
•
node2vec algorithm
◦
node2vec은 linear time complexity이며, parallelizable 하다.
•
Other random walk ideas
•
Summary so far
◦
여러 방법이 있지만 모든 경우에 좋은 방법은 없다. 다 해보고 좋은 것 쓰면 된다.

Embedding Entire Graphs

•
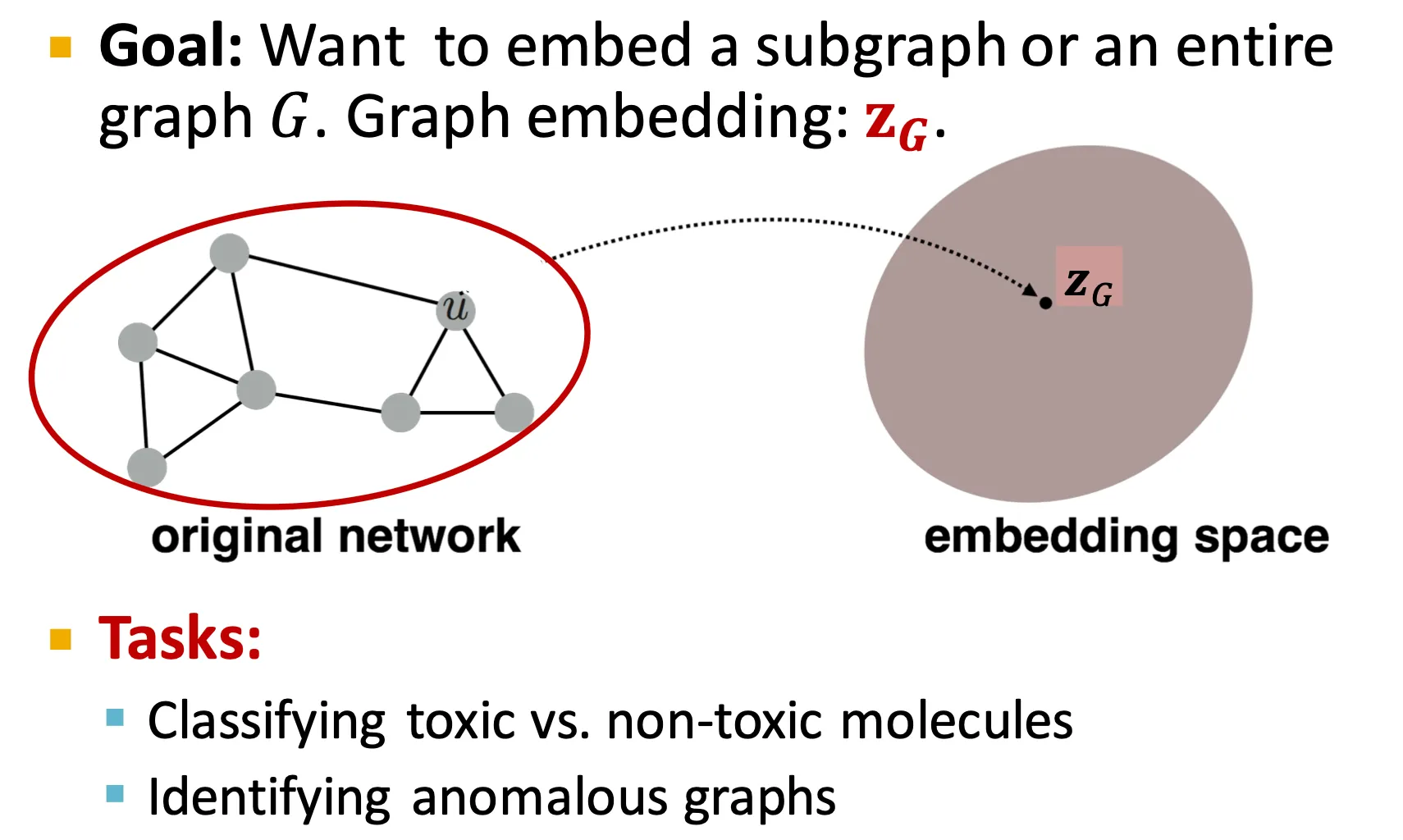
Embedding Entire Graphs
◦
전체 graph를 embedding 해야하는 task들이 있다.
▪
Molecule property prediction
▪
Anomalous graph detection
•
Approach 1
◦
가장 간단한 방법은 node embedding 들을 sum 또는 average 하는 방법이다.
•
Approach 2
◦
두 번째 방법은 특정 (sub)graph의 모든 node들에 연결된 virtual node를 만들고, 그 virtual node의 embedding을 (sub)graph의 embedding으로 사용하는 것이다.
•
Approach 3
◦
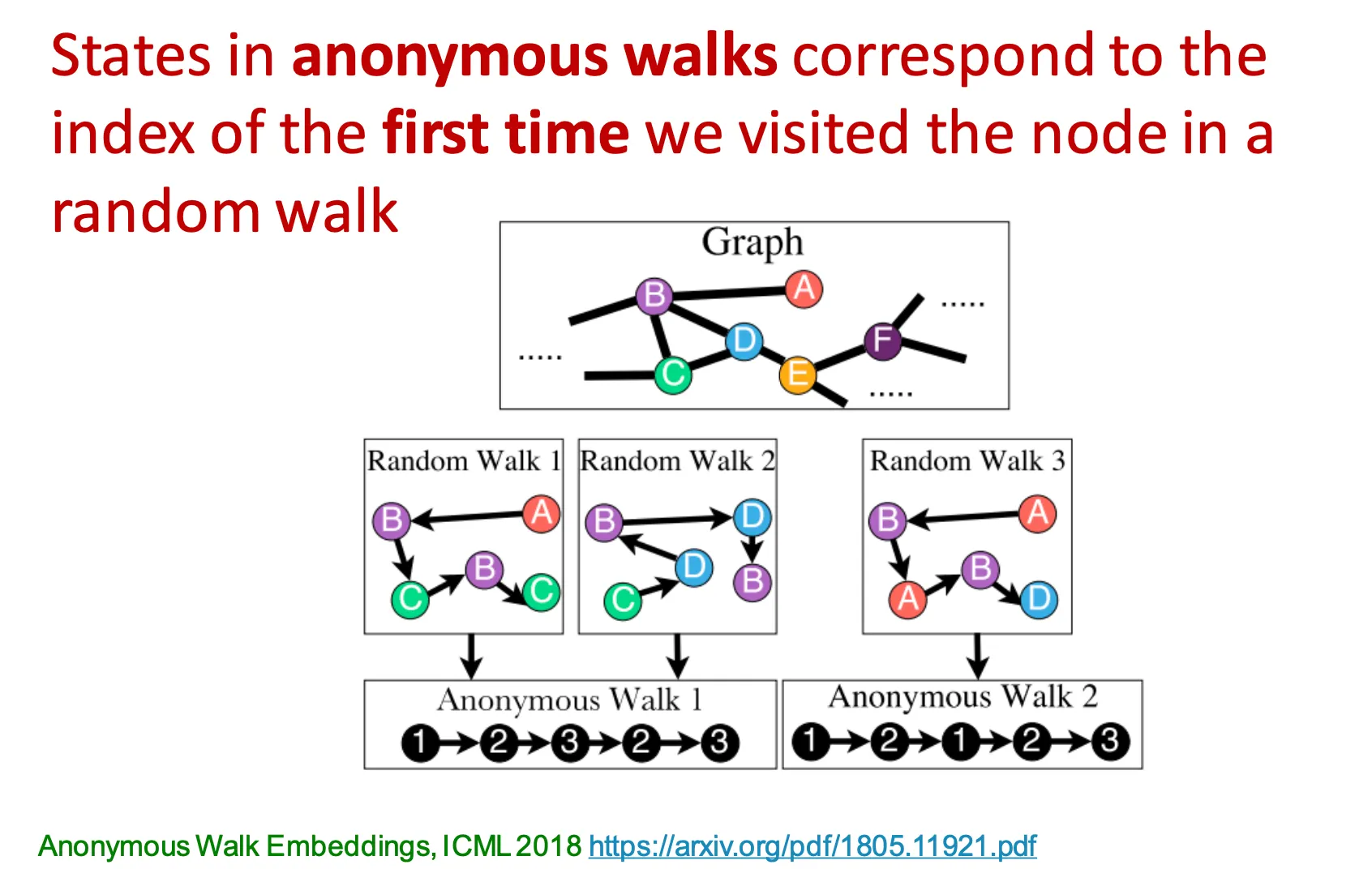
세 번째 방법은 anonymous walk embedding 이라는 방법이다.
Node의 identity와 무관하게 방문했던 node의 ‘순서’를 기억하고 그 walk을 anonymous walk이라고 부른다.
예를 들어, A → B → C → B → C와 C → D → B → D → B 는 동일한 anonymous walk 이다.
•
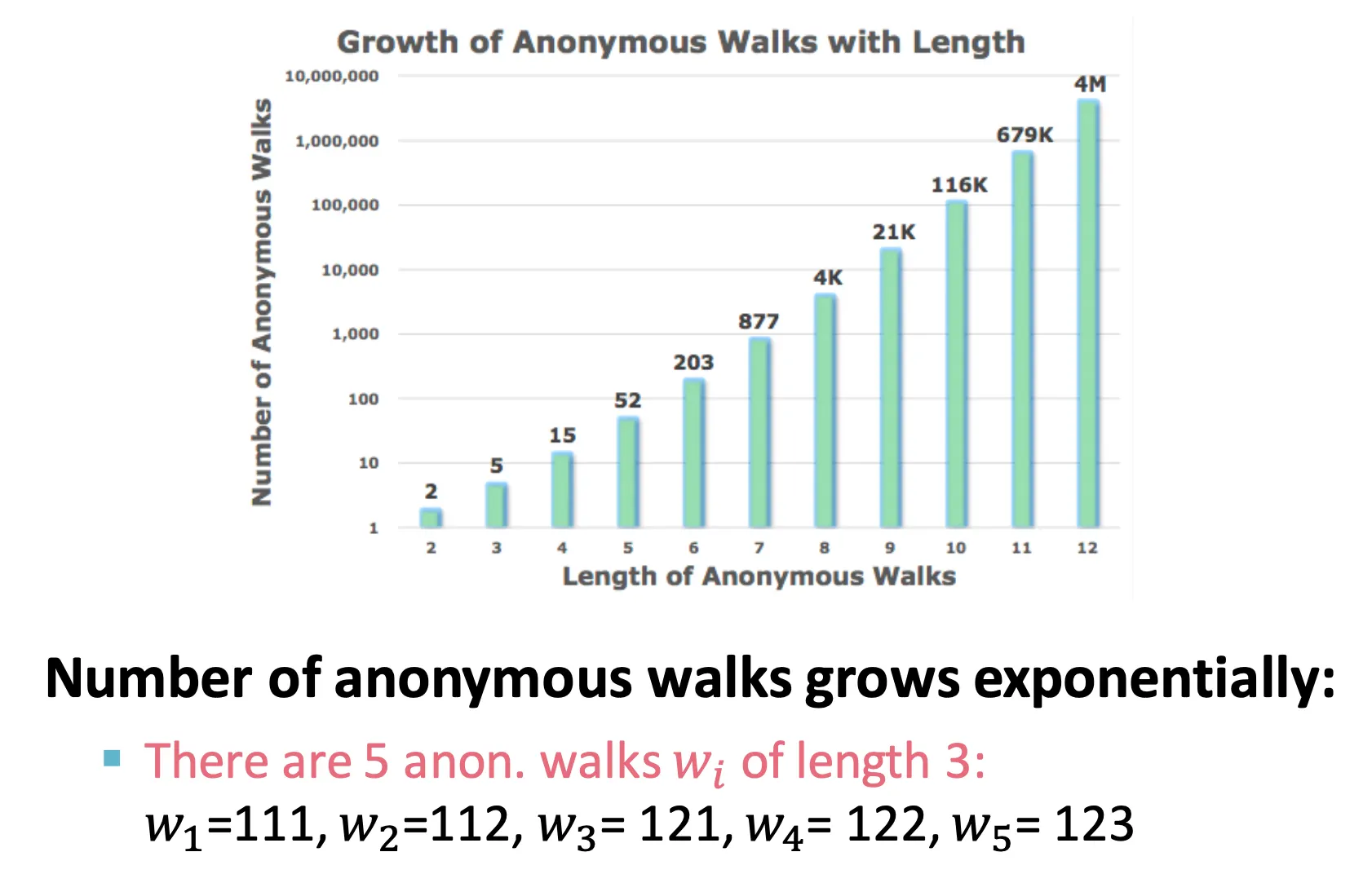
Number of Walks Grows
◦
Walk length에 따라 가능한 anonymous walk의 수는 지수적으로 증가한다.
•
Simple use of anonymous walks
◦
Anonymous walk를 simulation 하고, 그들의 숫자를 센다.
◦
그리고 graph를 이 walk들의 distribution으로 표현한다.
◦
예를 들어, 길이 3짜리 walk은 5 종류가 나올 수 있고, graph를 5-dimensional vector로 표현할 수 있다. Vector의 ii 번째 element는 anonymous walk wiw_i가 등장할 확률이다.
•
Sampling anonymous walks
◦
Anonymous walk을 mm개 sampling 하여 사용하는데, mm을 정하는 방법은 얼마만큼의 error를 어떤 확률로 원하는지에 따라 결정할 수 있다.
•
New idea: Learn walk embeddings
◦
각 walk를 probability (fraction) 으로 표현하지 말고, 각 walk의 embedding을 학습하는 방법도 있다.
◦
모든 anonymous walk에 대해 embedding zi\mathbf{z}_i를 학습한다.
◦
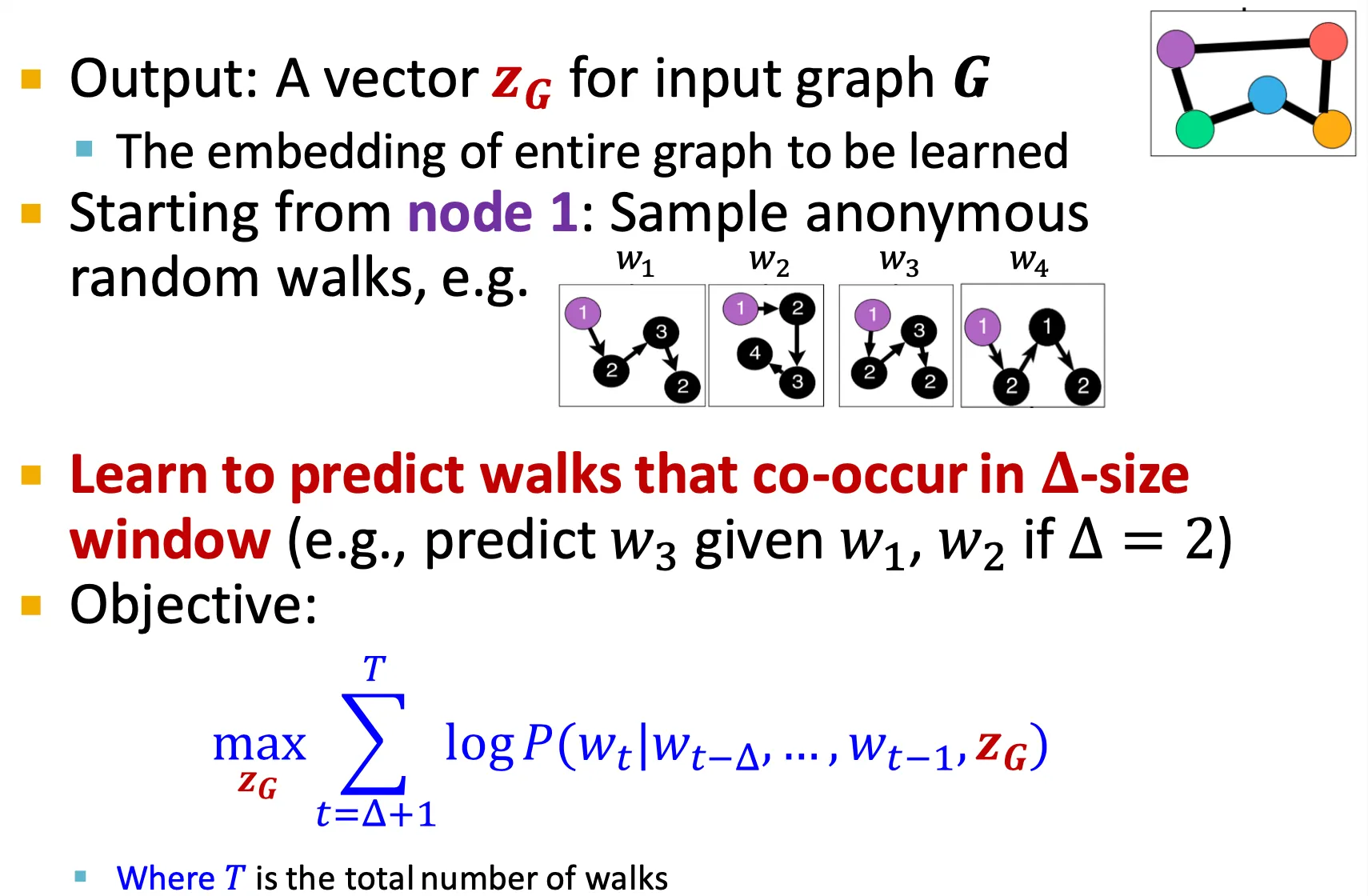
최종 output은 어떤 graph GG에 대한 vector zG\mathbf{z}_G 이다.
◦
Node 1부터 시작하여 어떤 window size 만큼의 walk을 보고 graph의 embedding과 함께 정보로 주고, 그 다음 walk을 예측하도록 할 수 있다.
◦
Node uu에서 길이 ll 만큼의 서로 다른 TT개의 random walk을 수행한다.
◦
이후, 정해진 window size 안에서 동시에 등장하는 walk을 예측하도록 학습한다.
◦
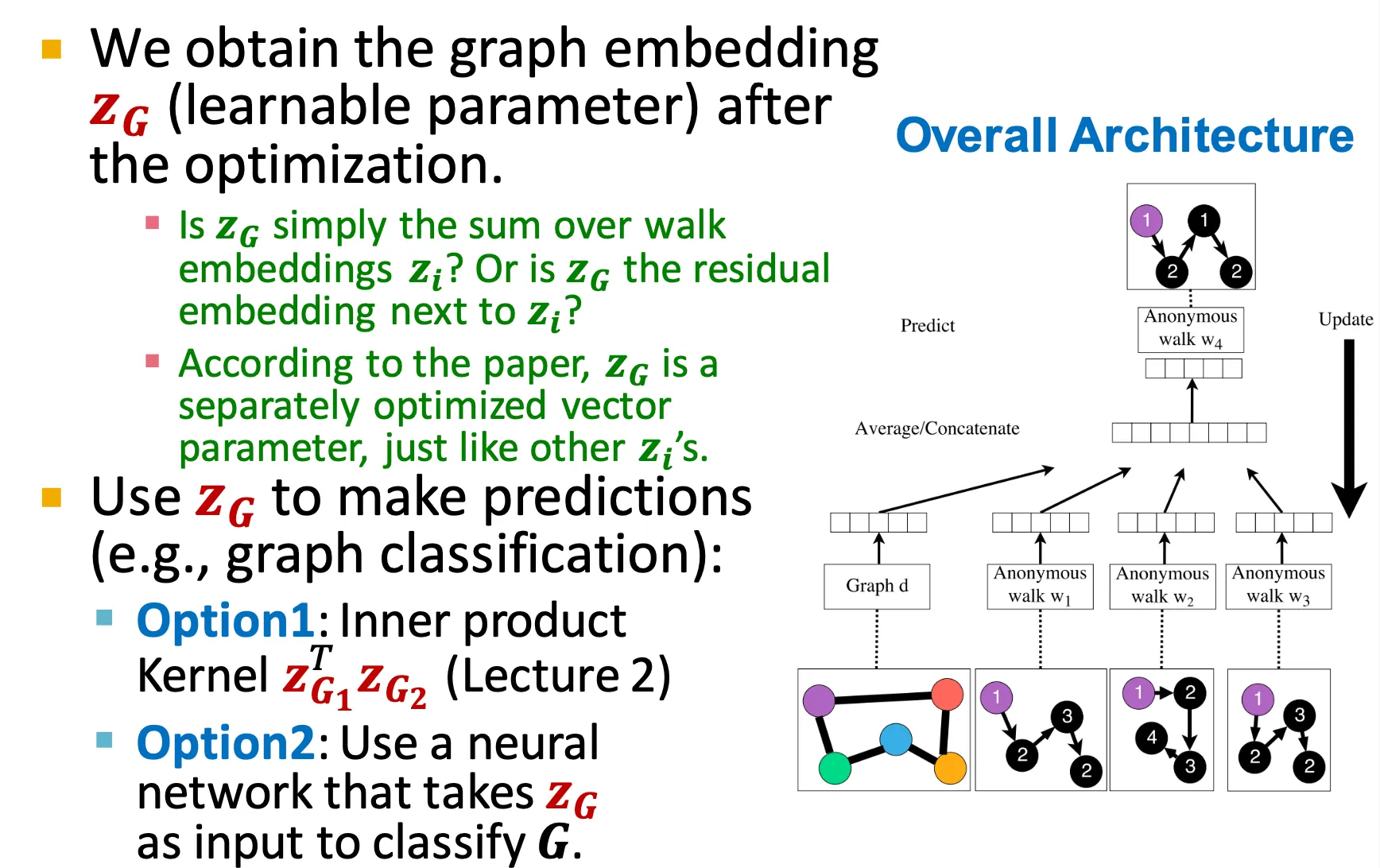
Optimization 시에 graph embedding zG\mathbf{z}_G도 함께 optimize 되며, 이를 downstream task에 사용한다.
•
Summary
•
Preview: Hierarchical Embeddings
◦
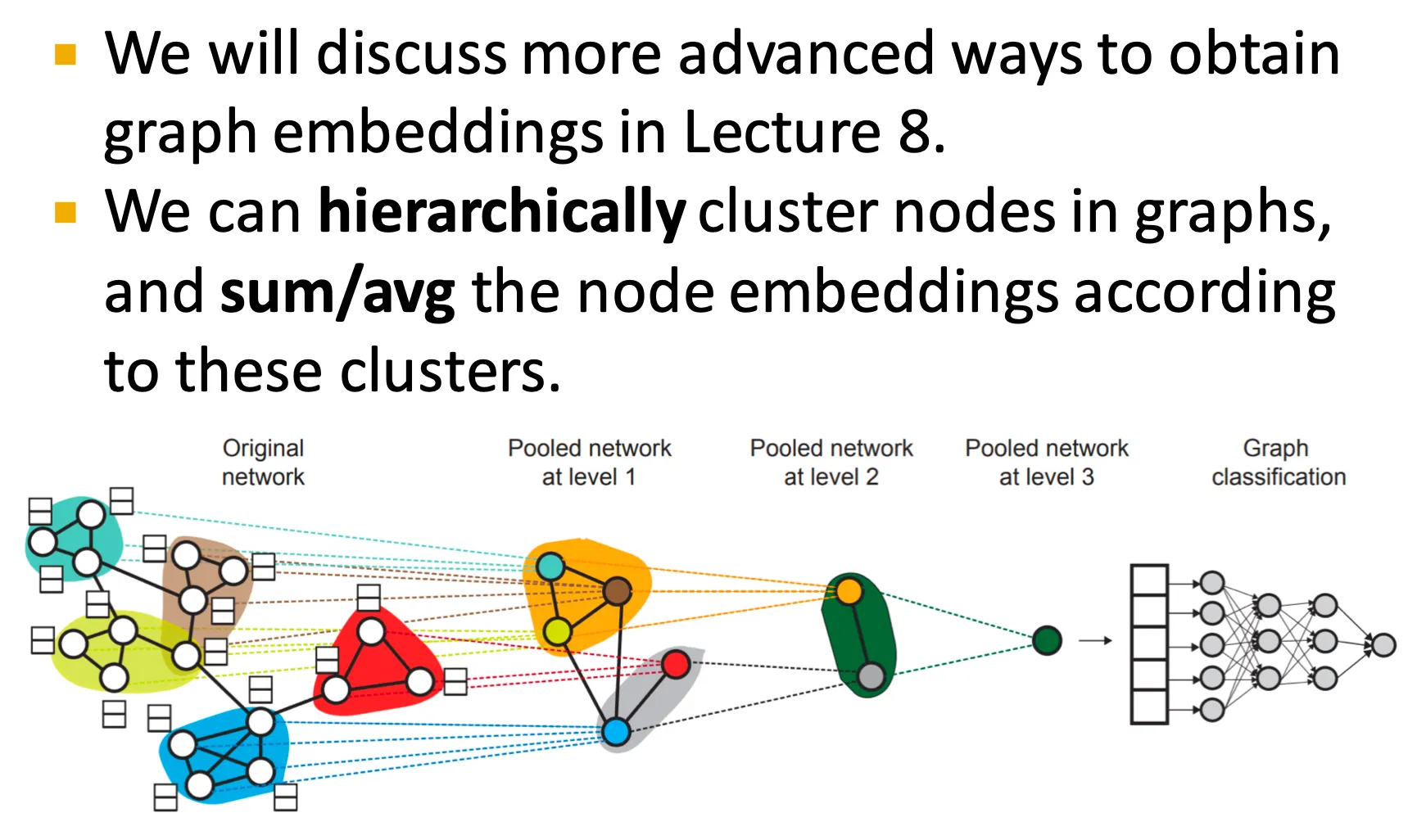
곧 node 들을 작은 group 들로 pooling 하여 사용하는 hierarchical embedding에 대해서도 배운다.
•
How to use embeddings
◦
Node의 embedding은 여러 task에 사용할 수 있다.
▪
Clustering 또는 community detection
▪
Node classification
▪
Link prediction
▪
Graph classification
•
Today’s Summary