Search

Structured Transformer: Generative Models for Graph-Based Protein Design

Generative Models for Graph-baed Protein Design [Paper] [Code]

1. Summary

이 논문의 Contribution은 무엇일까?
•
Protein inverse folding P(sequence|structure)P(\text{sequence|structure)}의 선구자적인 연구이다.
참고: Protein inverse folding은 하나의 구조에 하나의 sequence만 정답이 되는 문제는 아니다.
•
Transformer 기반의 autoregressive & conditional generative model 이다.
•
CATH 라는 단백질 분류 시스템에 따라 구조 기반의 데이터 splitting을 제안하였다.

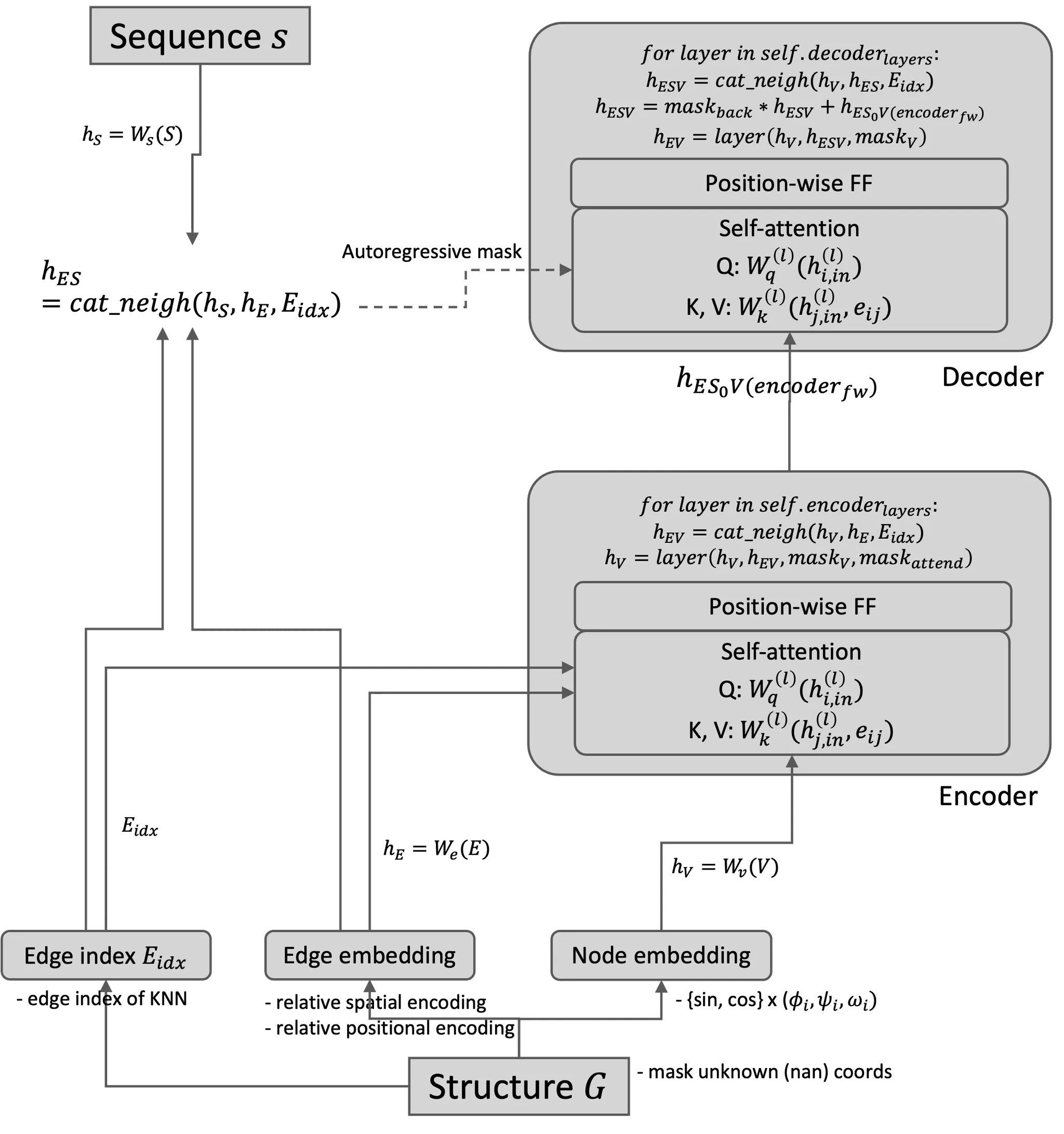
2. Structured Transformer Architecture

A. Input graph에 condition된 language model 형태로 protein design
Encoder, decoder의 input과 output이 각각 뭘까?
Encoder
Decoder
Input
• node embedding • edge embedding (of k-nearest neighbors)
• (refined) node embedding • edge embedding (of k-nearest neighbors) • sequence embedding (teacher forced)
Output
•updated node embedding
predicted next sequence
Encoder는 주변 node의 구조적인 정보만 활용
Decoder는 주변 node의 구조적인 정보 + 이전 timestep 까지의 아미노산 서열 정보도 활용
B. Encoder와 decoder 모두 transformer block 으로 이루어져 있다.
•
Self-attention: neighborhood aggregation
•
Position-wise feedforward: local information

3. Methods

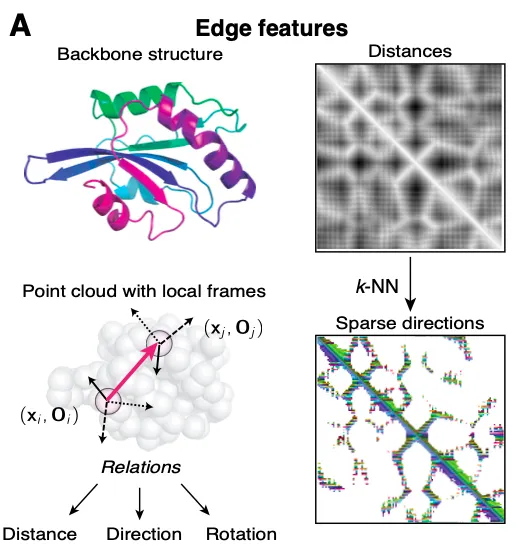
Structure as a graph

단백질 구조를 rigid body라고 생각했을 때, 구조를 잘 나타내기 위해서 만족해야 하는 조건은 무엇일까?
본 논문은 크게 두 가지 조건을 만족해야 한다고 주장한다.
1.
Invariance to rotation & translation
각 feature가 회전과 이동에 대해 invariant해야 한다.
2.
Locally informative
Node viv_i의 이웃들의 정보를 ‘충분히’ 담을 수 있는 feature를 사용해야 모든 이웃 노드들을 reconstruct 할 수 있다.
예를 들어, 노드 간의 ‘거리(distance)’ 만으로는 local coordinate를 유일하게 정의하기 어려운 경우들이 생기므로, 중심축, 방향 등의 정보가 필요할 수 있다.

Features

Node features
각 아미노산 잔기별 node viv_i를 어떻게 표현할 수 있을까?
본 논문은 node feature로 protein backbone의 3가지 dihedral angle (참고: 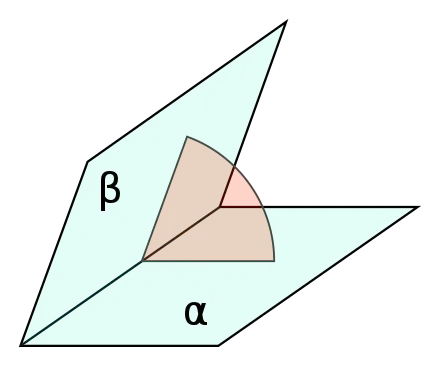Dihedral angle (이면각) 계산하기 - Python ) (ϕ,ψ,ω)(\phi, \psi, \omega)를 계산하고 각각 sin⁡,cos⁡\sin, \cos 값을 node embedding으로 사용한다.
vi=[cos⁡(ϕi),cos⁡(ψi),cos⁡(ωi),sin⁡(ϕi),sin⁡(ψi),sin⁡(ωi)]v_i = [\cos(\phi_i), \cos(\psi_i), \cos(\omega_i), \sin(\phi_i), \sin(\psi_i), \sin(\omega_i)]
Edge features: spatial encodings e(s)e^{(s)} & positional encodings e(p)e^{(p)}
각 아미노산 사이의 관계를 어떻게 표현할 수 있을까?
•
Relative spatial encodings e(s)e^{(s)}
각 아미노산의 CαC\alpha 끼리의 orientation과 rotation을 encoding 하여 eij(s)e^{(s)}_{ij}를 얻는다.
1.
각 point xix_i마다, ‘Orientation’ Oi\mathbf{O}_i를 다음과 같이 정의한다.
Oi=[bi,ni,bi×ni]\mathbf{O}_i = [\mathbf{b}_i, \mathbf{n}_i, \mathbf{b}_i \times \mathbf{n}_i ]
Notation 참고
2.
Final spatial edge feature를 아래와 같이 정의한다.
eij(s)=[r(∥xj−xi∥),OiTxj−xi∥xj−xi∥,q(OiTOj)]e^{(s)}_{ij} = \Big[ r(\|\mathbf{x}_j - \mathbf{x}_i\|), \mathbf{O}^{T}_i\frac{\mathbf{x}_j - \mathbf{x}_i}{\| \mathbf{x}_j - \mathbf{x}_i\|}, \mathbf{q}(\mathbf{O}^T_i\mathbf{O}_j) \Big]
각각 distance, direction, orientation을 담당한다.
q(⋅)\mathbf{q}(\cdot)는 quaternion 형태로 rotation matrix를 표현한 것이다.
•
Relative positional encodings (PE) e(p)e^{(p)}
참고) Vanilla Transformer (Attention is All You Need)에서의 PE
아미노산 서열의 위치를 어떻게 표현하는게 좋을까?
◦
절대적인 위치보다는 상대적인 위치가 중요할 것이다.
◦
이때, 단순히 몇 칸 떨어져있는지도 중요하지만, 누가 앞에 있고 뒤에 있느냐도 중요할 것이다.
본 논문에서는 sequence 상에서의 거리 (좌표 상에서가 아닌) i−ji-j를 sinusoidal function으로 encoding 해준다. 특히, 여기서는 i−ji-j을 절대값이 아닌, 부호까지 그대로 유지하여 encoding 한다 (왜? 일반적인 graph 라면 절대값으로 해도 되겠지만 단백질 서열에서는 누가 앞에 오느냐도 중요하기 때문!)
참고) PE를 이렇게 하는게 일반적일까?
이후 ProteinMPNN (2022)에서는 AF2에서 제안되었던 relative PE 방법을 사용한다.
K-nearest neighbors
Transformer는 O(n2)O(n^2)의 memory & computational complexity가 있기 때문에 모든 이웃 node들을 고려하면 시간이 오래 걸린다.
대신, 본 논문에서는 k=30k=30으로 제한하여, 좌표 상 거리가 가장 가까운 30개의 이웃들과의 관계만 고려한다.
다만, encoder, decoder 모두 3번 message passing을 하기 때문에 더 멀리 있는 (정확하게는 3-hop 관계에 있는) 이웃들의 정보도 보게 되기는 한다.

Details

Autoregressive decomposition
아미노산을 하나씩 예측할까 아니면 한 번에 다 예측할까?
본 논문에서는 decoding 시 아미노산을 하나씩 예측하는 autoregressive sequence prediction을 수행한다. 즉, 3D 구조적인 정보와 이전 아미노산을 참고하여, 다음 아미노산을 하나씩 예측한다. 이를 수식으로 표현하면 아래와 같다.
p(s∣x)=∏ip(si∣x,s<i)p(\mathbf{s}|\mathbf{x}) = \prod_i p(s_i | \mathbf{x}, \mathbf{s}_{<i})
이때, decoder가 받는 input을 다시 살펴보면,
•
(refined) node embedding
Encoder로부터 refine된 node embedding을 의미한다.
•
edge embedding (of k-nearest neighbors)
거리 기준으로 가장 가까운 k개의 이웃들의 구조적인 정보를 담은 edge embedding 이다.
•
sequence embedding (teacher forced)
현재 예측하고자 하는 서열 직전까지의 아미노산 정보만 사용한다.
또한, teacher forcing으로 들어간다. 즉, tt번째 아미노산을 모델이 잘못 예측했다고 하더라도 t+1t+1번째 아미노산을 예측할 때는 tt번째 아미노산의 정답을 사용한다.
Encoder
각 node feature viv_i는 먼저 initial embedding으로 변환된다. hi=Wh(vi)h_{i} = W_h(v_i)
Encoder의 각 layer는 multi-head self-attention을 수행한다.
Query: node ii의 현재 embedding
qi(l)=Wq(l)(hi,in(l))q^{(l)}_i = W^{(l)}_q(h^{(l)}_{i, \text{in}})
Key, value: node ii와 이웃 node jj의 relational information rij(l)=(hj,in(l),eij)r^{(l)}_{ij} = (h^{(l)}_{j, \text{in}}, e_{ij})
kij(l)=Wk(l)(rij(l)),vij(l)=Wv(l)(rij(l))k^{(l)}_{ij} = W^{(l)}_k (r^{(l)}_{ij}), v^{(l)}_{ij} = W^{(l)}_v (r^{(l)}_{ij})
Attention aa 계산
aij(l)=exp⁡(mij(l))∑j′∈N(i,k)exp⁡(mij′(l)), where mij(l)=qi(l)⊤kij(l)da^{(l)}_{ij} = \frac{\exp(m^{(l)}_{ij})}{\sum_{j' \in N(i,k)}\exp(m^{(l)}_{ij'})}, \text{ where } m^{(l)}_{ij} = \frac{{q^{(l)}_{i}}^\top k^{(l)}_{ij}}{\sqrt{d}}
각 attention head ll에서 얻는 weighted sum 형태의 embedding
hi(l)=∑j∈N(i,k)aij(l)vij(l)h^{(l)}_i = \sum_{j \in N(i,k)}a^{(l)}_{ij} v^{(l)}_{ij}
각 attention 이후 output으로 나오는 최종 refined node embedding
hi,out(l)=Wo(hi,in(l)+hi(l))h^{(l)}_{i, \text{out}} = W_o (h^{(l)}_{i, \text{in}} + h^{(l)}_i)
Decoder
Encoder와 동일한 구조이지만, 현재 예측하고자 하는 아미노산 앞부분까지의 서열 정보를 추가로 가지고 있는 relational information 을 사용한다.
rij(l,dec)={(hj(l,dec),eij,g(sj))if i>j(hj(enc),eij,0)if i≤jr^{(l,\text{dec})}_{ij} = \begin{cases} (h^{(l,\text{dec})}_j, e_{ij}, g(s_j)) & \text{if }i > j \\ (h^{\text{(enc)}}_j, e_{ij}, 0) & \text{if } i \leq j \end{cases}
•
hj(l,dec)h^{(l,\text{dec})}_j: 현재 decoder layer의 node jj의 embedding
•
hj(enc)h^{\text{(enc)}}_j: encoder의 모든 layer를 통과한 후의 node jj의 embedding
•
g(sj)g(s_j): 아미노산 sjs_j의 embedding (nn.Embedding)

4. Dataset split: CATH 4.2 split

Inverse folding에 적합한 data split은 무엇일까?
저자들은 CATH hierarchical classification에 의하여, 다음과 같이 구조 기반으로 서열 데이터를 split 하였다.
1.
각 단백질 chain 중 길이 (아미노산 수) 500 이하인 것들만 남긴다.
2.
각 chain의 CAT code를 이용해 train:validation:test = 80:10:10 으로 나눈다.
3.
각 chain이 여러 CAT code를 지닐 수 있기에, train, validation set에서 redundant entry는 없앤다.
4.
Test set에서 train set의 CAT code와 overlap 있는 것들은 지운다.
5.
Validation set에서 train set 및 test set의 CAT code와 overlap 있는 것들은 지운다.

5. Results

Perplexity를 계산했을 때, 기존 구조 기반의 모델 SPIN2 나 language 기반의 모델들보다 훨씬 좋은 성능을 보였다.

Take aways

•
Inverse folding: 구조를 기반으로 서열을 어느 정도 맞출 수 있다!
•
성능 평가 방법을 perplexity로 측정할 수는 있으나, 서열이 달라도 비슷한 구조가 나올 수 있기 때문에 완벽한 metric은 아니다.
•
Inverse folding에는 local environment (거리 기반 k-nearest neighbor)가 중요하다.
•
CATH를 기반으로 dataset을 split 할 수 있다.
Model architecture를 아래와 같이 좀 더 자세히 표현할 수 있다.
StructuredTransformer.pptx
146.4KB